Spatial-aware decision-making with ring attractors in reinforcement learning systems

This paper explores the integration of ring attractors, a mathematical model inspired by neural circuit dynamics, into the reinforcement learning (RL) action selection process. Ring attractors, as specialized brain-inspired structures that encode spatial information and uncertainty, offer a biologically plausible mechanism to improve learning speed and predictive performance. They do so by explicitly encoding the action space, facilitating the organization of neural activity, and enabling the distribution of spatial representations across the neural network in the context of deep RL. The application of ring attractors in the RL action selection process involves mapping actions to specific locations on the ring and decoding the selected action based on neural activity. We investigate the application of ring attractors by both building them as exogenous models and integrating them as part of a Deep Learning policy algorithm. Our results show a significant improvement in state-of-the-art models for the Atari 100k benchmark. Notably, our integrated approach improves the performance of state-of-the-art models by half, representing a 53\% increase over selected baselines.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

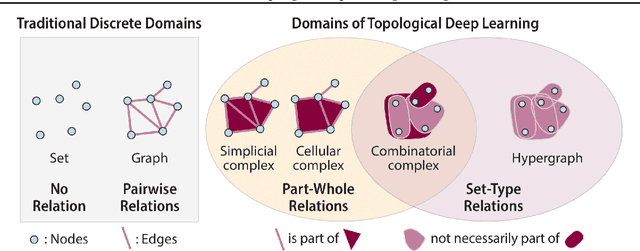
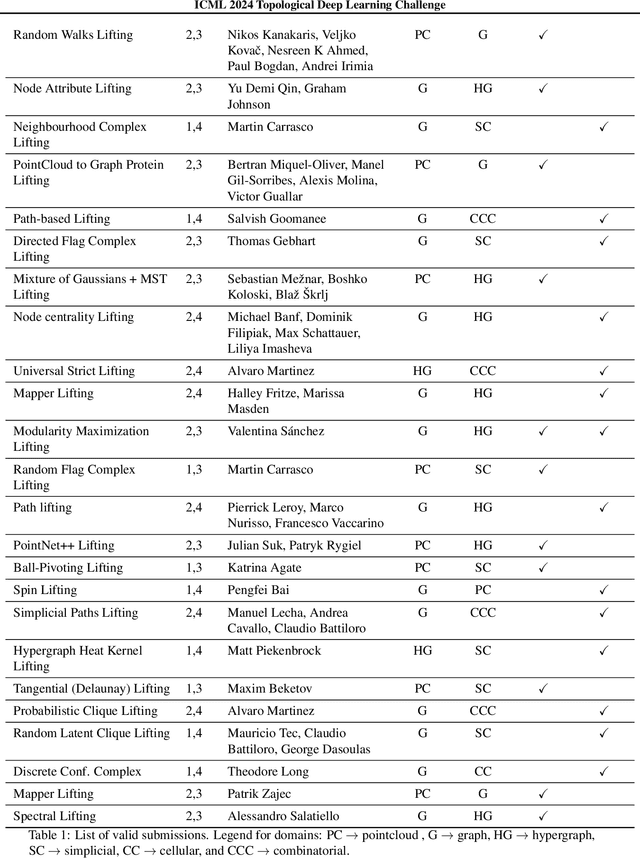
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

TopoBenchmarkX: A Framework for Benchmarking Topological Deep Learning

This work introduces TopoBenchmarkX, a modular open-source library designed to standardize benchmarking and accelerate research in Topological Deep Learning (TDL). TopoBenchmarkX maps the TDL pipeline into a sequence of independent and modular components for data loading and processing, as well as model training, optimization, and evaluation. This modular organization provides flexibility for modifications and facilitates the adaptation and optimization of various TDL pipelines. A key feature of TopoBenchmarkX is that it allows for the transformation and lifting between topological domains. This enables, for example, to obtain richer data representations and more fine-grained analyses by mapping the topology and features of a graph to higher-order topological domains such as simplicial and cell complexes. The range of applicability of TopoBenchmarkX is demonstrated by benchmarking several TDL architectures for various tasks and datasets.

Position Paper: Challenges and Opportunities in Topological Deep Learning

Topological deep learning (TDL) is a rapidly evolving field that uses topological features to understand and design deep learning models. This paper posits that TDL may complement graph representation learning and geometric deep learning by incorporating topological concepts, and can thus provide a natural choice for various machine learning settings. To this end, this paper discusses open problems in TDL, ranging from practical benefits to theoretical foundations. For each problem, it outlines potential solutions and future research opportunities. At the same time, this paper serves as an invitation to the scientific community to actively participate in TDL research to unlock the potential of this emerging field.

TopoX: A Suite of Python Packages for Machine Learning on Topological Domains

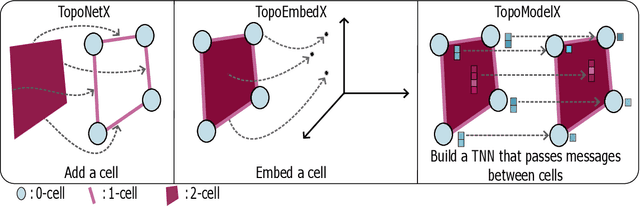
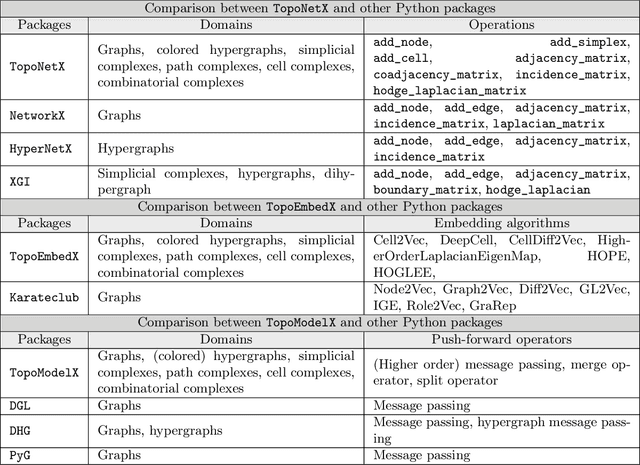
We introduce topox, a Python software suite that provides reliable and user-friendly building blocks for computing and machine learning on topological domains that extend graphs: hypergraphs, simplicial, cellular, path and combinatorial complexes. topox consists of three packages: toponetx facilitates constructing and computing on these domains, including working with nodes, edges and higher-order cells; topoembedx provides methods to embed topological domains into vector spaces, akin to popular graph-based embedding algorithms such as node2vec; topomodelx is built on top of PyTorch and offers a comprehensive toolbox of higher-order message passing functions for neural networks on topological domains. The extensively documented and unit-tested source code of topox is available under MIT license at https://github.com/pyt-team.

Position Paper: Bayesian Deep Learning in the Age of Large-Scale AI

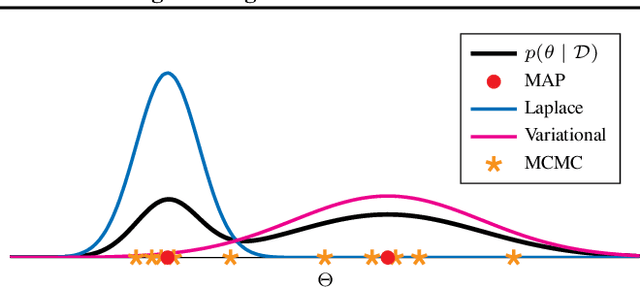
In the current landscape of deep learning research, there is a predominant emphasis on achieving high predictive accuracy in supervised tasks involving large image and language datasets. However, a broader perspective reveals a multitude of overlooked metrics, tasks, and data types, such as uncertainty, active and continual learning, and scientific data, that demand attention. Bayesian deep learning (BDL) constitutes a promising avenue, offering advantages across these diverse settings. This paper posits that BDL can elevate the capabilities of deep learning. It revisits the strengths of BDL, acknowledges existing challenges, and highlights some exciting research avenues aimed at addressing these obstacles. Looking ahead, the discussion focuses on possible ways to combine large-scale foundation models with BDL to unlock their full potential.

Connecting the Dots: Is Mode-Connectedness the Key to Feasible Sample-Based Inference in Bayesian Neural Networks?

A major challenge in sample-based inference (SBI) for Bayesian neural networks is the size and structure of the networks' parameter space. Our work shows that successful SBI is possible by embracing the characteristic relationship between weight and function space, uncovering a systematic link between overparameterization and the difficulty of the sampling problem. Through extensive experiments, we establish practical guidelines for sampling and convergence diagnosis. As a result, we present a Bayesian deep ensemble approach as an effective solution with competitive performance and uncertainty quantification.

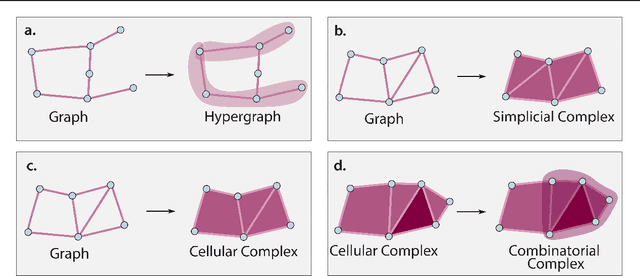
Combinatorial Complexes: Bridging the Gap Between Cell Complexes and Hypergraphs

Graph-based signal processing techniques have become essential for handling data in non-Euclidean spaces. However, there is a growing awareness that these graph models might need to be expanded into `higher-order' domains to effectively represent the complex relations found in high-dimensional data. Such higher-order domains are typically modeled either as hypergraphs, or as simplicial, cubical or other cell complexes. In this context, cell complexes are often seen as a subclass of hypergraphs with additional algebraic structure that can be exploited, e.g., to develop a spectral theory. In this article, we promote an alternative perspective. We argue that hypergraphs and cell complexes emphasize \emph{different} types of relations, which may have different utility depending on the application context. Whereas hypergraphs are effective in modeling set-type, multi-body relations between entities, cell complexes provide an effective means to model hierarchical, interior-to-boundary type relations. We discuss the relative advantages of these two choices and elaborate on the previously introduced concept of a combinatorial complex that enables co-existing set-type and hierarchical relations. Finally, we provide a brief numerical experiment to demonstrate that this modelling flexibility can be advantageous in learning tasks.

Model-agnostic variable importance for predictive uncertainty: an entropy-based approach

In order to trust the predictions of a machine learning algorithm, it is necessary to understand the factors that contribute to those predictions. In the case of probabilistic and uncertainty-aware models, it is necessary to understand not only the reasons for the predictions themselves, but also the model's level of confidence in those predictions. In this paper, we show how existing methods in explainability can be extended to uncertainty-aware models and how such extensions can be used to understand the sources of uncertainty in a model's predictive distribution. In particular, by adapting permutation feature importance, partial dependence plots, and individual conditional expectation plots, we demonstrate that novel insights into model behaviour may be obtained and that these methods can be used to measure the impact of features on both the entropy of the predictive distribution and the log-likelihood of the ground truth labels under that distribution. With experiments using both synthetic and real-world data, we demonstrate the utility of these approaches in understanding both the sources of uncertainty and their impact on model performance.

ICML 2023 Topological Deep Learning Challenge : Design and Results

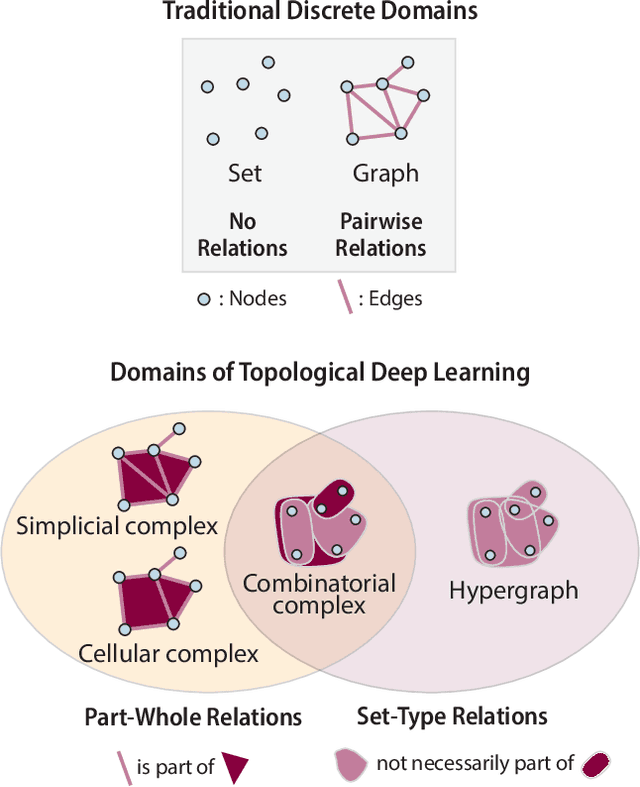
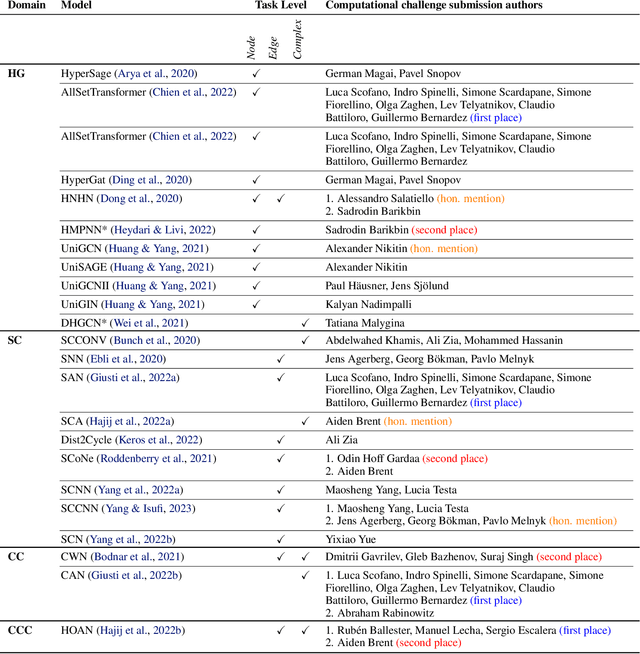
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.