multiGradICON: A Foundation Model for Multimodal Medical Image Registration

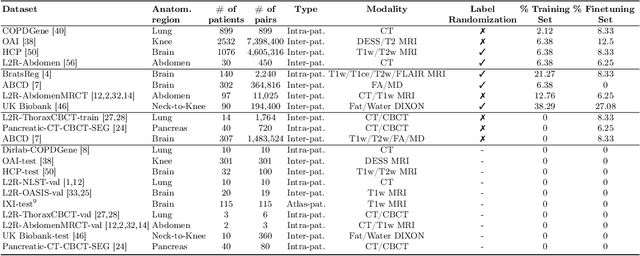
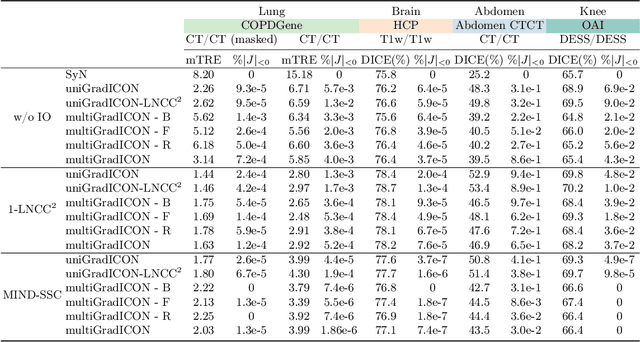
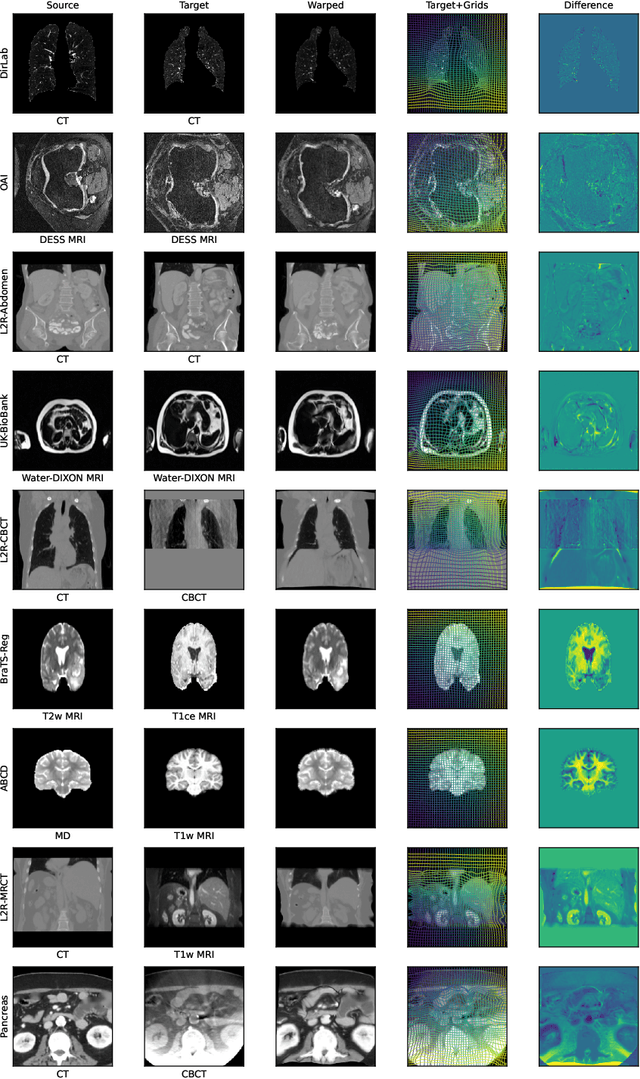
Modern medical image registration approaches predict deformations using deep networks. These approaches achieve state-of-the-art (SOTA) registration accuracy and are generally fast. However, deep learning (DL) approaches are, in contrast to conventional non-deep-learning-based approaches, anatomy-specific. Recently, a universal deep registration approach, uniGradICON, has been proposed. However, uniGradICON focuses on monomodal image registration. In this work, we therefore develop multiGradICON as a first step towards universal *multimodal* medical image registration. Specifically, we show that 1) we can train a DL registration model that is suitable for monomodal *and* multimodal registration; 2) loss function randomization can increase multimodal registration accuracy; and 3) training a model with multimodal data helps multimodal generalization. Our code and the multiGradICON model are available at https://github.com/uncbiag/uniGradICON.

CARL: A Framework for Equivariant Image Registration

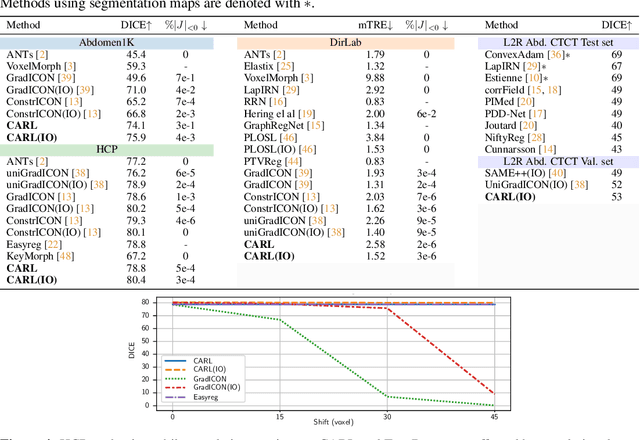
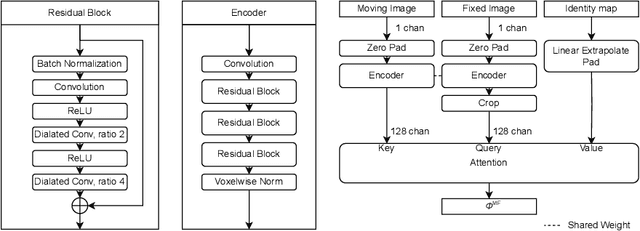
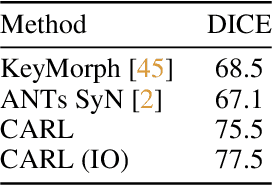
Image registration estimates spatial correspondences between a pair of images. These estimates are typically obtained via numerical optimization or regression by a deep network. A desirable property of such estimators is that a correspondence estimate (e.g., the true oracle correspondence) for an image pair is maintained under deformations of the input images. Formally, the estimator should be equivariant to a desired class of image transformations. In this work, we present careful analyses of the desired equivariance properties in the context of multi-step deep registration networks. Based on these analyses we 1) introduce the notions of $[U,U]$ equivariance (network equivariance to the same deformations of the input images) and $[W,U]$ equivariance (where input images can undergo different deformations); we 2) show that in a suitable multi-step registration setup it is sufficient for overall $[W,U]$ equivariance if the first step has $[W,U]$ equivariance and all others have $[U,U]$ equivariance; we 3) show that common displacement-predicting networks only exhibit $[U,U]$ equivariance to translations instead of the more powerful $[W,U]$ equivariance; and we 4) show how to achieve multi-step $[W,U]$ equivariance via a coordinate-attention mechanism combined with displacement-predicting refinement layers (CARL). Overall, our approach obtains excellent practical registration performance on several 3D medical image registration tasks and outperforms existing unsupervised approaches for the challenging problem of abdomen registration.

Neural Persistence Dynamics

We consider the problem of learning the dynamics in the topology of time-evolving point clouds, the prevalent spatiotemporal model for systems exhibiting collective behavior, such as swarms of insects and birds or particles in physics. In such systems, patterns emerge from (local) interactions among self-propelled entities. While several well-understood governing equations for motion and interaction exist, they are difficult to fit to data due to the often large number of entities and missing correspondences between the observation times, which may also not be equidistant. To evade such confounding factors, we investigate collective behavior from a \textit{topological perspective}, but instead of summarizing entire observation sequences (as in prior work), we propose learning a latent dynamical model from topological features \textit{per time point}. The latter is then used to formulate a downstream regression task to predict the parametrization of some a priori specified governing equation. We implement this idea based on a latent ODE learned from vectorized (static) persistence diagrams and show that this modeling choice is justified by a combination of recent stability results for persistent homology. Various (ablation) experiments not only demonstrate the relevance of each individual model component, but provide compelling empirical evidence that our proposed model -- \textit{neural persistence dynamics} -- substantially outperforms the state-of-the-art across a diverse set of parameter regression tasks.

uniGradICON: A Foundation Model for Medical Image Registration

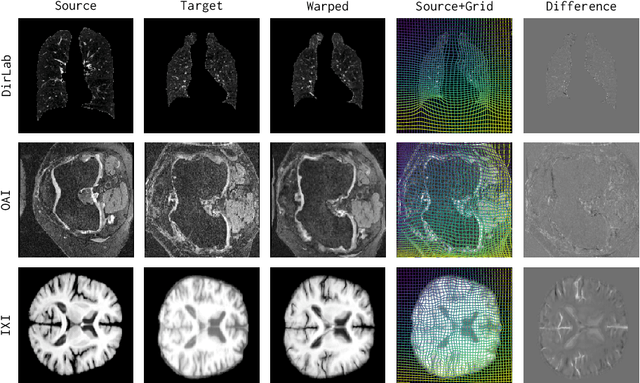
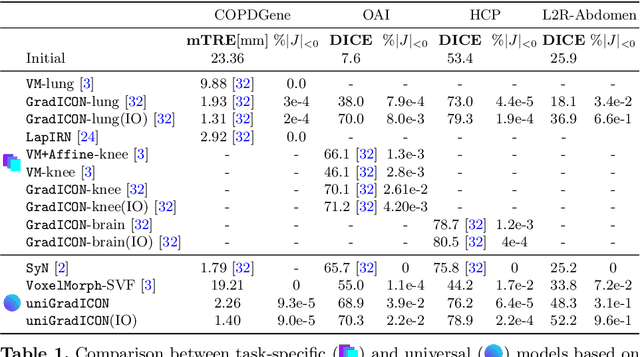
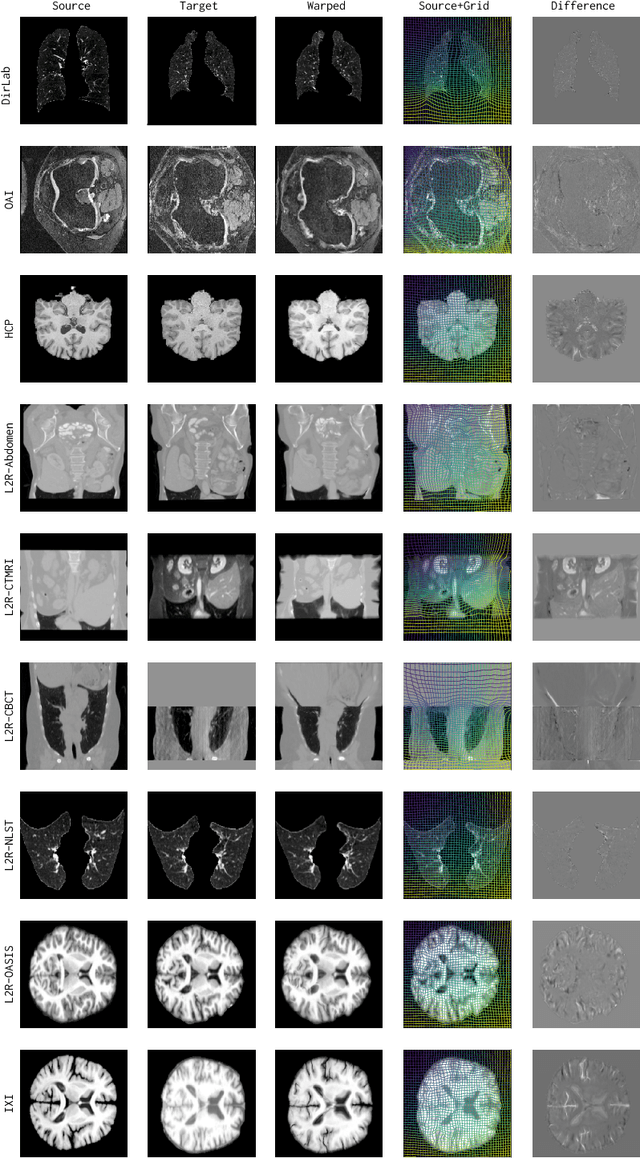
Conventional medical image registration approaches directly optimize over the parameters of a transformation model. These approaches have been highly successful and are used generically for registrations of different anatomical regions. Recent deep registration networks are incredibly fast and accurate but are only trained for specific tasks. Hence, they are no longer generic registration approaches. We therefore propose uniGradICON, a first step toward a foundation model for registration providing 1) great performance \emph{across} multiple datasets which is not feasible for current learning-based registration methods, 2) zero-shot capabilities for new registration tasks suitable for different acquisitions, anatomical regions, and modalities compared to the training dataset, and 3) a strong initialization for finetuning on out-of-distribution registration tasks. UniGradICON unifies the speed and accuracy benefits of learning-based registration algorithms with the generic applicability of conventional non-deep-learning approaches. We extensively trained and evaluated uniGradICON on twelve different public datasets. Our code and the uniGradICON model are available at https://github.com/uncbiag/uniGradICON.

Position Paper: Challenges and Opportunities in Topological Deep Learning

Topological deep learning (TDL) is a rapidly evolving field that uses topological features to understand and design deep learning models. This paper posits that TDL may complement graph representation learning and geometric deep learning by incorporating topological concepts, and can thus provide a natural choice for various machine learning settings. To this end, this paper discusses open problems in TDL, ranging from practical benefits to theoretical foundations. For each problem, it outlines potential solutions and future research opportunities. At the same time, this paper serves as an invitation to the scientific community to actively participate in TDL research to unlock the potential of this emerging field.

Latent SDEs on Homogeneous Spaces

We consider the problem of variational Bayesian inference in a latent variable model where a (possibly complex) observed stochastic process is governed by the solution of a latent stochastic differential equation (SDE). Motivated by the challenges that arise when trying to learn an (almost arbitrary) latent neural SDE from large-scale data, such as efficient gradient computation, we take a step back and study a specific subclass instead. In our case, the SDE evolves on a homogeneous latent space and is induced by stochastic dynamics of the corresponding (matrix) Lie group. In learning problems, SDEs on the unit $n$-sphere are arguably the most relevant incarnation of this setup. Notably, for variational inference, the sphere not only facilitates using a truly uninformative prior SDE, but we also obtain a particularly simple and intuitive expression for the Kullback-Leibler divergence between the approximate posterior and prior process in the evidence lower bound. Experiments demonstrate that a latent SDE of the proposed type can be learned efficiently by means of an existing one-step geometric Euler-Maruyama scheme. Despite restricting ourselves to a less diverse class of SDEs, we achieve competitive or even state-of-the-art performance on various time series interpolation and classification benchmarks.

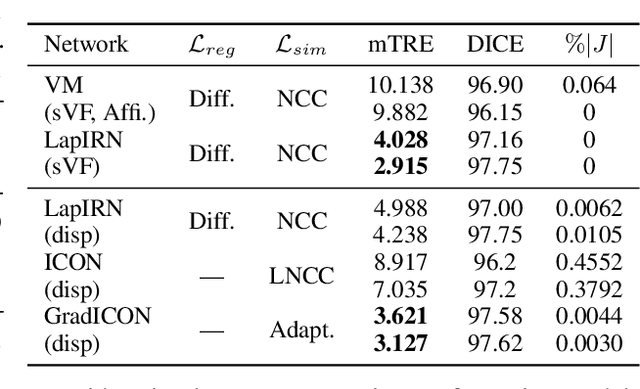
Inverse Consistency by Construction for Multistep Deep Registration

Inverse consistency is a desirable property for image registration. We propose a simple technique to make a neural registration network inverse consistent by construction, as a consequence of its structure, as long as it parameterizes its output transform by a Lie group. We extend this technique to multi-step neural registration by composing many such networks in a way that preserves inverse consistency. This multi-step approach also allows for inverse-consistent coarse to fine registration. We evaluate our technique on synthetic 2-D data and four 3-D medical image registration tasks and obtain excellent registration accuracy while assuring inverse consistency.

GradICON: Approximate Diffeomorphisms via Gradient Inverse Consistency

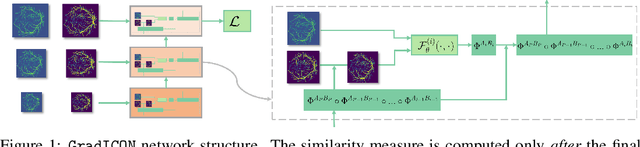
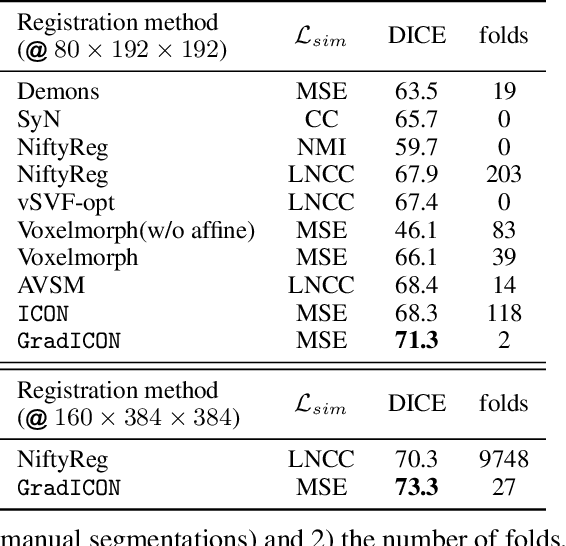
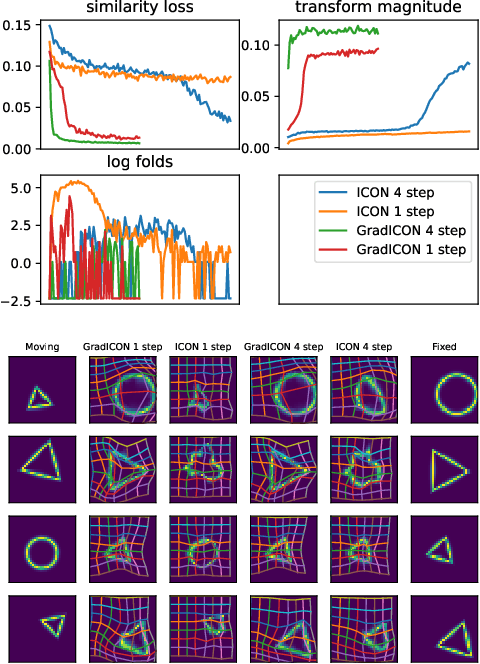
Many registration approaches exist with early work focusing on optimization-based approaches for image pairs. Recent work focuses on deep registration networks to predict spatial transformations. In both cases, commonly used non-parametric registration models, which estimate transformation functions instead of low-dimensional transformation parameters, require choosing a suitable regularizer (to encourage smooth transformations) and its parameters. This makes models difficult to tune and restricts deformations to the deformation space permissible by the chosen regularizer. While deep-learning models for optical flow exist that do not regularize transformations and instead entirely rely on the data these might not yield diffeomorphic transformations which are desirable for medical image registration. In this work, we therefore develop GradICON building upon the unsupervised ICON deep-learning registration approach, which only uses inverse-consistency for regularization. However, in contrast to ICON, we prove and empirically verify that using a gradient inverse-consistency loss not only significantly improves convergence, but also results in a similar implicit regularization of the resulting transformation map. Synthetic experiments and experiments on magnetic resonance (MR) knee images and computed tomography (CT) lung images show the excellent performance of GradICON. We achieve state-of-the-art (SOTA) accuracy while retaining a simple registration formulation, which is practically important.

On Measuring Excess Capacity in Neural Networks

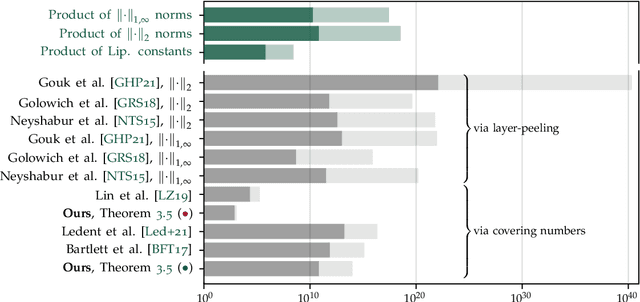
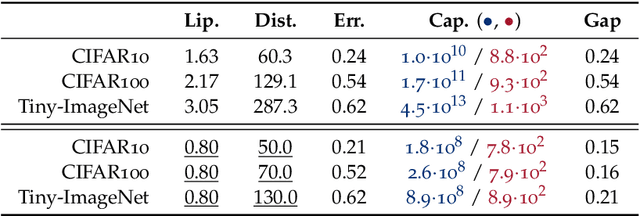
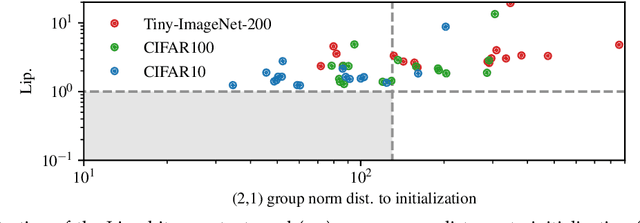
We study the excess capacity of deep networks in the context of supervised classification. That is, given a capacity measure of the underlying hypothesis class -- in our case, Rademacher complexity -- how much can we (a-priori) constrain this class while maintaining an empirical error comparable to the unconstrained setting. To assess excess capacity in modern architectures, we first extend an existing generalization bound to accommodate function composition and addition, as well as the specific structure of convolutions. This then facilitates studying residual networks through the lens of the accompanying capacity measure. The key quantities driving this measure are the Lipschitz constants of the layers and the (2,1) group norm distance to the initializations of the convolution weights. We show that these quantities (1) can be kept surprisingly small and, (2) since excess capacity unexpectedly increases with task difficulty, this points towards an unnecessarily large capacity of unconstrained models.

Comparing object recognition in humans and deep convolutional neural networks -- An eye tracking study

Deep convolutional neural networks (DCNNs) and the ventral visual pathway share vast architectural and functional similarities in visual challenges such as object recognition. Recent insights have demonstrated that both hierarchical cascades can be compared in terms of both exerted behavior and underlying activation. However, these approaches ignore key differences in spatial priorities of information processing. In this proof-of-concept study, we demonstrate a comparison of human observers (N = 45) and three feedforward DCNNs through eye tracking and saliency maps. The results reveal fundamentally different resolutions in both visualization methods that need to be considered for an insightful comparison. Moreover, we provide evidence that a DCNN with biologically plausible receptive field sizes called vNet reveals higher agreement with human viewing behavior as contrasted with a standard ResNet architecture. We find that image-specific factors such as category, animacy, arousal, and valence have a direct link to the agreement of spatial object recognition priorities in humans and DCNNs, while other measures such as difficulty and general image properties do not. With this approach, we try to open up new perspectives at the intersection of biological and computer vision research.