Semi-Discrete Optimal Transport: Nearly Minimax Estimation With Stochastic Gradient Descent and Adaptive Entropic Regularization

Optimal Transport (OT) based distances are powerful tools for machine learning to compare probability measures and manipulate them using OT maps. In this field, a setting of interest is semi-discrete OT, where the source measure $\mu$ is continuous, while the target $\nu$ is discrete. Recent works have shown that the minimax rate for the OT map is $\mathcal{O}(t^{-1/2})$ when using $t$ i.i.d. subsamples from each measure (two-sample setting). An open question is whether a better convergence rate can be achieved when the full information of the discrete measure $\nu$ is known (one-sample setting). In this work, we answer positively to this question by (i) proving an $\mathcal{O}(t^{-1})$ lower bound rate for the OT map, using the similarity between Laguerre cells estimation and density support estimation, and (ii) proposing a Stochastic Gradient Descent (SGD) algorithm with adaptive entropic regularization and averaging acceleration. To nearly achieve the desired fast rate, characteristic of non-regular parametric problems, we design an entropic regularization scheme decreasing with the number of samples. Another key step in our algorithm consists of using a projection step that permits to leverage the local strong convexity of the regularized OT problem. Our convergence analysis integrates online convex optimization and stochastic gradient techniques, complemented by the specificities of the OT semi-dual. Moreover, while being as computationally and memory efficient as vanilla SGD, our algorithm achieves the unusual fast rates of our theory in numerical experiments.

Understanding the training of infinitely deep and wide ResNets with Conditional Optimal Transport

We study the convergence of gradient flow for the training of deep neural networks. If Residual Neural Networks are a popular example of very deep architectures, their training constitutes a challenging optimization problem due notably to the non-convexity and the non-coercivity of the objective. Yet, in applications, those tasks are successfully solved by simple optimization algorithms such as gradient descent. To better understand this phenomenon, we focus here on a ``mean-field'' model of infinitely deep and arbitrarily wide ResNet, parameterized by probability measures over the product set of layers and parameters and with constant marginal on the set of layers. Indeed, in the case of shallow neural networks, mean field models have proven to benefit from simplified loss-landscapes and good theoretical guarantees when trained with gradient flow for the Wasserstein metric on the set of probability measures. Motivated by this approach, we propose to train our model with gradient flow w.r.t. the conditional Optimal Transport distance: a restriction of the classical Wasserstein distance which enforces our marginal condition. Relying on the theory of gradient flows in metric spaces we first show the well-posedness of the gradient flow equation and its consistency with the training of ResNets at finite width. Performing a local Polyak-\L{}ojasiewicz analysis, we then show convergence of the gradient flow for well-chosen initializations: if the number of features is finite but sufficiently large and the risk is sufficiently small at initialization, the gradient flow converges towards a global minimizer. This is the first result of this type for infinitely deep and arbitrarily wide ResNets.

Unbalanced Optimal Transport, from Theory to Numerics

Optimal Transport (OT) has recently emerged as a central tool in data sciences to compare in a geometrically faithful way point clouds and more generally probability distributions. The wide adoption of OT into existing data analysis and machine learning pipelines is however plagued by several shortcomings. This includes its lack of robustness to outliers, its high computational costs, the need for a large number of samples in high dimension and the difficulty to handle data in distinct spaces. In this review, we detail several recently proposed approaches to mitigate these issues. We insist in particular on unbalanced OT, which compares arbitrary positive measures, not restricted to probability distributions (i.e. their total mass can vary). This generalization of OT makes it robust to outliers and missing data. The second workhorse of modern computational OT is entropic regularization, which leads to scalable algorithms while lowering the sample complexity in high dimension. The last point presented in this review is the Gromov-Wasserstein (GW) distance, which extends OT to cope with distributions belonging to different metric spaces. The main motivation for this review is to explain how unbalanced OT, entropic regularization and GW can work hand-in-hand to turn OT into efficient geometric loss functions for data sciences.

GradICON: Approximate Diffeomorphisms via Gradient Inverse Consistency

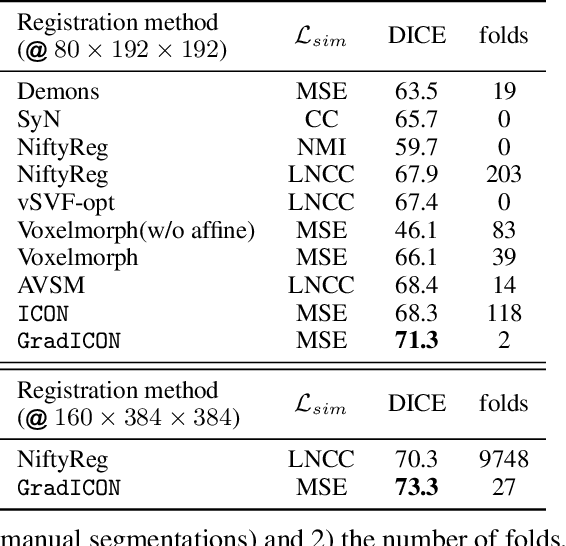
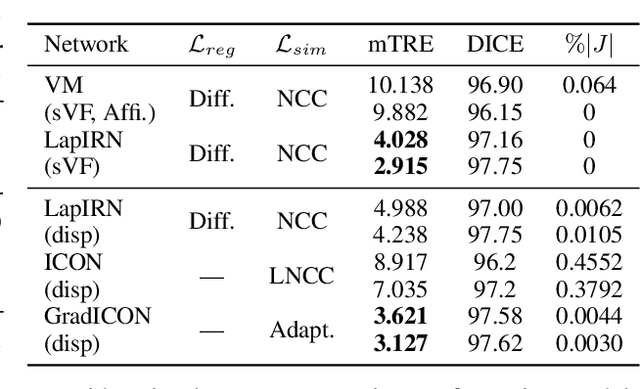
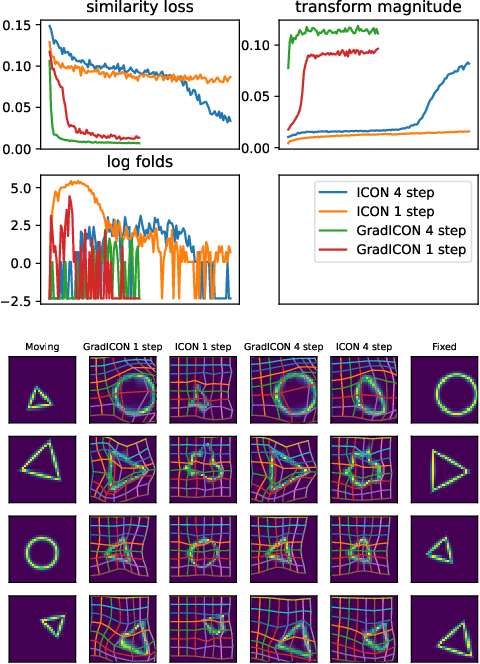
Many registration approaches exist with early work focusing on optimization-based approaches for image pairs. Recent work focuses on deep registration networks to predict spatial transformations. In both cases, commonly used non-parametric registration models, which estimate transformation functions instead of low-dimensional transformation parameters, require choosing a suitable regularizer (to encourage smooth transformations) and its parameters. This makes models difficult to tune and restricts deformations to the deformation space permissible by the chosen regularizer. While deep-learning models for optical flow exist that do not regularize transformations and instead entirely rely on the data these might not yield diffeomorphic transformations which are desirable for medical image registration. In this work, we therefore develop GradICON building upon the unsupervised ICON deep-learning registration approach, which only uses inverse-consistency for regularization. However, in contrast to ICON, we prove and empirically verify that using a gradient inverse-consistency loss not only significantly improves convergence, but also results in a similar implicit regularization of the resulting transformation map. Synthetic experiments and experiments on magnetic resonance (MR) knee images and computed tomography (CT) lung images show the excellent performance of GradICON. We achieve state-of-the-art (SOTA) accuracy while retaining a simple registration formulation, which is practically important.

Toric Geometry of Entropic Regularization

Entropic regularization is a method for large-scale linear programming. Geometrically, one traces intersections of the feasible polytope with scaled toric varieties, starting at the Birch point. We compare this to log-barrier methods, with reciprocal linear spaces, starting at the analytic center. We revisit entropic regularization for unbalanced optimal transport, and we develop the use of optimal conic couplings. We compute the degree of the associated toric variety, and we explore algorithms like iterative scaling.

Faster Unbalanced Optimal Transport: Translation invariant Sinkhorn and 1-D Frank-Wolfe

Unbalanced optimal transport (UOT) extends optimal transport (OT) to take into account mass variations to compare distributions. This is crucial to make OT successful in ML applications, making it robust to data normalization and outliers. The baseline algorithm is Sinkhorn, but its convergence speed might be significantly slower for UOT than for OT. In this work, we identify the cause for this deficiency, namely the lack of a global normalization of the iterates, which equivalently corresponds to a translation of the dual OT potentials. Our first contribution leverages this idea to develop a provably accelerated Sinkhorn algorithm (coined 'translation invariant Sinkhorn') for UOT, bridging the computational gap with OT. Our second contribution focusses on 1-D UOT and proposes a Frank-Wolfe solver applied to this translation invariant formulation. The linear oracle of each steps amounts to solving a 1-D OT problems, resulting in a linear time complexity per iteration. Our last contribution extends this method to the computation of UOT barycenter of 1-D measures. Numerical simulations showcase the convergence speed improvement brought by these three approaches.

Near-optimal estimation of smooth transport maps with kernel sums-of-squares

It was recently shown that under smoothness conditions, the squared Wasserstein distance between two distributions could be efficiently computed with appealing statistical error upper bounds. However, rather than the distance itself, the object of interest for applications such as generative modeling is the underlying optimal transport map. Hence, computational and statistical guarantees need to be obtained for the estimated maps themselves. In this paper, we propose the first tractable algorithm for which the statistical $L^2$ error on the maps nearly matches the existing minimax lower-bounds for smooth map estimation. Our method is based on solving the semi-dual formulation of optimal transport with an infinite-dimensional sum-of-squares reformulation, and leads to an algorithm which has dimension-free polynomial rates in the number of samples, with potentially exponentially dimension-dependent constants.

Global convergence of ResNets: From finite to infinite width using linear parameterization

Overparametrization is a key factor in the absence of convexity to explain global convergence of gradient descent (GD) for neural networks. Beside the well studied lazy regime, infinite width (mean field) analysis has been developed for shallow networks, using on convex optimization technics. To bridge the gap between the lazy and mean field regimes, we study Residual Networks (ResNets) in which the residual block has linear parametrization while still being nonlinear. Such ResNets admit both infinite depth and width limits, encoding residual blocks in a Reproducing Kernel Hilbert Space (RKHS). In this limit, we prove a local Polyak-Lojasiewicz inequality. Thus, every critical point is a global minimizer and a local convergence result of GD holds, retrieving the lazy regime. In contrast with other mean-field studies, it applies to both parametric and non-parametric cases under an expressivity condition on the residuals. Our analysis leads to a practical and quantified recipe: starting from a universal RKHS, Random Fourier Features are applied to obtain a finite dimensional parameterization satisfying with high-probability our expressivity condition.

The Unbalanced Gromov Wasserstein Distance: Conic Formulation and Relaxation

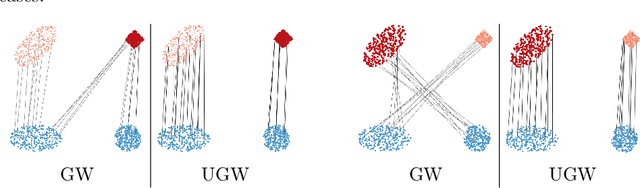
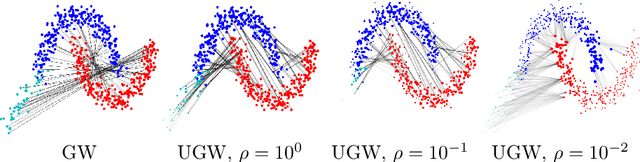
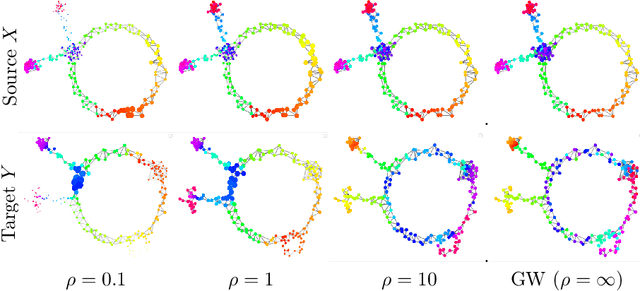
Comparing metric measure spaces (i.e. a metric space endowed with a probability distribution) is at the heart of many machine learning problems. This includes for instance predicting properties of molecules in quantum chemistry or generating graphs with varying connectivity. The most popular distance between such metric measure spaces is the Gromov-Wasserstein (GW) distance, which is the solution of a quadratic assignment problem. This distance has been successfully applied to supervised learning and generative modeling, for applications as diverse as quantum chemistry or natural language processing. The GW distance is however limited to the comparison of metric measure spaces endowed with a \emph{probability} distribution. This strong limitation is problematic for many applications in ML where there is no a priori natural normalization on the total mass of the data. Furthermore, imposing an exact conservation of mass across spaces is not robust to outliers and often leads to irregular matching. To alleviate these issues, we introduce two Unbalanced Gromov-Wasserstein formulations: a distance and a more computationally tractable upper-bounding relaxation. They both allow the comparison of metric spaces equipped with arbitrary positive measures up to isometries.

A Shooting Formulation of Deep Learning

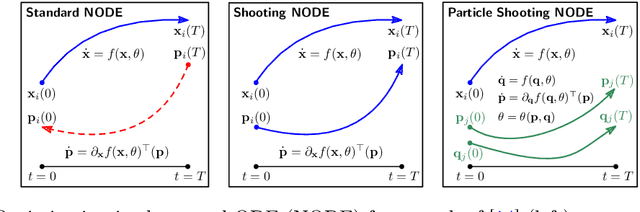
Continuous-depth neural networks can be viewed as deep limits of discrete neural networks whose dynamics resemble a discretization of an ordinary differential equation (ODE). Although important steps have been taken to realize the advantages of such continuous formulations, most current techniques are not truly continuous-depth as they assume identical layers. Indeed, existing works throw into relief the myriad difficulties presented by an infinite-dimensional parameter space in learning a continuous-depth neural ODE. To this end, we introduce a shooting formulation which shifts the perspective from parameterizing a network layer-by-layer to parameterizing over optimal networks described only by a set of initial conditions. For scalability, we propose a novel particle-ensemble parametrization which fully specifies the optimal weight trajectory of the continuous-depth neural network. Our experiments show that our particle-ensemble shooting formulation can achieve competitive performance, especially on long-range forecasting tasks. Finally, though the current work is inspired by continuous-depth neural networks, the particle-ensemble shooting formulation also applies to discrete-time networks and may lead to a new fertile area of research in deep learning parametrization.