The Unbalanced Gromov Wasserstein Distance: Conic Formulation and Relaxation

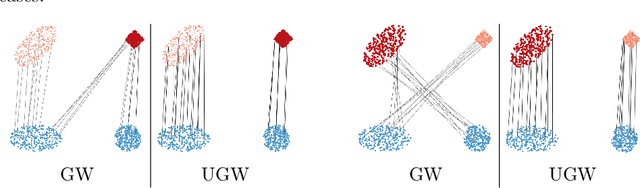
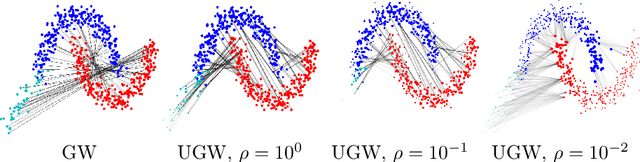
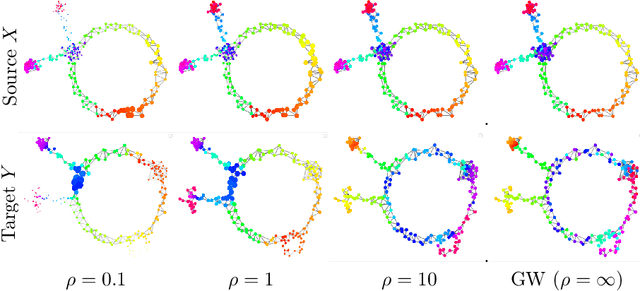
Comparing metric measure spaces (i.e. a metric space endowed with a probability distribution) is at the heart of many machine learning problems. This includes for instance predicting properties of molecules in quantum chemistry or generating graphs with varying connectivity. The most popular distance between such metric measure spaces is the Gromov-Wasserstein (GW) distance, which is the solution of a quadratic assignment problem. This distance has been successfully applied to supervised learning and generative modeling, for applications as diverse as quantum chemistry or natural language processing. The GW distance is however limited to the comparison of metric measure spaces endowed with a \emph{probability} distribution. This strong limitation is problematic for many applications in ML where there is no a priori natural normalization on the total mass of the data. Furthermore, imposing an exact conservation of mass across spaces is not robust to outliers and often leads to irregular matching. To alleviate these issues, we introduce two Unbalanced Gromov-Wasserstein formulations: a distance and a more computationally tractable upper-bounding relaxation. They both allow the comparison of metric spaces equipped with arbitrary positive measures up to isometries.