Leveraging free energy in pretraining model selection for improved fine-tuning

Recent advances in artificial intelligence have been fueled by the development of foundation models such as BERT, GPT, T5, and Vision Transformers. These models are first pretrained on vast and diverse datasets and then adapted to specific downstream tasks, often with significantly less data. However, the mechanisms behind the success of this ubiquitous pretrain-then-adapt paradigm remain underexplored, particularly the characteristics of pretraining checkpoints that lend themselves to good downstream adaptation. We introduce a Bayesian model selection criterion, called the downstream free energy, which quantifies a checkpoint's adaptability by measuring the concentration of nearby favorable parameters for the downstream task. We demonstrate that this free energy criterion can be effectively implemented without access to the downstream data or prior knowledge of the downstream task. Furthermore, we provide empirical evidence that the free energy criterion reliably correlates with improved fine-tuning performance, offering a principled approach to predicting model adaptability.

Temperature Optimization for Bayesian Deep Learning

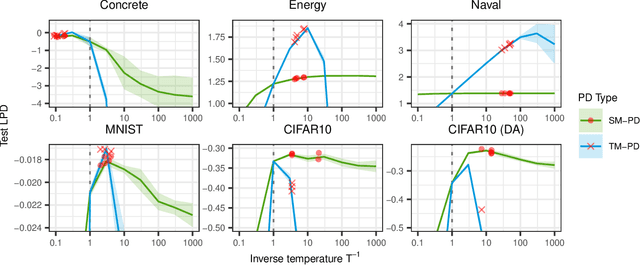
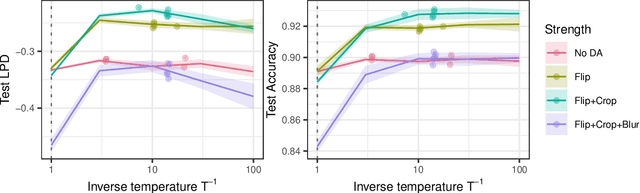
The Cold Posterior Effect (CPE) is a phenomenon in Bayesian Deep Learning (BDL), where tempering the posterior to a cold temperature often improves the predictive performance of the posterior predictive distribution (PPD). Although the term `CPE' suggests colder temperatures are inherently better, the BDL community increasingly recognizes that this is not always the case. Despite this, there remains no systematic method for finding the optimal temperature beyond grid search. In this work, we propose a data-driven approach to select the temperature that maximizes test log-predictive density, treating the temperature as a model parameter and estimating it directly from the data. We empirically demonstrate that our method performs comparably to grid search, at a fraction of the cost, across both regression and classification tasks. Finally, we highlight the differing perspectives on CPE between the BDL and Generalized Bayes communities: while the former primarily focuses on predictive performance of the PPD, the latter emphasizes calibrated uncertainty and robustness to model misspecification; these distinct objectives lead to different temperature preferences.

Pathwise Gradient Variance Reduction with Control Variates in Variational Inference

Variational inference in Bayesian deep learning often involves computing the gradient of an expectation that lacks a closed-form solution. In these cases, pathwise and score-function gradient estimators are the most common approaches. The pathwise estimator is often favoured for its substantially lower variance compared to the score-function estimator, which typically requires variance reduction techniques. However, recent research suggests that even pathwise gradient estimators could benefit from variance reduction. In this work, we review existing control-variates-based variance reduction methods for pathwise gradient estimators to assess their effectiveness. Notably, these methods often rely on integrand approximations and are applicable only to simple variational families. To address this limitation, we propose applying zero-variance control variates to pathwise gradient estimators. This approach offers the advantage of requiring minimal assumptions about the variational distribution, other than being able to sample from it.

The Developmental Landscape of In-Context Learning

We show that in-context learning emerges in transformers in discrete developmental stages, when they are trained on either language modeling or linear regression tasks. We introduce two methods for detecting the milestones that separate these stages, by probing the geometry of the population loss in both parameter space and function space. We study the stages revealed by these new methods using a range of behavioral and structural metrics to establish their validity.

Interventional Fairness on Partially Known Causal Graphs: A Constrained Optimization Approach

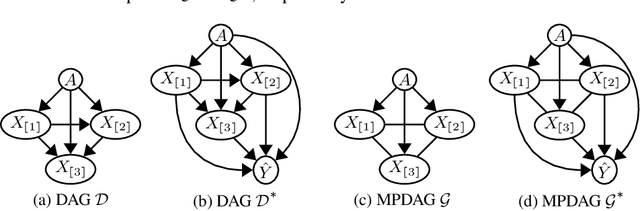
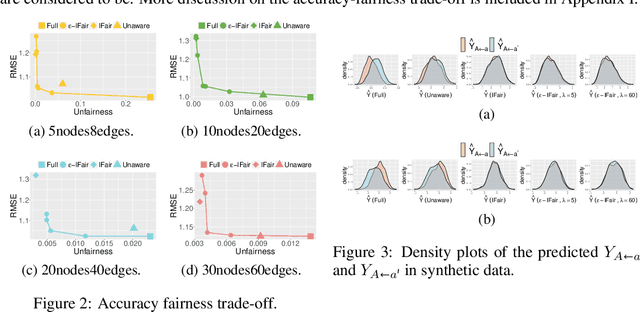
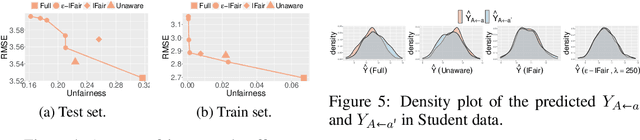
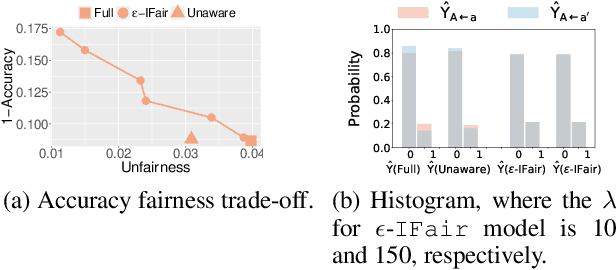
Fair machine learning aims to prevent discrimination against individuals or sub-populations based on sensitive attributes such as gender and race. In recent years, causal inference methods have been increasingly used in fair machine learning to measure unfairness by causal effects. However, current methods assume that the true causal graph is given, which is often not true in real-world applications. To address this limitation, this paper proposes a framework for achieving causal fairness based on the notion of interventions when the true causal graph is partially known. The proposed approach involves modeling fair prediction using a Partially Directed Acyclic Graph (PDAG), specifically, a class of causal DAGs that can be learned from observational data combined with domain knowledge. The PDAG is used to measure causal fairness, and a constrained optimization problem is formulated to balance between fairness and accuracy. Results on both simulated and real-world datasets demonstrate the effectiveness of this method.

Dynamical versus Bayesian Phase Transitions in a Toy Model of Superposition

We investigate phase transitions in a Toy Model of Superposition (TMS) using Singular Learning Theory (SLT). We derive a closed formula for the theoretical loss and, in the case of two hidden dimensions, discover that regular $k$-gons are critical points. We present supporting theory indicating that the local learning coefficient (a geometric invariant) of these $k$-gons determines phase transitions in the Bayesian posterior as a function of training sample size. We then show empirically that the same $k$-gon critical points also determine the behavior of SGD training. The picture that emerges adds evidence to the conjecture that the SGD learning trajectory is subject to a sequential learning mechanism. Specifically, we find that the learning process in TMS, be it through SGD or Bayesian learning, can be characterized by a journey through parameter space from regions of high loss and low complexity to regions of low loss and high complexity.

Quantifying degeneracy in singular models via the learning coefficient

Deep neural networks (DNN) are singular statistical models which exhibit complex degeneracies. In this work, we illustrate how a quantity known as the \emph{learning coefficient} introduced in singular learning theory quantifies precisely the degree of degeneracy in deep neural networks. Importantly, we will demonstrate that degeneracy in DNN cannot be accounted for by simply counting the number of "flat" directions. We propose a computationally scalable approximation of a localized version of the learning coefficient using stochastic gradient Langevin dynamics. To validate our approach, we demonstrate its accuracy in low-dimensional models with known theoretical values. Importantly, the local learning coefficient can correctly recover the ordering of degeneracy between various parameter regions of interest. An experiment on MNIST shows the local learning coefficient can reveal the inductive bias of stochastic opitmizers for more or less degenerate critical points.

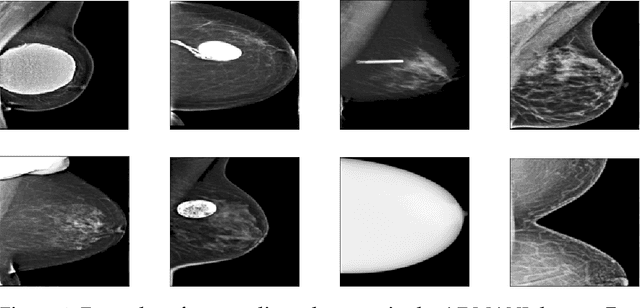
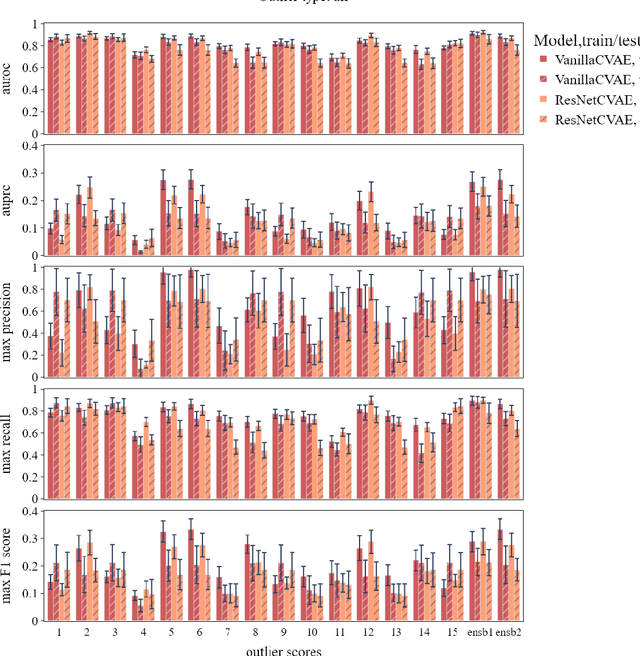
Technical outlier detection via convolutional variational autoencoder for the ADMANI breast mammogram dataset

The ADMANI datasets (annotated digital mammograms and associated non-image datasets) from the Transforming Breast Cancer Screening with AI programme (BRAIx) run by BreastScreen Victoria in Australia are multi-centre, large scale, clinically curated, real-world databases. The datasets are expected to aid in the development of clinically relevant Artificial Intelligence (AI) algorithms for breast cancer detection, early diagnosis, and other applications. To ensure high data quality, technical outliers must be removed before any downstream algorithm development. As a first step, we randomly select 30,000 individual mammograms and use Convolutional Variational Autoencoder (CVAE), a deep generative neural network, to detect outliers. CVAE is expected to detect all sorts of outliers, although its detection performance differs among different types of outliers. Traditional image processing techniques such as erosion and pectoral muscle analysis can compensate for the poor performance of CVAE in certain outlier types. We identify seven types of technical outliers: implant, pacemaker, cardiac loop recorder, improper radiography, atypical lesion/calcification, incorrect exposure parameter and improper placement. The outlier recall rate for the test set is 61% if CVAE, erosion and pectoral muscle analysis each select the top 1% images ranked in ascending or descending order according to image outlier score under each detection method, and 83% if each selects the top 5% images. This study offers an overview of technical outliers in the ADMANI dataset and suggests future directions to improve outlier detection effectiveness.

Variational Bayesian Neural Networks via Resolution of Singularities

In this work, we advocate for the importance of singular learning theory (SLT) as it pertains to the theory and practice of variational inference in Bayesian neural networks (BNNs). To begin, using SLT, we lay to rest some of the confusion surrounding discrepancies between downstream predictive performance measured via e.g., the test log predictive density, and the variational objective. Next, we use the SLT-corrected asymptotic form for singular posterior distributions to inform the design of the variational family itself. Specifically, we build upon the idealized variational family introduced in \citet{bhattacharya_evidence_2020} which is theoretically appealing but practically intractable. Our proposal takes shape as a normalizing flow where the base distribution is a carefully-initialized generalized gamma. We conduct experiments comparing this to the canonical Gaussian base distribution and show improvements in terms of variational free energy and variational generalization error.

Counterfactual Fairness with Partially Known Causal Graph

Fair machine learning aims to avoid treating individuals or sub-populations unfavourably based on \textit{sensitive attributes}, such as gender and race. Those methods in fair machine learning that are built on causal inference ascertain discrimination and bias through causal effects. Though causality-based fair learning is attracting increasing attention, current methods assume the true causal graph is fully known. This paper proposes a general method to achieve the notion of counterfactual fairness when the true causal graph is unknown. To be able to select features that lead to counterfactual fairness, we derive the conditions and algorithms to identify ancestral relations between variables on a \textit{Partially Directed Acyclic Graph (PDAG)}, specifically, a class of causal DAGs that can be learned from observational data combined with domain knowledge. Interestingly, we find that counterfactual fairness can be achieved as if the true causal graph were fully known, when specific background knowledge is provided: the sensitive attributes do not have ancestors in the causal graph. Results on both simulated and real-world datasets demonstrate the effectiveness of our method.