Temperature Optimization for Bayesian Deep Learning

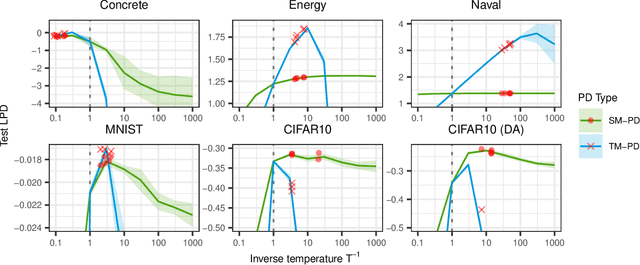
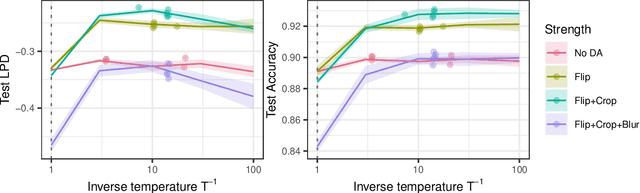
The Cold Posterior Effect (CPE) is a phenomenon in Bayesian Deep Learning (BDL), where tempering the posterior to a cold temperature often improves the predictive performance of the posterior predictive distribution (PPD). Although the term `CPE' suggests colder temperatures are inherently better, the BDL community increasingly recognizes that this is not always the case. Despite this, there remains no systematic method for finding the optimal temperature beyond grid search. In this work, we propose a data-driven approach to select the temperature that maximizes test log-predictive density, treating the temperature as a model parameter and estimating it directly from the data. We empirically demonstrate that our method performs comparably to grid search, at a fraction of the cost, across both regression and classification tasks. Finally, we highlight the differing perspectives on CPE between the BDL and Generalized Bayes communities: while the former primarily focuses on predictive performance of the PPD, the latter emphasizes calibrated uncertainty and robustness to model misspecification; these distinct objectives lead to different temperature preferences.

Gradient-enhanced deep Gaussian processes for multifidelity modelling

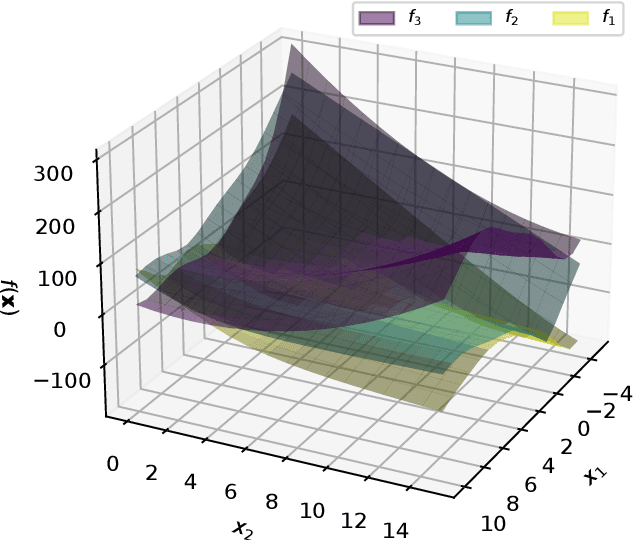
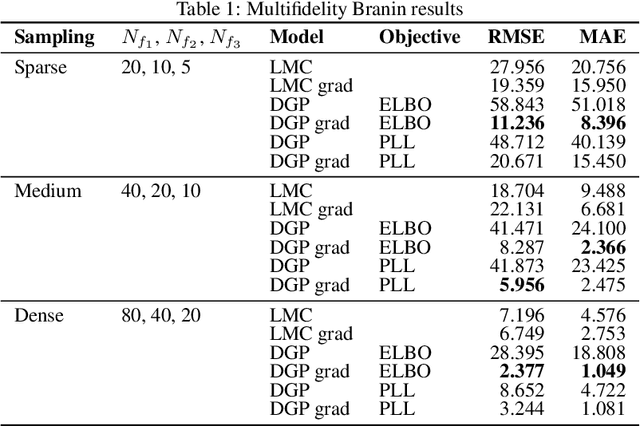
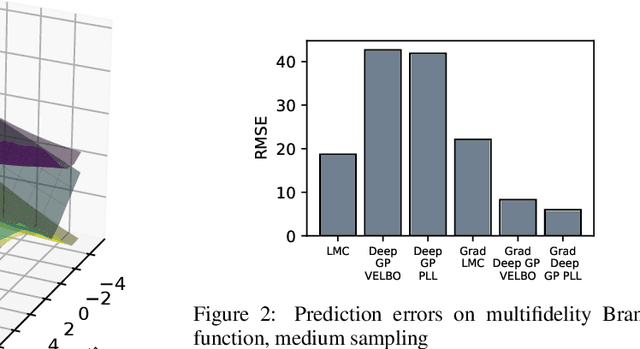
Multifidelity models integrate data from multiple sources to produce a single approximator for the underlying process. Dense low-fidelity samples are used to reduce interpolation error, while sparse high-fidelity samples are used to compensate for bias or noise in the low-fidelity samples. Deep Gaussian processes (GPs) are attractive for multifidelity modelling as they are non-parametric, robust to overfitting, perform well for small datasets, and, critically, can capture nonlinear and input-dependent relationships between data of different fidelities. Many datasets naturally contain gradient data, especially when they are generated by computational models that are compatible with automatic differentiation or have adjoint solutions. Principally, this work extends deep GPs to incorporate gradient data. We demonstrate this method on an analytical test problem and a realistic partial differential equation problem, where we predict the aerodynamic coefficients of a hypersonic flight vehicle over a range of flight conditions and geometries. In both examples, the gradient-enhanced deep GP outperforms a gradient-enhanced linear GP model and their non-gradient-enhanced counterparts.

A PAC-Bayesian Perspective on the Interpolating Information Criterion

Deep learning is renowned for its theory-practice gap, whereby principled theory typically fails to provide much beneficial guidance for implementation in practice. This has been highlighted recently by the benign overfitting phenomenon: when neural networks become sufficiently large to interpolate the dataset perfectly, model performance appears to improve with increasing model size, in apparent contradiction with the well-known bias-variance tradeoff. While such phenomena have proven challenging to theoretically study for general models, the recently proposed Interpolating Information Criterion (IIC) provides a valuable theoretical framework to examine performance for overparameterized models. Using the IIC, a PAC-Bayes bound is obtained for a general class of models, characterizing factors which influence generalization performance in the interpolating regime. From the provided bound, we quantify how the test error for overparameterized models achieving effectively zero training error depends on the quality of the implicit regularization imposed by e.g. the combination of model, optimizer, and parameter-initialization scheme; the spectrum of the empirical neural tangent kernel; curvature of the loss landscape; and noise present in the data.

The Interpolating Information Criterion for Overparameterized Models

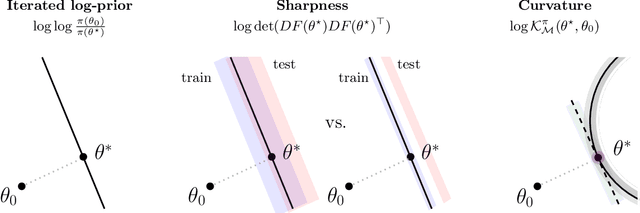
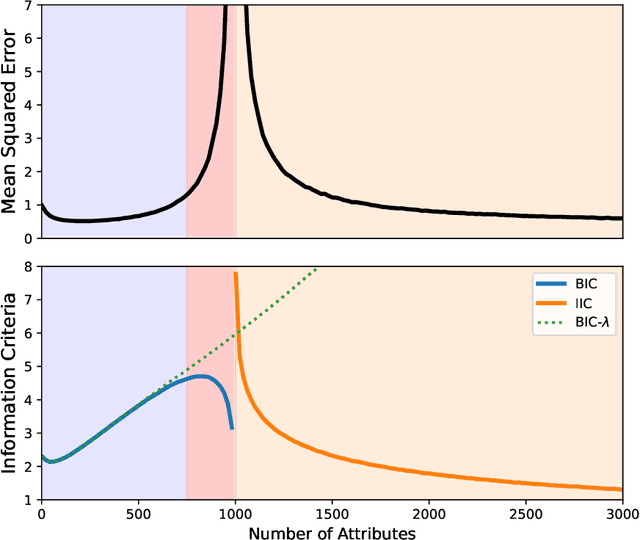
The problem of model selection is considered for the setting of interpolating estimators, where the number of model parameters exceeds the size of the dataset. Classical information criteria typically consider the large-data limit, penalizing model size. However, these criteria are not appropriate in modern settings where overparameterized models tend to perform well. For any overparameterized model, we show that there exists a dual underparameterized model that possesses the same marginal likelihood, thus establishing a form of Bayesian duality. This enables more classical methods to be used in the overparameterized setting, revealing the Interpolating Information Criterion, a measure of model quality that naturally incorporates the choice of prior into the model selection. Our new information criterion accounts for prior misspecification, geometric and spectral properties of the model, and is numerically consistent with known empirical and theoretical behavior in this regime.

Monotonicity and Double Descent in Uncertainty Estimation with Gaussian Processes

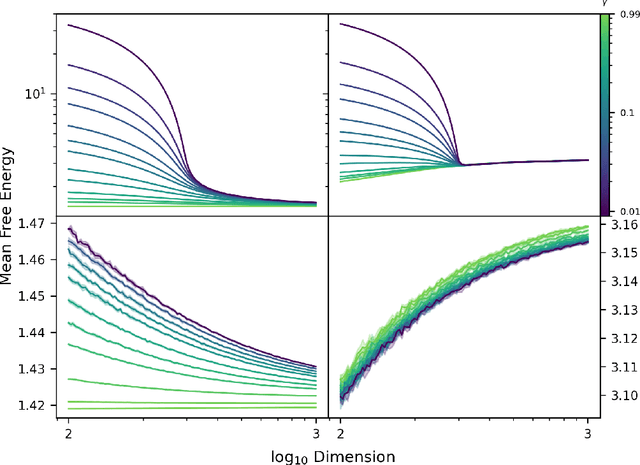
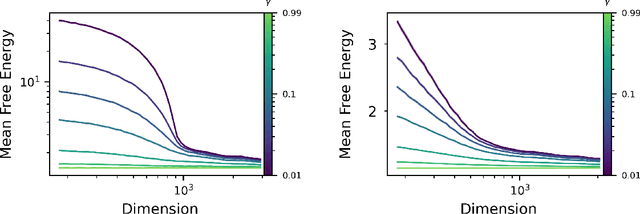
The quality of many modern machine learning models improves as model complexity increases, an effect that has been quantified, for predictive performance, with the non-monotonic double descent learning curve. Here, we address the overarching question: is there an analogous theory of double descent for models which estimate uncertainty? We provide a partially affirmative and partially negative answer in the setting of Gaussian processes (GP). Under standard assumptions, we prove that higher model quality for optimally-tuned GPs (including uncertainty prediction) under marginal likelihood is realized for larger input dimensions, and therefore exhibits a monotone error curve. After showing that marginal likelihood does not naturally exhibit double descent in the input dimension, we highlight related forms of posterior predictive loss that do exhibit non-monotonicity. Finally, we verify empirically that our results hold for real data, beyond our considered assumptions, and we explore consequences involving synthetic covariates.

Stochastic Normalizing Flows

We introduce stochastic normalizing flows, an extension of continuous normalizing flows for maximum likelihood estimation and variational inference (VI) using stochastic differential equations (SDEs). Using the theory of rough paths, the underlying Brownian motion is treated as a latent variable and approximated, enabling efficient training of neural SDEs as random neural ordinary differential equations. These SDEs can be used for constructing efficient Markov chains to sample from the underlying distribution of a given dataset. Furthermore, by considering families of targeted SDEs with prescribed stationary distribution, we can apply VI to the optimization of hyperparameters in stochastic MCMC.