Fred Roosta
Latent Refinement via Flow Matching for Training-free Linear Inverse Problem Solving
Nov 08, 2025
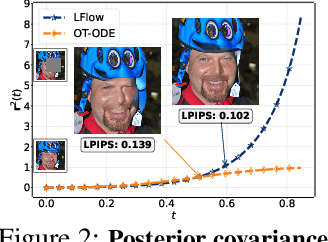

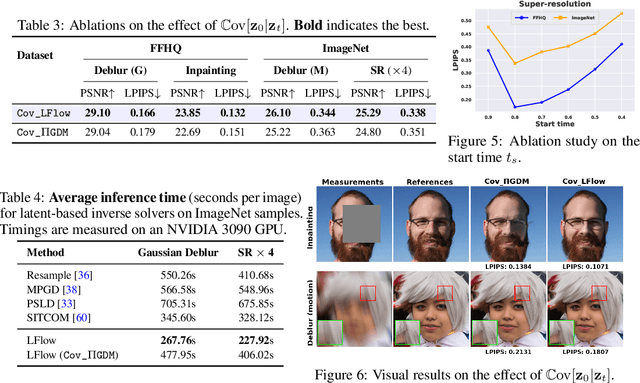
Abstract:Recent advances in inverse problem solving have increasingly adopted flow priors over diffusion models due to their ability to construct straight probability paths from noise to data, thereby enhancing efficiency in both training and inference. However, current flow-based inverse solvers face two primary limitations: (i) they operate directly in pixel space, which demands heavy computational resources for training and restricts scalability to high-resolution images, and (ii) they employ guidance strategies with prior-agnostic posterior covariances, which can weaken alignment with the generative trajectory and degrade posterior coverage. In this paper, we propose LFlow (Latent Refinement via Flows), a training-free framework for solving linear inverse problems via pretrained latent flow priors. LFlow leverages the efficiency of flow matching to perform ODE sampling in latent space along an optimal path. This latent formulation further allows us to introduce a theoretically grounded posterior covariance, derived from the optimal vector field, enabling effective flow guidance. Experimental results demonstrate that our proposed method outperforms state-of-the-art latent diffusion solvers in reconstruction quality across most tasks. The code will be publicly available at https://github.com/hosseinaskari-cs/LFlow .
Importance Sampling for Nonlinear Models
May 18, 2025Abstract:While norm-based and leverage-score-based methods have been extensively studied for identifying "important" data points in linear models, analogous tools for nonlinear models remain significantly underdeveloped. By introducing the concept of the adjoint operator of a nonlinear map, we address this gap and generalize norm-based and leverage-score-based importance sampling to nonlinear settings. We demonstrate that sampling based on these generalized notions of norm and leverage scores provides approximation guarantees for the underlying nonlinear mapping, similar to linear subspace embeddings. As direct applications, these nonlinear scores not only reduce the computational complexity of training nonlinear models by enabling efficient sampling over large datasets but also offer a novel mechanism for model explainability and outlier detection. Our contributions are supported by both theoretical analyses and experimental results across a variety of supervised learning scenarios.
Determinant Estimation under Memory Constraints and Neural Scaling Laws
Mar 06, 2025Abstract:Calculating or accurately estimating log-determinants of large positive semi-definite matrices is of fundamental importance in many machine learning tasks. While its cubic computational complexity can already be prohibitive, in modern applications, even storing the matrices themselves can pose a memory bottleneck. To address this, we derive a novel hierarchical algorithm based on block-wise computation of the LDL decomposition for large-scale log-determinant calculation in memory-constrained settings. In extreme cases where matrices are highly ill-conditioned, accurately computing the full matrix itself may be infeasible. This is particularly relevant when considering kernel matrices at scale, including the empirical Neural Tangent Kernel (NTK) of neural networks trained on large datasets. Under the assumption of neural scaling laws in the test error, we show that the ratio of pseudo-determinants satisfies a power-law relationship, allowing us to derive corresponding scaling laws. This enables accurate estimation of NTK log-determinants from a tiny fraction of the full dataset; in our experiments, this results in a $\sim$100,000$\times$ speedup with improved accuracy over competing approximations. Using these techniques, we successfully estimate log-determinants for dense matrices of extreme sizes, which were previously deemed intractable and inaccessible due to their enormous scale and computational demands.
First-ish Order Methods: Hessian-aware Scalings of Gradient Descent
Feb 06, 2025



Abstract:Gradient descent is the primary workhorse for optimizing large-scale problems in machine learning. However, its performance is highly sensitive to the choice of the learning rate. A key limitation of gradient descent is its lack of natural scaling, which often necessitates expensive line searches or heuristic tuning to determine an appropriate step size. In this paper, we address this limitation by incorporating Hessian information to scale the gradient direction. By accounting for the curvature of the function along the gradient, our adaptive, Hessian-aware scaling method ensures a local unit step size guarantee, even in nonconvex settings. Near a local minimum that satisfies the second-order sufficient conditions, our approach achieves linear convergence with a unit step size. We show that our method converges globally under a significantly weaker version of the standard Lipschitz gradient smoothness assumption. Even when Hessian information is inexact, the local unit step size guarantee and global convergence properties remain valid under mild conditions. Finally, we validate our theoretical results empirically on a range of convex and nonconvex machine learning tasks, showcasing the effectiveness of the approach.
Uncertainty Quantification with the Empirical Neural Tangent Kernel
Feb 05, 2025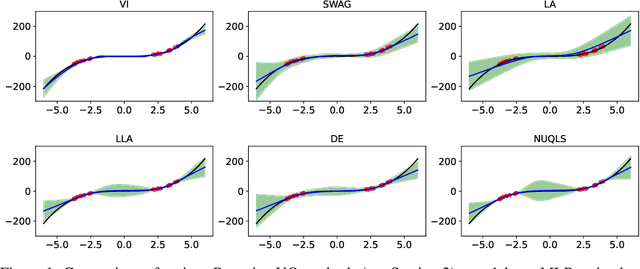
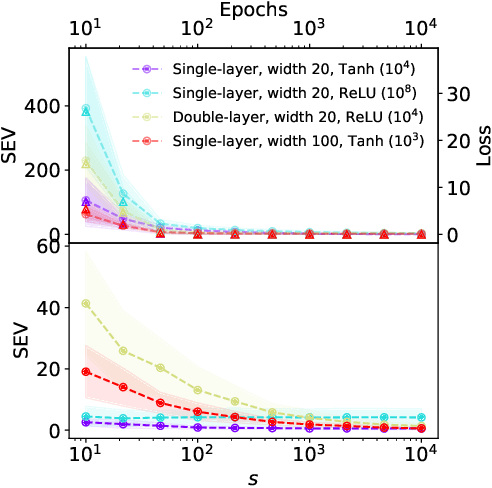
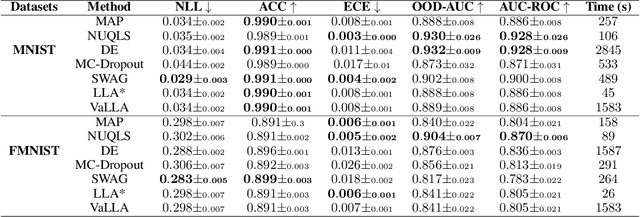
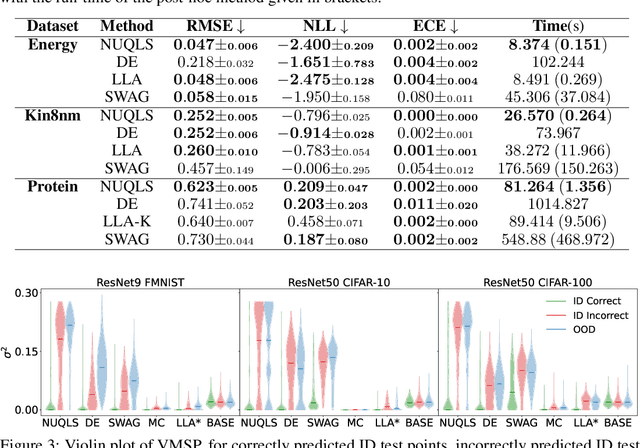
Abstract:While neural networks have demonstrated impressive performance across various tasks, accurately quantifying uncertainty in their predictions is essential to ensure their trustworthiness and enable widespread adoption in critical systems. Several Bayesian uncertainty quantification (UQ) methods exist that are either cheap or reliable, but not both. We propose a post-hoc, sampling-based UQ method for over-parameterized networks at the end of training. Our approach constructs efficient and meaningful deep ensembles by employing a (stochastic) gradient-descent sampling process on appropriately linearized networks. We demonstrate that our method effectively approximates the posterior of a Gaussian process using the empirical Neural Tangent Kernel. Through a series of numerical experiments, we show that our method not only outperforms competing approaches in computational efficiency (often reducing costs by multiple factors) but also maintains state-of-the-art performance across a variety of UQ metrics for both regression and classification tasks.
Manifold Integrated Gradients: Riemannian Geometry for Feature Attribution
May 16, 2024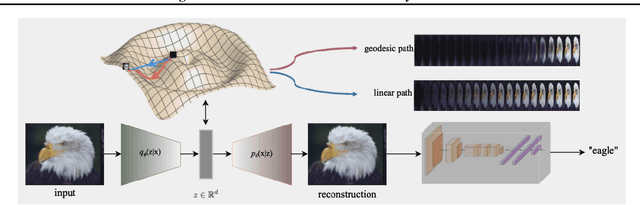
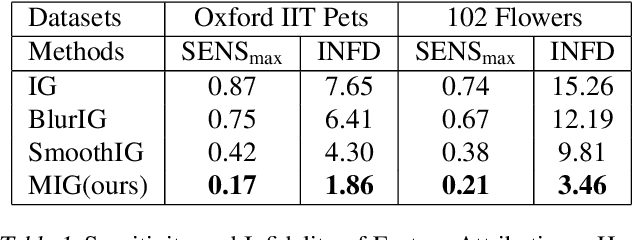
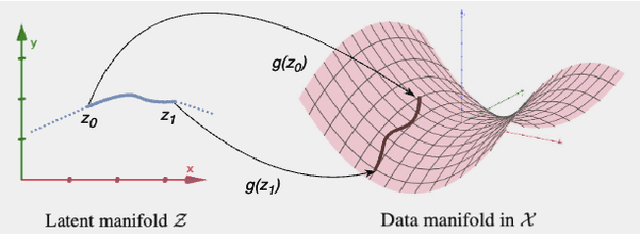
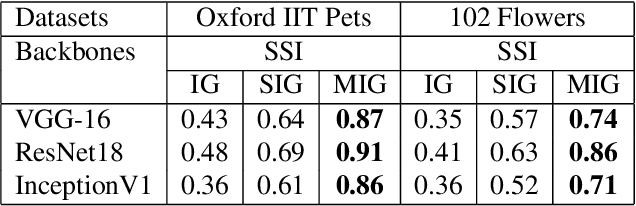
Abstract:In this paper, we dive into the reliability concerns of Integrated Gradients (IG), a prevalent feature attribution method for black-box deep learning models. We particularly address two predominant challenges associated with IG: the generation of noisy feature visualizations for vision models and the vulnerability to adversarial attributional attacks. Our approach involves an adaptation of path-based feature attribution, aligning the path of attribution more closely to the intrinsic geometry of the data manifold. Our experiments utilise deep generative models applied to several real-world image datasets. They demonstrate that IG along the geodesics conforms to the curved geometry of the Riemannian data manifold, generating more perceptually intuitive explanations and, subsequently, substantially increasing robustness to targeted attributional attacks.
Bi-level Guided Diffusion Models for Zero-Shot Medical Imaging Inverse Problems
Apr 04, 2024Abstract:In the realm of medical imaging, inverse problems aim to infer high-quality images from incomplete, noisy measurements, with the objective of minimizing expenses and risks to patients in clinical settings. The Diffusion Models have recently emerged as a promising approach to such practical challenges, proving particularly useful for the zero-shot inference of images from partially acquired measurements in Magnetic Resonance Imaging (MRI) and Computed Tomography (CT). A central challenge in this approach, however, is how to guide an unconditional prediction to conform to the measurement information. Existing methods rely on deficient projection or inefficient posterior score approximation guidance, which often leads to suboptimal performance. In this paper, we propose \underline{\textbf{B}}i-level \underline{G}uided \underline{D}iffusion \underline{M}odels ({BGDM}), a zero-shot imaging framework that efficiently steers the initial unconditional prediction through a \emph{bi-level} guidance strategy. Specifically, BGDM first approximates an \emph{inner-level} conditional posterior mean as an initial measurement-consistent reference point and then solves an \emph{outer-level} proximal optimization objective to reinforce the measurement consistency. Our experimental findings, using publicly available MRI and CT medical datasets, reveal that BGDM is more effective and efficient compared to the baselines, faithfully generating high-fidelity medical images and substantially reducing hallucinatory artifacts in cases of severe degradation.
SALSA: Sequential Approximate Leverage-Score Algorithm with Application in Analyzing Big Time Series Data
Dec 30, 2023Abstract:We develop a new efficient sequential approximate leverage score algorithm, SALSA, using methods from randomized numerical linear algebra (RandNLA) for large matrices. We demonstrate that, with high probability, the accuracy of SALSA's approximations is within $(1 + O({\varepsilon}))$ of the true leverage scores. In addition, we show that the theoretical computational complexity and numerical accuracy of SALSA surpass existing approximations. These theoretical results are subsequently utilized to develop an efficient algorithm, named LSARMA, for fitting an appropriate ARMA model to large-scale time series data. Our proposed algorithm is, with high probability, guaranteed to find the maximum likelihood estimates of the parameters for the true underlying ARMA model. Furthermore, it has a worst-case running time that significantly improves those of the state-of-the-art alternatives in big data regimes. Empirical results on large-scale data strongly support these theoretical results and underscore the efficacy of our new approach.
Non-Uniform Smoothness for Gradient Descent
Nov 15, 2023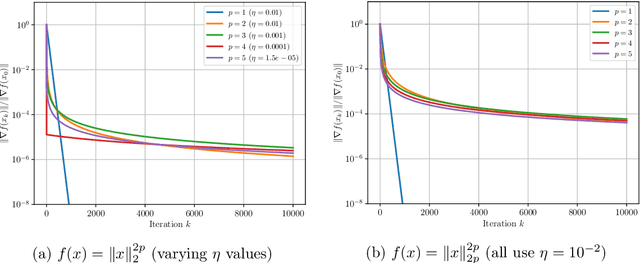
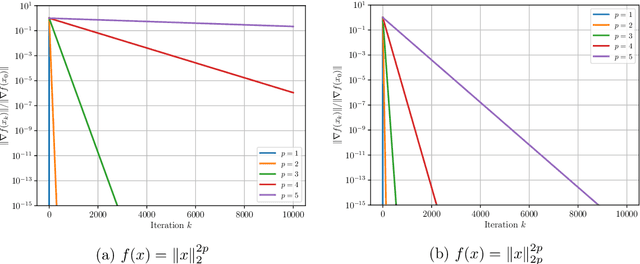
Abstract:The analysis of gradient descent-type methods typically relies on the Lipschitz continuity of the objective gradient. This generally requires an expensive hyperparameter tuning process to appropriately calibrate a stepsize for a given problem. In this work we introduce a local first-order smoothness oracle (LFSO) which generalizes the Lipschitz continuous gradients smoothness condition and is applicable to any twice-differentiable function. We show that this oracle can encode all relevant problem information for tuning stepsizes for a suitably modified gradient descent method and give global and local convergence results. We also show that LFSOs in this modified first-order method can yield global linear convergence rates for non-strongly convex problems with extremely flat minima, and thus improve over the lower bound on rates achievable by general (accelerated) first-order methods.
A PAC-Bayesian Perspective on the Interpolating Information Criterion
Nov 13, 2023Abstract:Deep learning is renowned for its theory-practice gap, whereby principled theory typically fails to provide much beneficial guidance for implementation in practice. This has been highlighted recently by the benign overfitting phenomenon: when neural networks become sufficiently large to interpolate the dataset perfectly, model performance appears to improve with increasing model size, in apparent contradiction with the well-known bias-variance tradeoff. While such phenomena have proven challenging to theoretically study for general models, the recently proposed Interpolating Information Criterion (IIC) provides a valuable theoretical framework to examine performance for overparameterized models. Using the IIC, a PAC-Bayes bound is obtained for a general class of models, characterizing factors which influence generalization performance in the interpolating regime. From the provided bound, we quantify how the test error for overparameterized models achieving effectively zero training error depends on the quality of the implicit regularization imposed by e.g. the combination of model, optimizer, and parameter-initialization scheme; the spectrum of the empirical neural tangent kernel; curvature of the loss landscape; and noise present in the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge