Non-Uniform Smoothness for Gradient Descent
Paper and Code
Nov 15, 2023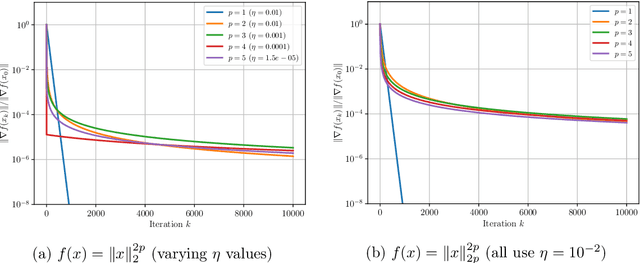
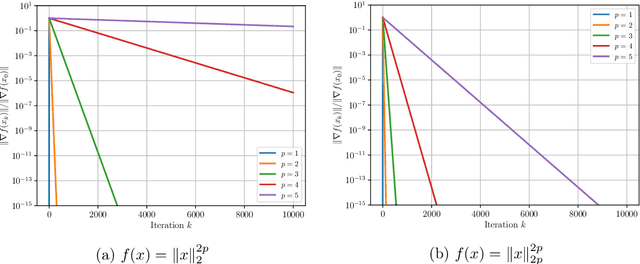
The analysis of gradient descent-type methods typically relies on the Lipschitz continuity of the objective gradient. This generally requires an expensive hyperparameter tuning process to appropriately calibrate a stepsize for a given problem. In this work we introduce a local first-order smoothness oracle (LFSO) which generalizes the Lipschitz continuous gradients smoothness condition and is applicable to any twice-differentiable function. We show that this oracle can encode all relevant problem information for tuning stepsizes for a suitably modified gradient descent method and give global and local convergence results. We also show that LFSOs in this modified first-order method can yield global linear convergence rates for non-strongly convex problems with extremely flat minima, and thus improve over the lower bound on rates achievable by general (accelerated) first-order methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge