Second-order Information Promotes Mini-Batch Robustness in Variance-Reduced Gradients

We show that, for finite-sum minimization problems, incorporating partial second-order information of the objective function can dramatically improve the robustness to mini-batch size of variance-reduced stochastic gradient methods, making them more scalable while retaining their benefits over traditional Newton-type approaches. We demonstrate this phenomenon on a prototypical stochastic second-order algorithm, called Mini-Batch Stochastic Variance-Reduced Newton ($\texttt{Mb-SVRN}$), which combines variance-reduced gradient estimates with access to an approximate Hessian oracle. In particular, we show that when the data size $n$ is sufficiently large, i.e., $n\gg \alpha^2\kappa$, where $\kappa$ is the condition number and $\alpha$ is the Hessian approximation factor, then $\texttt{Mb-SVRN}$ achieves a fast linear convergence rate that is independent of the gradient mini-batch size $b$, as long $b$ is in the range between $1$ and $b_{\max}=O(n/(\alpha \log n))$. Only after increasing the mini-batch size past this critical point $b_{\max}$, the method begins to transition into a standard Newton-type algorithm which is much more sensitive to the Hessian approximation quality. We demonstrate this phenomenon empirically on benchmark optimization tasks showing that, after tuning the step size, the convergence rate of $\texttt{Mb-SVRN}$ remains fast for a wide range of mini-batch sizes, and the dependence of the phase transition point $b_{\max}$ on the Hessian approximation factor $\alpha$ aligns with our theoretical predictions.

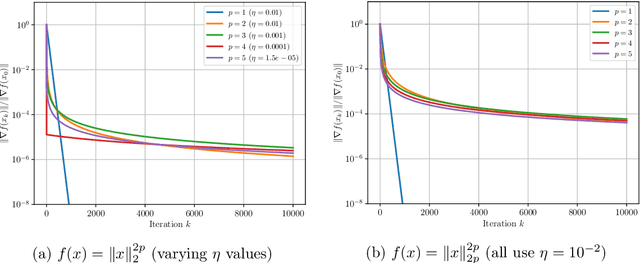
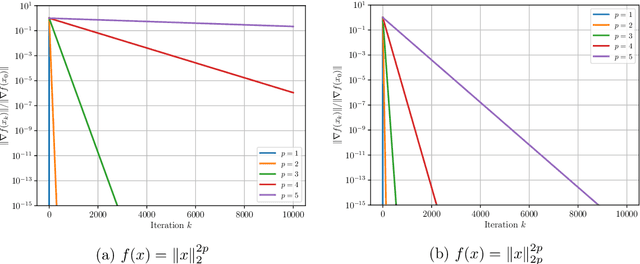
Non-Uniform Smoothness for Gradient Descent

The analysis of gradient descent-type methods typically relies on the Lipschitz continuity of the objective gradient. This generally requires an expensive hyperparameter tuning process to appropriately calibrate a stepsize for a given problem. In this work we introduce a local first-order smoothness oracle (LFSO) which generalizes the Lipschitz continuous gradients smoothness condition and is applicable to any twice-differentiable function. We show that this oracle can encode all relevant problem information for tuning stepsizes for a suitably modified gradient descent method and give global and local convergence results. We also show that LFSOs in this modified first-order method can yield global linear convergence rates for non-strongly convex problems with extremely flat minima, and thus improve over the lower bound on rates achievable by general (accelerated) first-order methods.

Adaptive Consensus: A network pruning approach for decentralized optimization

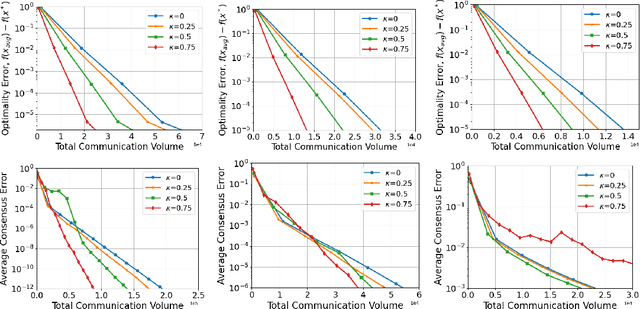
We consider network-based decentralized optimization problems, where each node in the network possesses a local function and the objective is to collectively attain a consensus solution that minimizes the sum of all the local functions. A major challenge in decentralized optimization is the reliance on communication which remains a considerable bottleneck in many applications. To address this challenge, we propose an adaptive randomized communication-efficient algorithmic framework that reduces the volume of communication by periodically tracking the disagreement error and judiciously selecting the most influential and effective edges at each node for communication. Within this framework, we present two algorithms: Adaptive Consensus (AC) to solve the consensus problem and Adaptive Consensus based Gradient Tracking (AC-GT) to solve smooth strongly convex decentralized optimization problems. We establish strong theoretical convergence guarantees for the proposed algorithms and quantify their performance in terms of various algorithmic parameters under standard assumptions. Finally, numerical experiments showcase the effectiveness of the framework in significantly reducing the information exchange required to achieve a consensus solution.

Collaborative and Distributed Bayesian Optimization via Consensus: Showcasing the Power of Collaboration for Optimal Design

Optimal design is a critical yet challenging task within many applications. This challenge arises from the need for extensive trial and error, often done through simulations or running field experiments. Fortunately, sequential optimal design, also referred to as Bayesian optimization when using surrogates with a Bayesian flavor, has played a key role in accelerating the design process through efficient sequential sampling strategies. However, a key opportunity exists nowadays. The increased connectivity of edge devices sets forth a new collaborative paradigm for Bayesian optimization. A paradigm whereby different clients collaboratively borrow strength from each other by effectively distributing their experimentation efforts to improve and fast-track their optimal design process. To this end, we bring the notion of consensus to Bayesian optimization, where clients agree (i.e., reach a consensus) on their next-to-sample designs. Our approach provides a generic and flexible framework that can incorporate different collaboration mechanisms. In lieu of this, we propose transitional collaborative mechanisms where clients initially rely more on each other to maneuver through the early stages with scant data, then, at the late stages, focus on their own objectives to get client-specific solutions. Theoretically, we show the sub-linear growth in regret for our proposed framework. Empirically, through simulated datasets and a real-world collaborative material discovery experiment, we show that our framework can effectively accelerate and improve the optimal design process and benefit all participants.

A Sequential Quadratic Programming Method with High Probability Complexity Bounds for Nonlinear Equality Constrained Stochastic Optimization

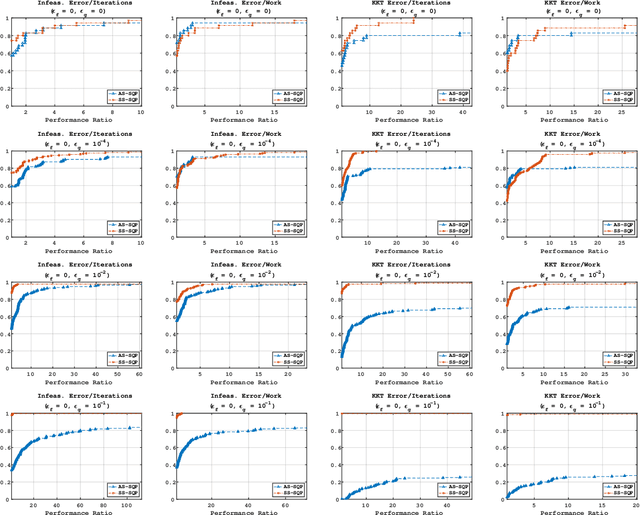
A step-search sequential quadratic programming method is proposed for solving nonlinear equality constrained stochastic optimization problems. It is assumed that constraint function values and derivatives are available, but only stochastic approximations of the objective function and its associated derivatives can be computed via inexact probabilistic zeroth- and first-order oracles. Under reasonable assumptions, a high-probability bound on the iteration complexity of the algorithm to approximate first-order stationarity is derived. Numerical results on standard nonlinear optimization test problems illustrate the advantages and limitations of our proposed method.

A Stochastic Sequential Quadratic Optimization Algorithm for Nonlinear Equality Constrained Optimization with Rank-Deficient Jacobians

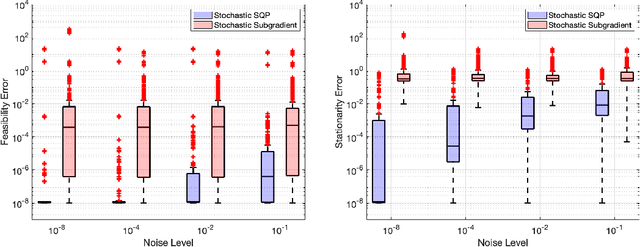
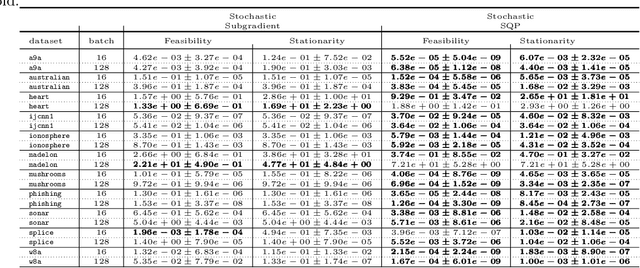
A sequential quadratic optimization algorithm is proposed for solving smooth nonlinear equality constrained optimization problems in which the objective function is defined by an expectation of a stochastic function. The algorithmic structure of the proposed method is based on a step decomposition strategy that is known in the literature to be widely effective in practice, wherein each search direction is computed as the sum of a normal step (toward linearized feasibility) and a tangential step (toward objective decrease in the null space of the constraint Jacobian). However, the proposed method is unique from others in the literature in that it both allows the use of stochastic objective gradient estimates and possesses convergence guarantees even in the setting in which the constraint Jacobians may be rank deficient. The results of numerical experiments demonstrate that the algorithm offers superior performance when compared to popular alternatives.

SONIA: A Symmetric Blockwise Truncated Optimization Algorithm

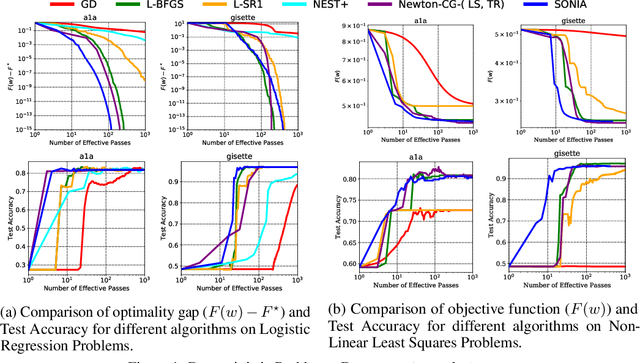
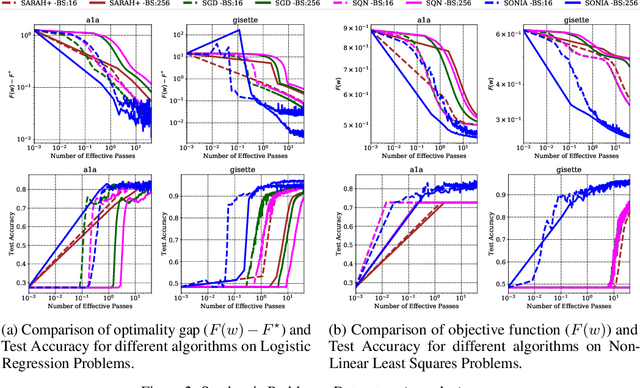
This work presents a new algorithm for empirical risk minimization. The algorithm bridges the gap between first- and second-order methods by computing a search direction that uses a second-order-type update in one subspace, coupled with a scaled steepest descent step in the orthogonal complement. To this end, partial curvature information is incorporated to help with ill-conditioning, while simultaneously allowing the algorithm to scale to the large problem dimensions often encountered in machine learning applications. Theoretical results are presented to confirm that the algorithm converges to a stationary point in both the strongly convex and nonconvex cases. A stochastic variant of the algorithm is also presented, along with corresponding theoretical guarantees. Numerical results confirm the strengths of the new approach on standard machine learning problems.

Finite Difference Neural Networks: Fast Prediction of Partial Differential Equations

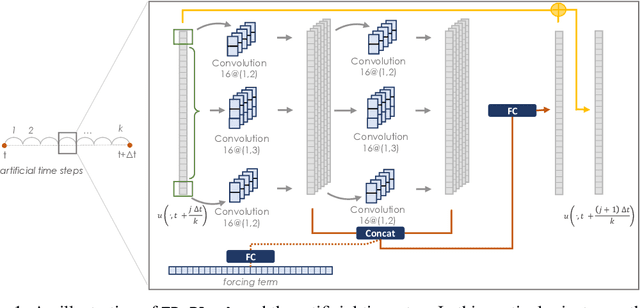
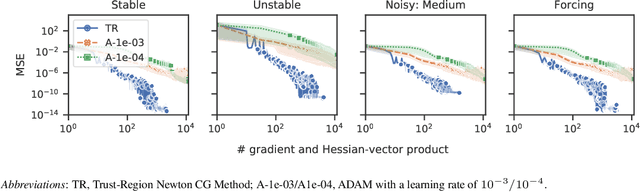
Discovering the underlying behavior of complex systems is an important topic in many science and engineering disciplines. In this paper, we propose a novel neural network framework, finite difference neural networks (FDNet), to learn partial differential equations from data. Specifically, our proposed finite difference inspired network is designed to learn the underlying governing partial differential equations from trajectory data, and to iteratively estimate the future dynamical behavior using only a few trainable parameters. We illustrate the performance (predictive power) of our framework on the heat equation, with and without noise and/or forcing, and compare our results to the Forward Euler method. Moreover, we show the advantages of using a Hessian-Free Trust Region method to train the network.

Scaling Up Quasi-Newton Algorithms: Communication Efficient Distributed SR1

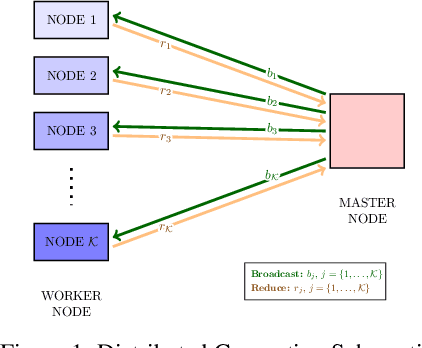
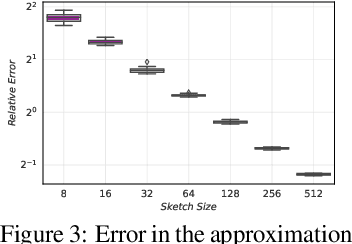
In this paper, we present a scalable distributed implementation of the sampled LSR1 (S-LSR1) algorithm. First, we show that a naive distributed implementation of S-LSR1 requires multiple rounds of expensive communications at every iteration and thus is inefficient. We then propose DS-LSR1, a communication-efficient variant of the S-LSR1 method, that drastically reduces the amount of data communicated at every iteration, that has favorable work-load balancing across nodes and that is matrix-free and inverse-free. The proposed method scales well in terms of both the dimension of the problem and the number of data points. Finally, we illustrate the performance of DS-LSR1 on standard neural network training tasks.

Quasi-Newton Methods for Deep Learning: Forget the Past, Just Sample

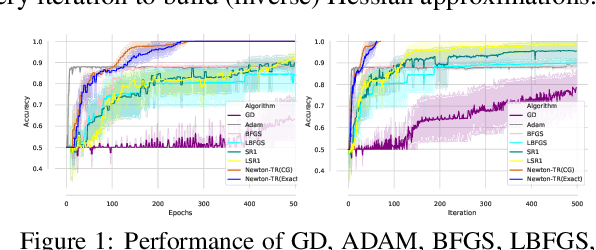
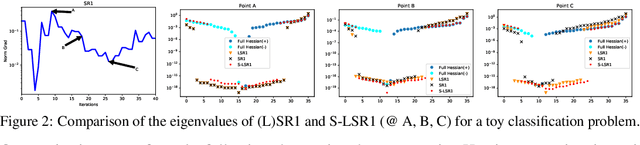
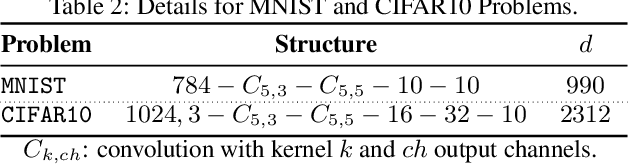
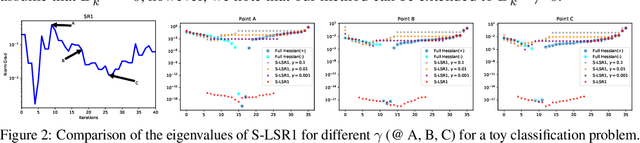
We present two sampled quasi-Newton methods for deep learning: sampled LBFGS (S-LBFGS) and sampled LSR1 (S-LSR1). Contrary to the classical variants of these methods that sequentially build Hessian or inverse Hessian approximations as the optimization progresses, our proposed methods sample points randomly around the current iterate at every iteration to produce these approximations. As a result, the approximations constructed make use of more reliable (recent and local) information, and do not depend on past iterate information that could be significantly stale. Our proposed algorithms are efficient in terms of accessed data points (epochs) and have enough concurrency to take advantage of parallel/distributed computing environments. We provide convergence guarantees for our proposed methods. Numerical tests on a toy classification problem as well as on popular benchmarking neural network training tasks reveal that the methods outperform their classical variants and are competitive with state-of-the-art first-order methods such as ADAM.