Xubo Yue
James
Physics as the Inductive Bias for Causal Discovery
Feb 03, 2026Abstract:Causal discovery is often a data-driven paradigm to analyze complex real-world systems. In parallel, physics-based models such as ordinary differential equations (ODEs) provide mechanistic structure for many dynamical processes. Integrating these paradigms potentially allows physical knowledge to act as an inductive bias, improving identifiability, stability, and robustness of causal discovery in dynamical systems. However, such integration remains challenging: real dynamical systems often exhibit feedback, cyclic interactions, and non-stationary data trend, while many widely used causal discovery methods are formulated under acyclicity or equilibrium-based assumptions. In this work, we propose an integrative causal discovery framework for dynamical systems that leverages partial physical knowledge as an inductive bias. Specifically, we model system evolution as a stochastic differential equation (SDE), where the drift term encodes known ODE dynamics and the diffusion term corresponds to unknown causal couplings beyond the prescribed physics. We develop a scalable sparsity-inducing MLE algorithm that exploits causal graph structure for efficient parameter estimation. Under mild conditions, we establish guarantees to recover the causal graph. Experiments on dynamical systems with diverse causal structures show that our approach improves causal graph recovery and produces more stable, physically consistent estimates than purely data-driven state-of-the-art baselines.
Toward Temporal Causal Representation Learning with Tensor Decomposition
Jul 18, 2025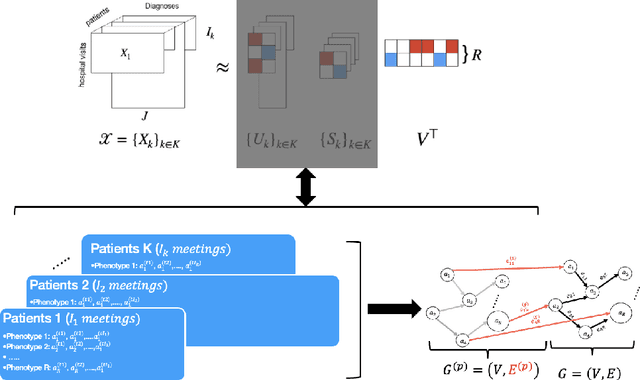
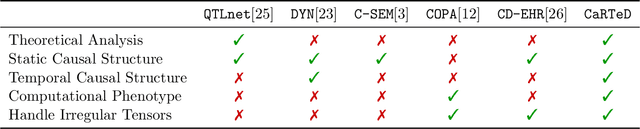
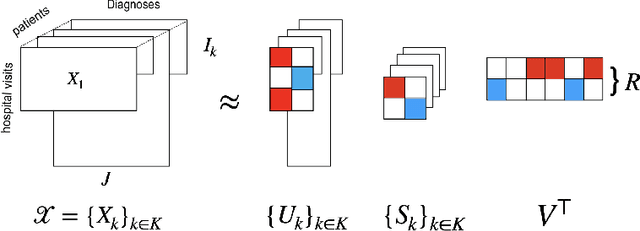
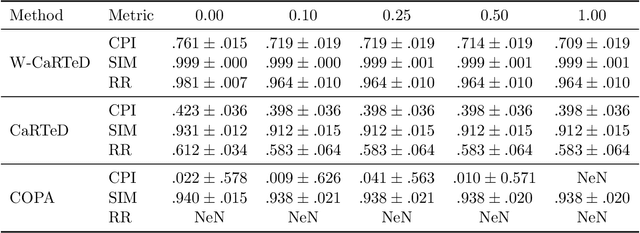
Abstract:Temporal causal representation learning is a powerful tool for uncovering complex patterns in observational studies, which are often represented as low-dimensional time series. However, in many real-world applications, data are high-dimensional with varying input lengths and naturally take the form of irregular tensors. To analyze such data, irregular tensor decomposition is critical for extracting meaningful clusters that capture essential information. In this paper, we focus on modeling causal representation learning based on the transformed information. First, we present a novel causal formulation for a set of latent clusters. We then propose CaRTeD, a joint learning framework that integrates temporal causal representation learning with irregular tensor decomposition. Notably, our framework provides a blueprint for downstream tasks using the learned tensor factors, such as modeling latent structures and extracting causal information, and offers a more flexible regularization design to enhance tensor decomposition. Theoretically, we show that our algorithm converges to a stationary point. More importantly, our results fill the gap in theoretical guarantees for the convergence of state-of-the-art irregular tensor decomposition. Experimental results on synthetic and real-world electronic health record (EHR) datasets (MIMIC-III), with extensive benchmarks from both phenotyping and network recovery perspectives, demonstrate that our proposed method outperforms state-of-the-art techniques and enhances the explainability of causal representations.
Fed-Joint: Joint Modeling of Nonlinear Degradation Signals and Failure Events for Remaining Useful Life Prediction using Federated Learning
Mar 17, 2025
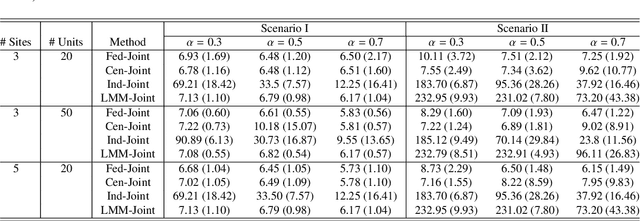


Abstract:Many failure mechanisms of machinery are closely related to the behavior of condition monitoring (CM) signals. To achieve a cost-effective preventive maintenance strategy, accurate remaining useful life (RUL) prediction based on the signals is of paramount importance. However, the CM signals are often recorded at different factories and production lines, with limited amounts of data. Unfortunately, these datasets have rarely been shared between the sites due to data confidentiality and ownership issues, a lack of computing and storage power, and high communication costs associated with data transfer between sites and a data center. Another challenge in real applications is that the CM signals are often not explicitly specified \textit{a priori}, meaning that existing methods, which often usually a parametric form, may not be applicable. To address these challenges, we propose a new prognostic framework for RUL prediction using the joint modeling of nonlinear degradation signals and time-to-failure data within a federated learning scheme. The proposed method constructs a nonparametric degradation model using a federated multi-output Gaussian process and then employs a federated survival model to predict failure times and probabilities for in-service machinery. The superiority of the proposed method over other alternatives is demonstrated through comprehensive simulation studies and a case study using turbofan engine degradation signal data that include run-to-failure events.
Explainable Federated Bayesian Causal Inference and Its Application in Advanced Manufacturing
Jan 10, 2025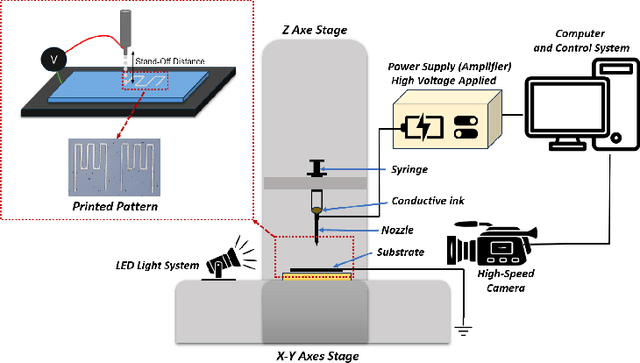
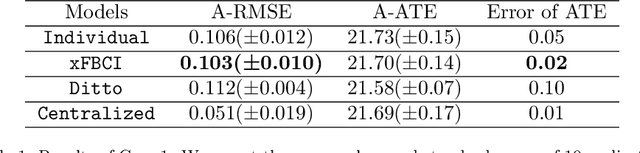
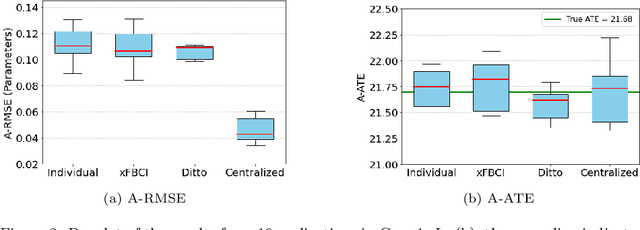
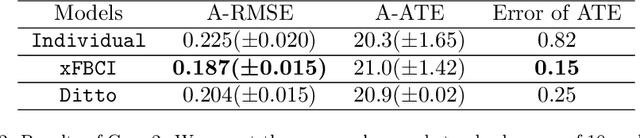
Abstract:Causal inference has recently gained notable attention across various fields like biology, healthcare, and environmental science, especially within explainable artificial intelligence (xAI) systems, for uncovering the causal relationships among multiple variables and outcomes. Yet, it has not been fully recognized and deployed in the manufacturing systems. In this paper, we introduce an explainable, scalable, and flexible federated Bayesian learning framework, \texttt{xFBCI}, designed to explore causality through treatment effect estimation in distributed manufacturing systems. By leveraging federated Bayesian learning, we efficiently estimate posterior of local parameters to derive the propensity score for each client without accessing local private data. These scores are then used to estimate the treatment effect using propensity score matching (PSM). Through simulations on various datasets and a real-world Electrohydrodynamic (EHD) printing data, we demonstrate that our approach outperforms standard Bayesian causal inference methods and several state-of-the-art federated learning benchmarks.
Temporal Causal Discovery in Dynamic Bayesian Networks Using Federated Learning
Dec 13, 2024



Abstract:Traditionally, learning the structure of a Dynamic Bayesian Network has been centralized, with all data pooled in one location. However, in real-world scenarios, data are often dispersed among multiple parties (e.g., companies, devices) that aim to collaboratively learn a Dynamic Bayesian Network while preserving their data privacy and security. In this study, we introduce a federated learning approach for estimating the structure of a Dynamic Bayesian Network from data distributed horizontally across different parties. We propose a distributed structure learning method that leverages continuous optimization so that only model parameters are exchanged during optimization. Experimental results on synthetic and real datasets reveal that our method outperforms other state-of-the-art techniques, particularly when there are many clients with limited individual sample sizes.
Collaborative and Distributed Bayesian Optimization via Consensus: Showcasing the Power of Collaboration for Optimal Design
Jun 25, 2023Abstract:Optimal design is a critical yet challenging task within many applications. This challenge arises from the need for extensive trial and error, often done through simulations or running field experiments. Fortunately, sequential optimal design, also referred to as Bayesian optimization when using surrogates with a Bayesian flavor, has played a key role in accelerating the design process through efficient sequential sampling strategies. However, a key opportunity exists nowadays. The increased connectivity of edge devices sets forth a new collaborative paradigm for Bayesian optimization. A paradigm whereby different clients collaboratively borrow strength from each other by effectively distributing their experimentation efforts to improve and fast-track their optimal design process. To this end, we bring the notion of consensus to Bayesian optimization, where clients agree (i.e., reach a consensus) on their next-to-sample designs. Our approach provides a generic and flexible framework that can incorporate different collaboration mechanisms. In lieu of this, we propose transitional collaborative mechanisms where clients initially rely more on each other to maneuver through the early stages with scant data, then, at the late stages, focus on their own objectives to get client-specific solutions. Theoretically, we show the sub-linear growth in regret for our proposed framework. Empirically, through simulated datasets and a real-world collaborative material discovery experiment, we show that our framework can effectively accelerate and improve the optimal design process and benefit all participants.
Federated Data Analytics: A Study on Linear Models
Jun 15, 2022



Abstract:As edge devices become increasingly powerful, data analytics are gradually moving from a centralized to a decentralized regime where edge compute resources are exploited to process more of the data locally. This regime of analytics is coined as federated data analytics (FDA). In spite of the recent success stories of FDA, most literature focuses exclusively on deep neural networks. In this work, we take a step back to develop an FDA treatment for one of the most fundamental statistical models: linear regression. Our treatment is built upon hierarchical modeling that allows borrowing strength across multiple groups. To this end, we propose two federated hierarchical model structures that provide a shared representation across devices to facilitate information sharing. Notably, our proposed frameworks are capable of providing uncertainty quantification, variable selection, hypothesis testing and fast adaptation to new unseen data. We validate our methods on a range of real-life applications including condition monitoring for aircraft engines. The results show that our FDA treatment for linear models can serve as a competing benchmark model for future development of federated algorithms.
Self-scalable Tanh (Stan): Faster Convergence and Better Generalization in Physics-informed Neural Networks
Apr 29, 2022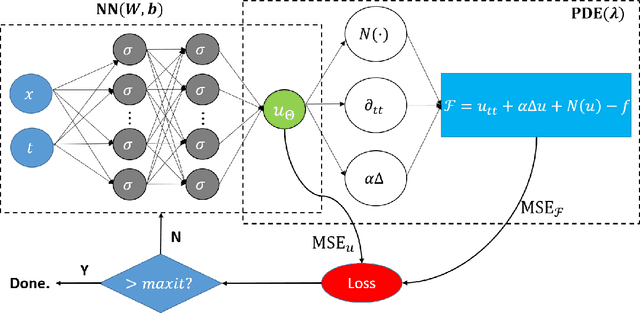
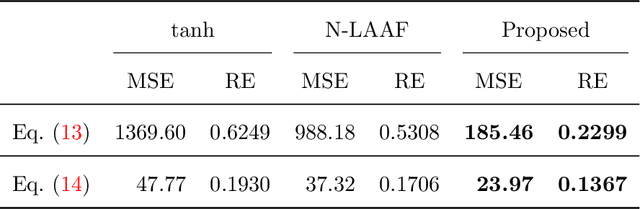
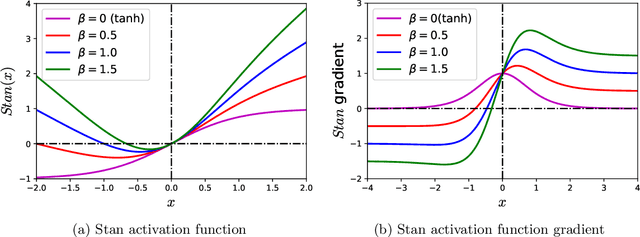
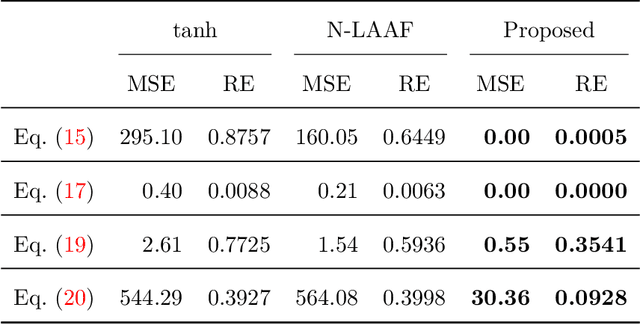
Abstract:Physics-informed Neural Networks (PINNs) are gaining attention in the engineering and scientific literature for solving a range of differential equations with applications in weather modeling, healthcare, manufacturing, etc. Poor scalability is one of the barriers to utilizing PINNs for many real-world problems. To address this, a Self-scalable tanh (Stan) activation function is proposed for the PINNs. The proposed Stan function is smooth, non-saturating, and has a trainable parameter. During training, it can allow easy flow of gradients to compute the required derivatives and also enable systematic scaling of the input-output mapping. It is shown theoretically that the PINNs with the proposed Stan function have no spurious stationary points when using gradient descent algorithms. The proposed Stan is tested on a number of numerical studies involving general regression problems. It is subsequently used for solving multiple forward problems, which involve second-order derivatives and multiple dimensions, and an inverse problem where the thermal diffusivity of a rod is predicted with heat conduction data. These case studies establish empirically that the Stan activation function can achieve better training and more accurate predictions than the existing activation functions in the literature.
Federated Gaussian Process: Convergence, Automatic Personalization and Multi-fidelity Modeling
Nov 28, 2021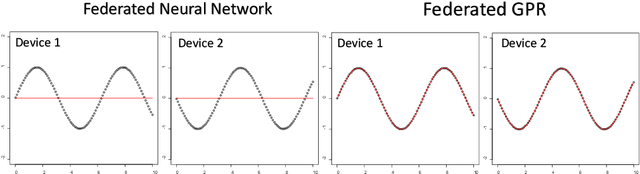

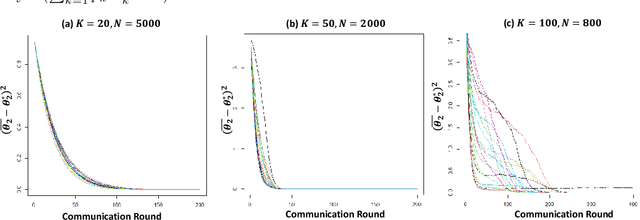
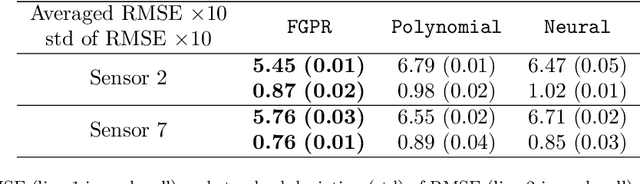
Abstract:In this paper, we propose \texttt{FGPR}: a Federated Gaussian process ($\mathcal{GP}$) regression framework that uses an averaging strategy for model aggregation and stochastic gradient descent for local client computations. Notably, the resulting global model excels in personalization as \texttt{FGPR} jointly learns a global $\mathcal{GP}$ prior across all clients. The predictive posterior then is obtained by exploiting this prior and conditioning on local data which encodes personalized features from a specific client. Theoretically, we show that \texttt{FGPR} converges to a critical point of the full log-likelihood function, subject to statistical error. Through extensive case studies we show that \texttt{FGPR} excels in a wide range of applications and is a promising approach for privacy-preserving multi-fidelity data modeling.
The Internet of Federated Things : A Vision for the Future and In-depth Survey of Data-driven Approaches for Federated Learning
Nov 09, 2021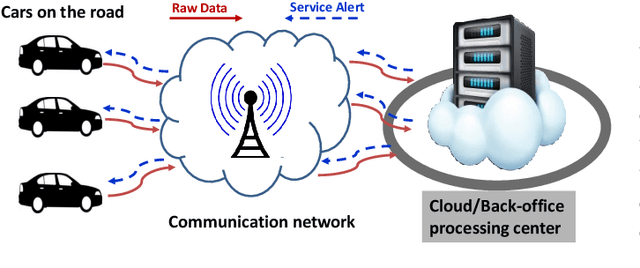
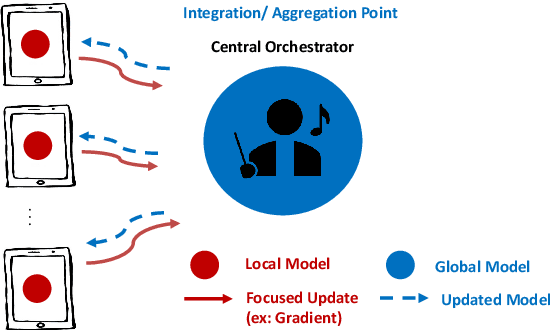
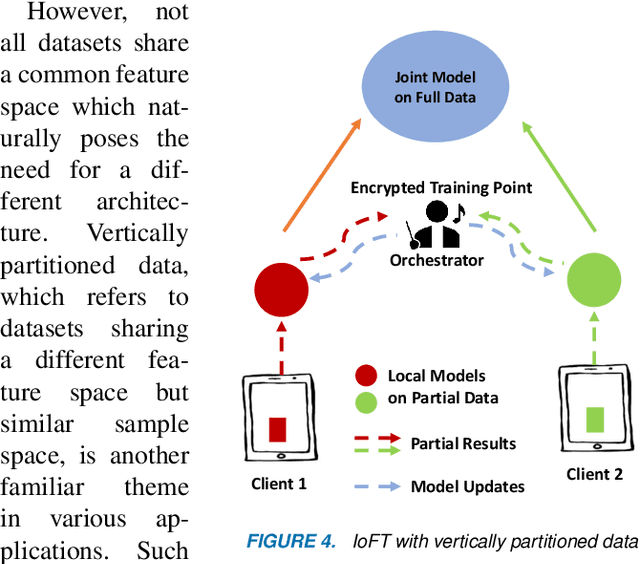
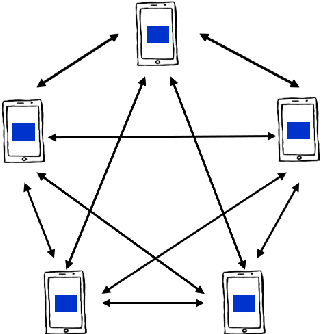
Abstract:The Internet of Things (IoT) is on the verge of a major paradigm shift. In the IoT system of the future, IoFT, the cloud will be substituted by the crowd where model training is brought to the edge, allowing IoT devices to collaboratively extract knowledge and build smart analytics/models while keeping their personal data stored locally. This paradigm shift was set into motion by the tremendous increase in computational power on IoT devices and the recent advances in decentralized and privacy-preserving model training, coined as federated learning (FL). This article provides a vision for IoFT and a systematic overview of current efforts towards realizing this vision. Specifically, we first introduce the defining characteristics of IoFT and discuss FL data-driven approaches, opportunities, and challenges that allow decentralized inference within three dimensions: (i) a global model that maximizes utility across all IoT devices, (ii) a personalized model that borrows strengths across all devices yet retains its own model, (iii) a meta-learning model that quickly adapts to new devices or learning tasks. We end by describing the vision and challenges of IoFT in reshaping different industries through the lens of domain experts. Those industries include manufacturing, transportation, energy, healthcare, quality & reliability, business, and computing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge