Neural Operator for Accelerating Coronal Magnetic Field Model

Studying the sun's outer atmosphere is challenging due to its complex magnetic fields impacting solar activities. Magnetohydrodynamics (MHD) simulations help model these interactions but are extremely time-consuming (usually on a scale of days). Our research applies the Fourier Neural Operator (FNO) to accelerate the coronal magnetic field modeling, specifically, the Bifrost MHD model. We apply Tensorized FNO (TFNO) to generate solutions from partial differential equations (PDEs) over a 3D domain efficiently. TFNO's performance is compared with other deep learning methods, highlighting its accuracy and scalability. Physics analysis confirms that TFNO is reliable and capable of accelerating MHD simulations with high precision. This advancement improves efficiency in data handling, enhances predictive capabilities, and provides a better understanding of magnetic topologies.

Self-scalable Tanh (Stan): Faster Convergence and Better Generalization in Physics-informed Neural Networks

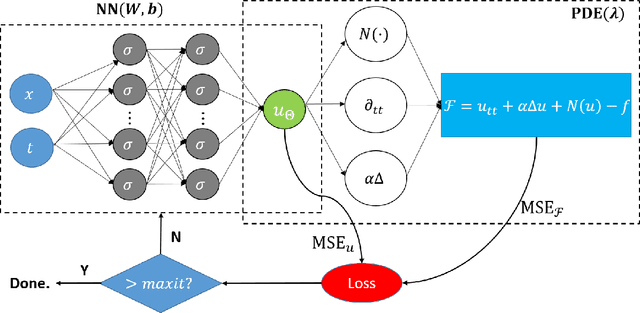
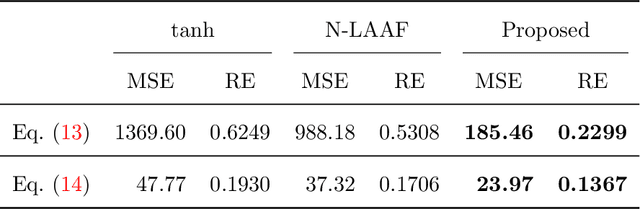
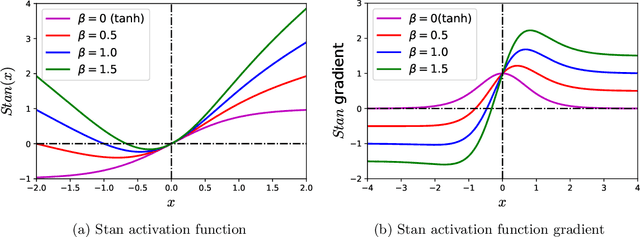
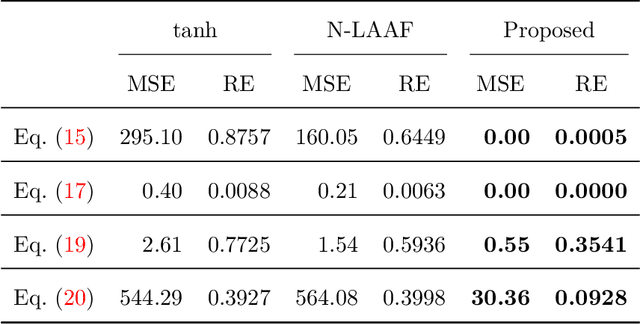
Physics-informed Neural Networks (PINNs) are gaining attention in the engineering and scientific literature for solving a range of differential equations with applications in weather modeling, healthcare, manufacturing, etc. Poor scalability is one of the barriers to utilizing PINNs for many real-world problems. To address this, a Self-scalable tanh (Stan) activation function is proposed for the PINNs. The proposed Stan function is smooth, non-saturating, and has a trainable parameter. During training, it can allow easy flow of gradients to compute the required derivatives and also enable systematic scaling of the input-output mapping. It is shown theoretically that the PINNs with the proposed Stan function have no spurious stationary points when using gradient descent algorithms. The proposed Stan is tested on a number of numerical studies involving general regression problems. It is subsequently used for solving multiple forward problems, which involve second-order derivatives and multiple dimensions, and an inverse problem where the thermal diffusivity of a rod is predicted with heat conduction data. These case studies establish empirically that the Stan activation function can achieve better training and more accurate predictions than the existing activation functions in the literature.