Federated Gaussian Process: Convergence, Automatic Personalization and Multi-fidelity Modeling
Paper and Code
Nov 28, 2021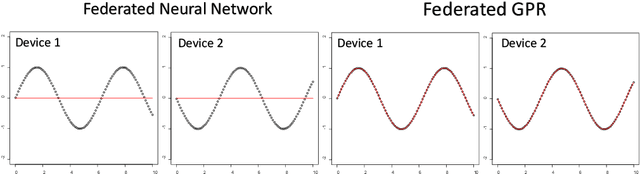

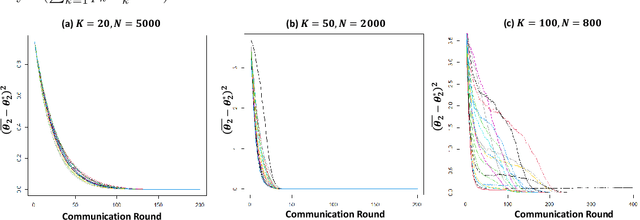
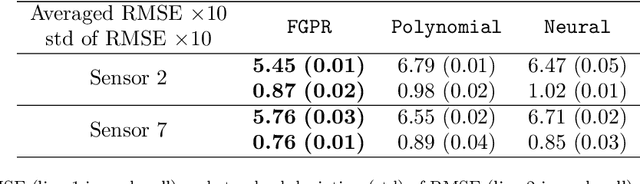
In this paper, we propose \texttt{FGPR}: a Federated Gaussian process ($\mathcal{GP}$) regression framework that uses an averaging strategy for model aggregation and stochastic gradient descent for local client computations. Notably, the resulting global model excels in personalization as \texttt{FGPR} jointly learns a global $\mathcal{GP}$ prior across all clients. The predictive posterior then is obtained by exploiting this prior and conditioning on local data which encodes personalized features from a specific client. Theoretically, we show that \texttt{FGPR} converges to a critical point of the full log-likelihood function, subject to statistical error. Through extensive case studies we show that \texttt{FGPR} excels in a wide range of applications and is a promising approach for privacy-preserving multi-fidelity data modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge