Toward Temporal Causal Representation Learning with Tensor Decomposition

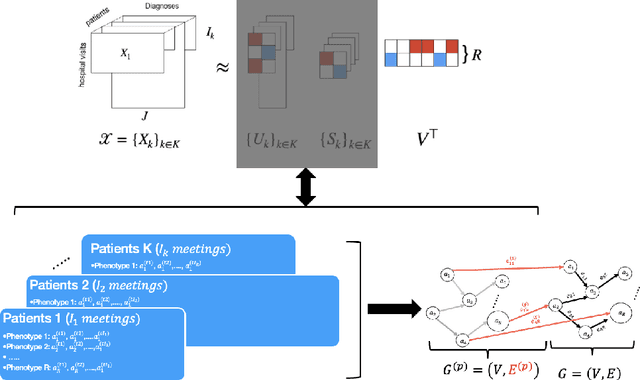
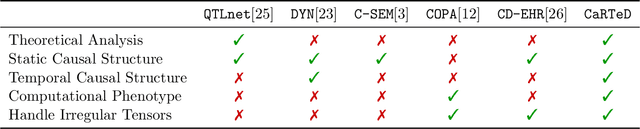
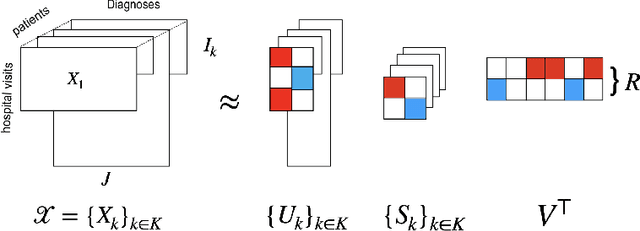
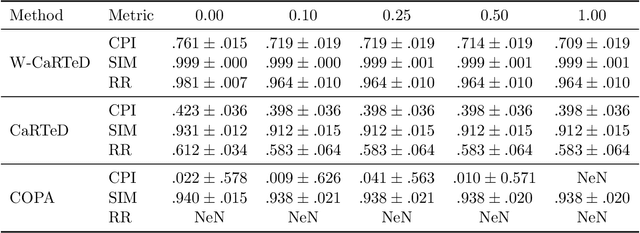
Temporal causal representation learning is a powerful tool for uncovering complex patterns in observational studies, which are often represented as low-dimensional time series. However, in many real-world applications, data are high-dimensional with varying input lengths and naturally take the form of irregular tensors. To analyze such data, irregular tensor decomposition is critical for extracting meaningful clusters that capture essential information. In this paper, we focus on modeling causal representation learning based on the transformed information. First, we present a novel causal formulation for a set of latent clusters. We then propose CaRTeD, a joint learning framework that integrates temporal causal representation learning with irregular tensor decomposition. Notably, our framework provides a blueprint for downstream tasks using the learned tensor factors, such as modeling latent structures and extracting causal information, and offers a more flexible regularization design to enhance tensor decomposition. Theoretically, we show that our algorithm converges to a stationary point. More importantly, our results fill the gap in theoretical guarantees for the convergence of state-of-the-art irregular tensor decomposition. Experimental results on synthetic and real-world electronic health record (EHR) datasets (MIMIC-III), with extensive benchmarks from both phenotyping and network recovery perspectives, demonstrate that our proposed method outperforms state-of-the-art techniques and enhances the explainability of causal representations.

EFiGP: Eigen-Fourier Physics-Informed Gaussian Process for Inference of Dynamic Systems

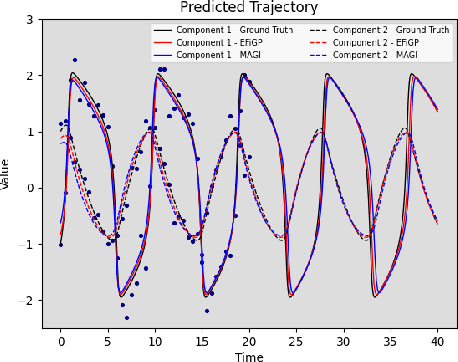
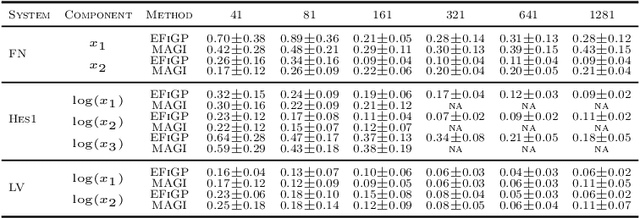
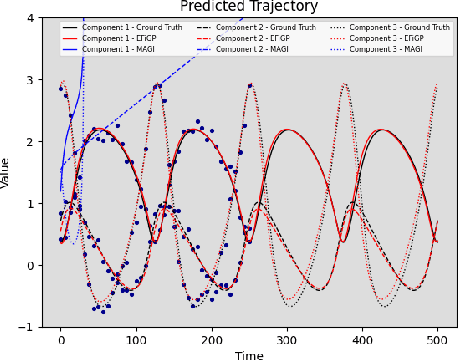
Parameter estimation and trajectory reconstruction for data-driven dynamical systems governed by ordinary differential equations (ODEs) are essential tasks in fields such as biology, engineering, and physics. These inverse problems -- estimating ODE parameters from observational data -- are particularly challenging when the data are noisy, sparse, and the dynamics are nonlinear. We propose the Eigen-Fourier Physics-Informed Gaussian Process (EFiGP), an algorithm that integrates Fourier transformation and eigen-decomposition into a physics-informed Gaussian Process framework. This approach eliminates the need for numerical integration, significantly enhancing computational efficiency and accuracy. Built on a principled Bayesian framework, EFiGP incorporates the ODE system through probabilistic conditioning, enforcing governing equations in the Fourier domain while truncating high-frequency terms to achieve denoising and computational savings. The use of eigen-decomposition further simplifies Gaussian Process covariance operations, enabling efficient recovery of trajectories and parameters even in dense-grid settings. We validate the practical effectiveness of EFiGP on three benchmark examples, demonstrating its potential for reliable and interpretable modeling of complex dynamical systems while addressing key challenges in trajectory recovery and computational cost.

Temporal Causal Discovery in Dynamic Bayesian Networks Using Federated Learning

Traditionally, learning the structure of a Dynamic Bayesian Network has been centralized, with all data pooled in one location. However, in real-world scenarios, data are often dispersed among multiple parties (e.g., companies, devices) that aim to collaboratively learn a Dynamic Bayesian Network while preserving their data privacy and security. In this study, we introduce a federated learning approach for estimating the structure of a Dynamic Bayesian Network from data distributed horizontally across different parties. We propose a distributed structure learning method that leverages continuous optimization so that only model parameters are exchanged during optimization. Experimental results on synthetic and real datasets reveal that our method outperforms other state-of-the-art techniques, particularly when there are many clients with limited individual sample sizes.

Training Sparse Neural Networks using Compressed Sensing

Pruning the weights of neural networks is an effective and widely-used technique for reducing model size and inference complexity. We develop and test a novel method based on compressed sensing which combines the pruning and training into a single step. Specifically, we utilize an adaptively weighted $\ell^1$ penalty on the weights during training, which we combine with a generalization of the regularized dual averaging (RDA) algorithm in order to train sparse neural networks. The adaptive weighting we introduce corresponds to a novel regularizer based on the logarithm of the absolute value of the weights. Numerical experiments on the CIFAR-10 and CIFAR-100 datasets demonstrate that our method 1) trains sparser, more accurate networks than existing state-of-the-art methods; 2) can also be used effectively to obtain structured sparsity; 3) can be used to train sparse networks from scratch, i.e. from a random initialization, as opposed to initializing with a well-trained base model; 4) acts as an effective regularizer, improving generalization accuracy.

A machine learning method correlating pulse pressure wave data with pregnancy

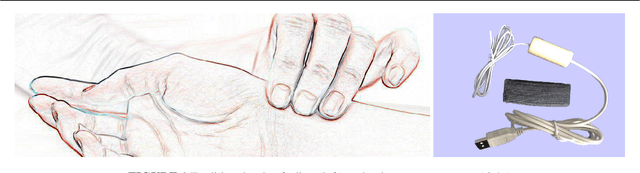
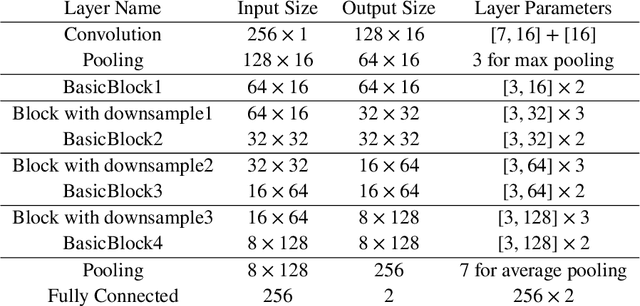
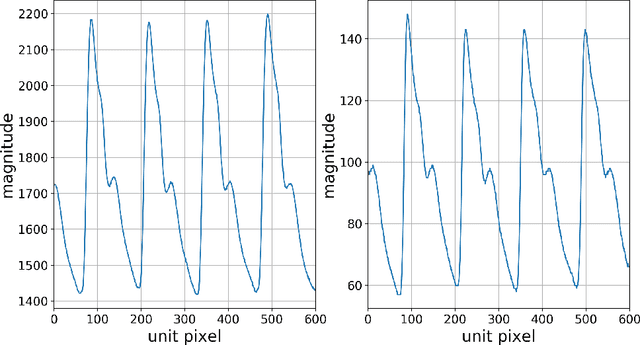
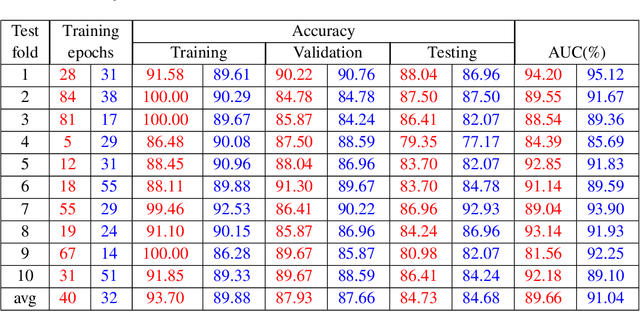
Pulse feeling, representing the tactile arterial palpation of the heartbeat, has been widely used in traditional Chinese medicine (TCM) to diagnose various diseases. The quantitative relationship between the pulse wave and health conditions however has not been investigated in modern medicine. In this paper, we explored the correlation between pulse pressure wave (PPW), rather than the pulse key features in TCM, and pregnancy by using deep learning technology. This computational approach shows that the accuracy of pregnancy detection by the PPW is 84% with an AUC of 91%. Our study is a proof of concept of pulse diagnosis and will also motivate further sophisticated investigations on pulse waves.