Linear Transformers as VAR Models: Aligning Autoregressive Attention Mechanisms with Autoregressive Forecasting

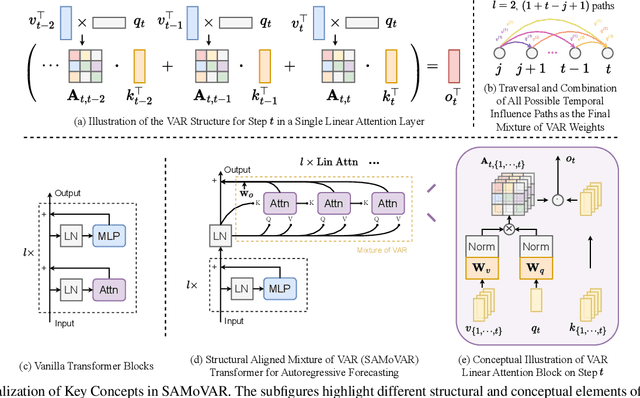
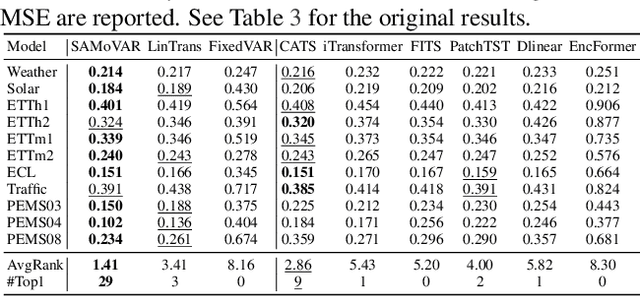
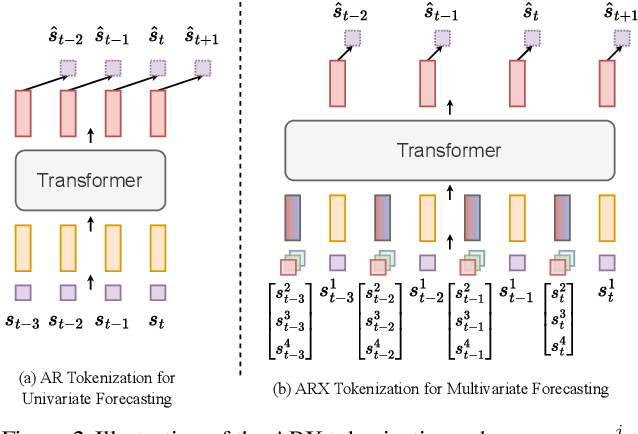
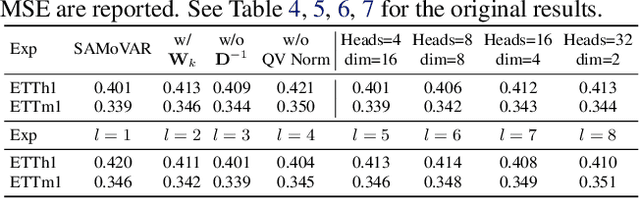
Autoregressive attention-based time series forecasting (TSF) has drawn increasing interest, with mechanisms like linear attention sometimes outperforming vanilla attention. However, deeper Transformer architectures frequently misalign with autoregressive objectives, obscuring the underlying VAR structure embedded within linear attention and hindering their ability to capture the data generative processes in TSF. In this work, we first show that a single linear attention layer can be interpreted as a dynamic vector autoregressive (VAR) structure. We then explain that existing multi-layer Transformers have structural mismatches with the autoregressive forecasting objective, which impair interpretability and generalization ability. To address this, we show that by rearranging the MLP, attention, and input-output flow, multi-layer linear attention can also be aligned as a VAR model. Then, we propose Structural Aligned Mixture of VAR (SAMoVAR), a linear Transformer variant that integrates interpretable dynamic VAR weights for multivariate TSF. By aligning the Transformer architecture with autoregressive objectives, SAMoVAR delivers improved performance, interpretability, and computational efficiency, comparing to SOTA TSF models.

EFiGP: Eigen-Fourier Physics-Informed Gaussian Process for Inference of Dynamic Systems

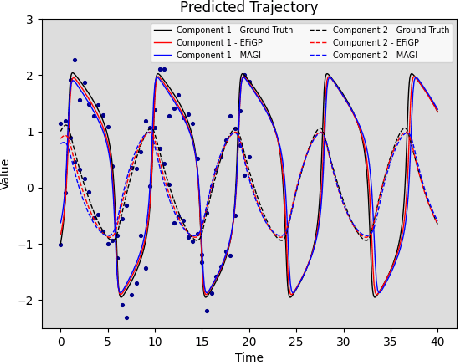
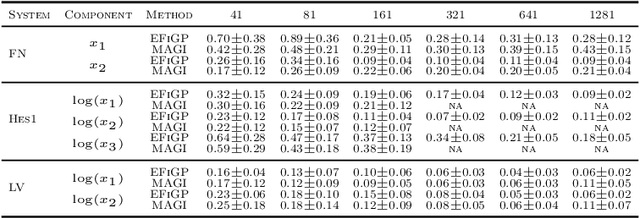
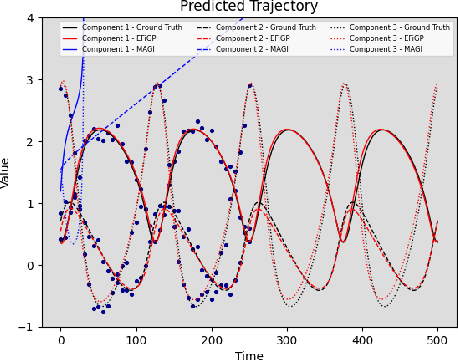
Parameter estimation and trajectory reconstruction for data-driven dynamical systems governed by ordinary differential equations (ODEs) are essential tasks in fields such as biology, engineering, and physics. These inverse problems -- estimating ODE parameters from observational data -- are particularly challenging when the data are noisy, sparse, and the dynamics are nonlinear. We propose the Eigen-Fourier Physics-Informed Gaussian Process (EFiGP), an algorithm that integrates Fourier transformation and eigen-decomposition into a physics-informed Gaussian Process framework. This approach eliminates the need for numerical integration, significantly enhancing computational efficiency and accuracy. Built on a principled Bayesian framework, EFiGP incorporates the ODE system through probabilistic conditioning, enforcing governing equations in the Fourier domain while truncating high-frequency terms to achieve denoising and computational savings. The use of eigen-decomposition further simplifies Gaussian Process covariance operations, enabling efficient recovery of trajectories and parameters even in dense-grid settings. We validate the practical effectiveness of EFiGP on three benchmark examples, demonstrating its potential for reliable and interpretable modeling of complex dynamical systems while addressing key challenges in trajectory recovery and computational cost.

Coupled Integral PINN for conservation law

The Physics-Informed Neural Network (PINN) is an innovative approach to solve a diverse array of partial differential equations (PDEs) leveraging the power of neural networks. This is achieved by minimizing the residual loss associated with the explicit physical information, usually coupled with data derived from initial and boundary conditions. However, a challenge arises in the context of nonlinear conservation laws where derivatives are undefined at shocks, leading to solutions that deviate from the true physical phenomena. To solve this issue, the physical solution must be extracted from the weak formulation of the PDE and is typically further bounded by entropy conditions. Within the numerical framework, finite volume methods (FVM) are employed to address conservation laws. These methods resolve the integral form of conservation laws and delineate the shock characteristics. Inspired by the principles underlying FVM, this paper introduces a novel Coupled Integrated PINN methodology that involves fitting the integral solutions of equations using additional neural networks. This technique not only augments the conventional PINN's capability in modeling shock waves, but also eliminates the need for spatial and temporal discretization. As such, it bypasses the complexities of numerical integration and reconstruction associated with non-convex fluxes. Finally, we show that the proposed new Integrated PINN performs well in conservative law and outperforms the vanilla PINN when tackle the challenging shock problems using examples of Burger's equation, Buckley-Leverett Equation and Euler System.

Autoregressive Moving-average Attention Mechanism for Time Series Forecasting

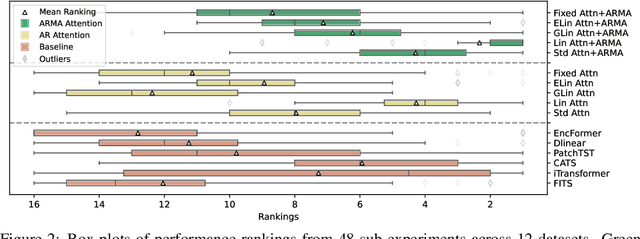
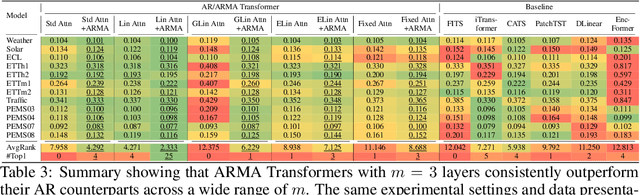
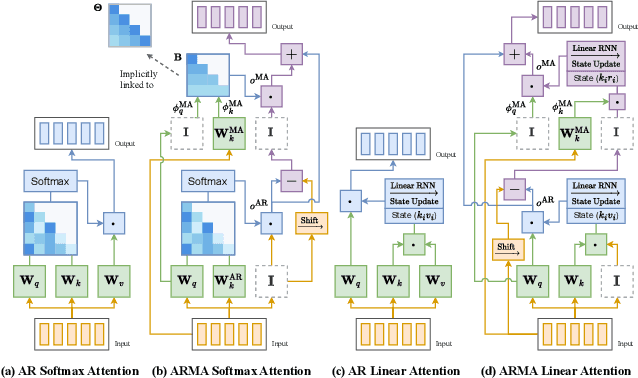
We propose an Autoregressive (AR) Moving-average (MA) attention structure that can adapt to various linear attention mechanisms, enhancing their ability to capture long-range and local temporal patterns in time series. In this paper, we first demonstrate that, for the time series forecasting (TSF) task, the previously overlooked decoder-only autoregressive Transformer model can achieve results comparable to the best baselines when appropriate tokenization and training methods are applied. Moreover, inspired by the ARMA model from statistics and recent advances in linear attention, we introduce the full ARMA structure into existing autoregressive attention mechanisms. By using an indirect MA weight generation method, we incorporate the MA term while maintaining the time complexity and parameter size of the underlying efficient attention models. We further explore how indirect parameter generation can produce implicit MA weights that align with the modeling requirements for local temporal impacts. Experimental results show that incorporating the ARMA structure consistently improves the performance of various AR attentions on TSF tasks, achieving state-of-the-art results.

Inverse Probability of Treatment Weighting with Deep Sequence Models Enables Accurate treatment effect Estimation from Electronic Health Records

Observational data have been actively used to estimate treatment effect, driven by the growing availability of electronic health records (EHRs). However, EHRs typically consist of longitudinal records, often introducing time-dependent confoundings that hinder the unbiased estimation of treatment effect. Inverse probability of treatment weighting (IPTW) is a widely used propensity score method since it provides unbiased treatment effect estimation and its derivation is straightforward. In this study, we aim to utilize IPTW to estimate treatment effect in the presence of time-dependent confounding using claims records. Previous studies have utilized propensity score methods with features derived from claims records through feature processing, which generally requires domain knowledge and additional resources to extract information to accurately estimate propensity scores. Deep sequence models, particularly recurrent neural networks and self-attention-based architectures, have demonstrated good performance in modeling EHRs for various downstream tasks. We propose that these deep sequence models can provide accurate IPTW estimation of treatment effect by directly estimating the propensity scores from claims records without the need for feature processing. We empirically demonstrate this by conducting comprehensive evaluations using synthetic and semi-synthetic datasets.

In-context Time Series Predictor

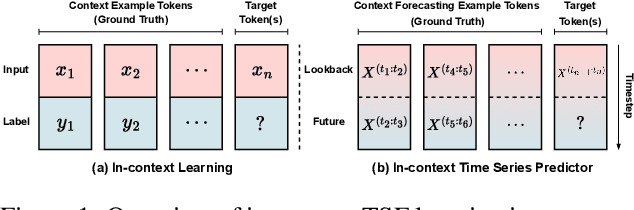
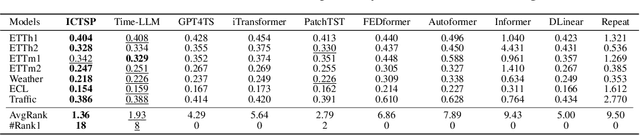
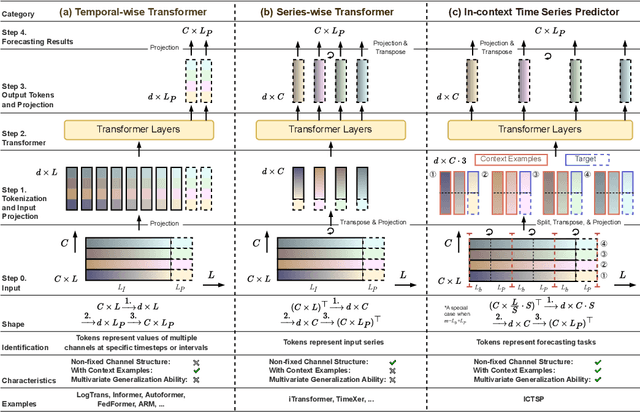
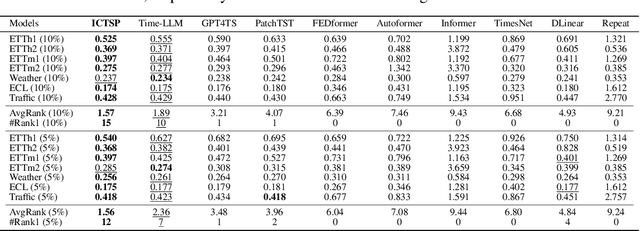
Recent Transformer-based large language models (LLMs) demonstrate in-context learning ability to perform various functions based solely on the provided context, without updating model parameters. To fully utilize the in-context capabilities in time series forecasting (TSF) problems, unlike previous Transformer-based or LLM-based time series forecasting methods, we reformulate "time series forecasting tasks" as input tokens by constructing a series of (lookback, future) pairs within the tokens. This method aligns more closely with the inherent in-context mechanisms, and is more parameter-efficient without the need of using pre-trained LLM parameters. Furthermore, it addresses issues such as overfitting in existing Transformer-based TSF models, consistently achieving better performance across full-data, few-shot, and zero-shot settings compared to previous architectures.

Identification of Craving Maps among Marijuana Users via Analysis of Functional Brain Networks with High-Order Attention Graph Neural Networks

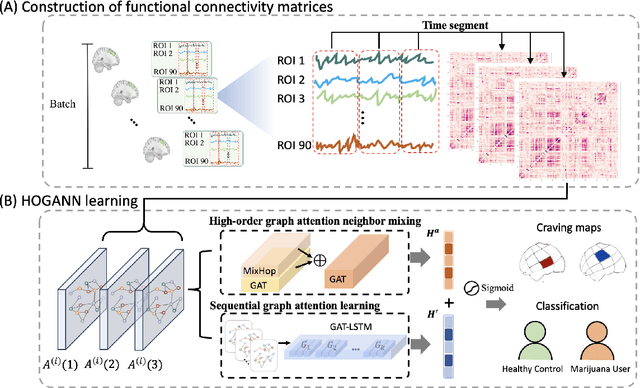
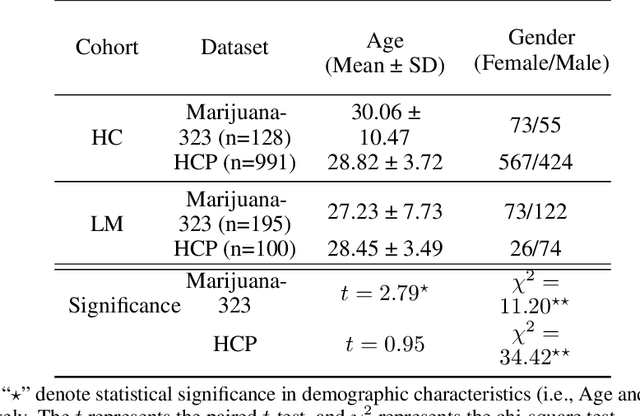
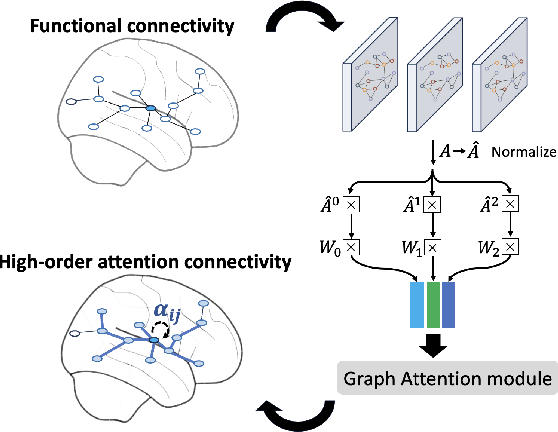
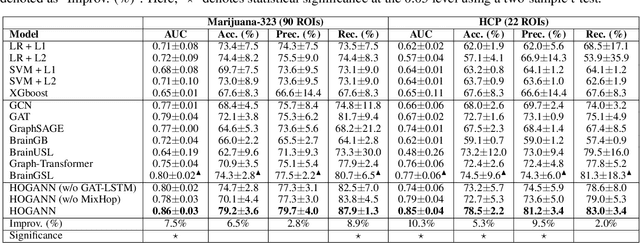
The consumption of high doses of marijuana can have significant psychological and social impacts. In this study, we propose an interpretable novel framework called the HOGAB (High-Order Graph Attention Neural Networks) model for addictive Marijuana classification and analysis of the localized network clusters that demonstrated abnormal brain activities among chronic marijuana users. The HOGAB integrates dynamic intrinsic functional networks with LSTM technology to capture temporal patterns in fMRI time series of marijuana users. We employed the high-order attention module in neighborhood nodes for information fusion and message passing, enhancing community clustering analysis for long-term marijuana users. Furthermore, we improve the overall classification ability of the model by incorporating attention mechanisms, achieving an AUC of 85.1% and an accuracy of 80.7% in classification, higher than the comparison algoirthms. Specifically, we identified the most relevant subnetworks and cognitive regions that are influenced by persistent marijuana usage, revealing that chronic marijuana consumption adversely affects cognitive control, particularly within the Dorsal Attention and Frontoparietal networks, which are essential for attentional, cognitive and higher cognitive functions. The results show that our proposed model is capable of accurately predicting craving bahavior and identifying brain maps associated with long-term cravings, and thus pinpointing brain regions that are important for analysis.

CATS: Enhancing Multivariate Time Series Forecasting by Constructing Auxiliary Time Series as Exogenous Variables

For Multivariate Time Series Forecasting (MTSF), recent deep learning applications show that univariate models frequently outperform multivariate ones. To address the difficiency in multivariate models, we introduce a method to Construct Auxiliary Time Series (CATS) that functions like a 2D temporal-contextual attention mechanism, which generates Auxiliary Time Series (ATS) from Original Time Series (OTS) to effectively represent and incorporate inter-series relationships for forecasting. Key principles of ATS - continuity, sparsity, and variability - are identified and implemented through different modules. Even with a basic 2-layer MLP as core predictor, CATS achieves state-of-the-art, significantly reducing complexity and parameters compared to previous multivariate models, marking it an efficient and transferable MTSF solution.

ARM: Refining Multivariate Forecasting with Adaptive Temporal-Contextual Learning

Long-term time series forecasting (LTSF) is important for various domains but is confronted by challenges in handling the complex temporal-contextual relationships. As multivariate input models underperforming some recent univariate counterparts, we posit that the issue lies in the inefficiency of existing multivariate LTSF Transformers to model series-wise relationships: the characteristic differences between series are often captured incorrectly. To address this, we introduce ARM: a multivariate temporal-contextual adaptive learning method, which is an enhanced architecture specifically designed for multivariate LTSF modelling. ARM employs Adaptive Univariate Effect Learning (AUEL), Random Dropping (RD) training strategy, and Multi-kernel Local Smoothing (MKLS), to better handle individual series temporal patterns and correctly learn inter-series dependencies. ARM demonstrates superior performance on multiple benchmarks without significantly increasing computational costs compared to vanilla Transformer, thereby advancing the state-of-the-art in LTSF. ARM is also generally applicable to other LTSF architecture beyond vanilla Transformer.

Deep Attention Q-Network for Personalized Treatment Recommendation

Tailoring treatment for individual patients is crucial yet challenging in order to achieve optimal healthcare outcomes. Recent advances in reinforcement learning offer promising personalized treatment recommendations; however, they rely solely on current patient observations (vital signs, demographics) as the patient's state, which may not accurately represent the true health status of the patient. This limitation hampers policy learning and evaluation, ultimately limiting treatment effectiveness. In this study, we propose the Deep Attention Q-Network for personalized treatment recommendations, utilizing the Transformer architecture within a deep reinforcement learning framework to efficiently incorporate all past patient observations. We evaluated the model on real-world sepsis and acute hypotension cohorts, demonstrating its superiority to state-of-the-art models. The source code for our model is available at https://github.com/stevenmsm/RL-ICU-DAQN.