On the expressiveness and spectral bias of KANs

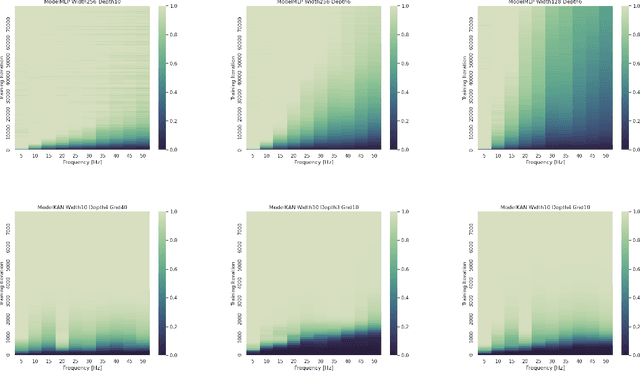
Kolmogorov-Arnold Networks (KAN) \cite{liu2024kan} were very recently proposed as a potential alternative to the prevalent architectural backbone of many deep learning models, the multi-layer perceptron (MLP). KANs have seen success in various tasks of AI for science, with their empirical efficiency and accuracy demostrated in function regression, PDE solving, and many more scientific problems. In this article, we revisit the comparison of KANs and MLPs, with emphasis on a theoretical perspective. On the one hand, we compare the representation and approximation capabilities of KANs and MLPs. We establish that MLPs can be represented using KANs of a comparable size. This shows that the approximation and representation capabilities of KANs are at least as good as MLPs. Conversely, we show that KANs can be represented using MLPs, but that in this representation the number of parameters increases by a factor of the KAN grid size. This suggests that KANs with a large grid size may be more efficient than MLPs at approximating certain functions. On the other hand, from the perspective of learning and optimization, we study the spectral bias of KANs compared with MLPs. We demonstrate that KANs are less biased toward low frequencies than MLPs. We highlight that the multi-level learning feature specific to KANs, i.e. grid extension of splines, improves the learning process for high-frequency components. Detailed comparisons with different choices of depth, width, and grid sizes of KANs are made, shedding some light on how to choose the hyperparameters in practice.

Approximation Rates for Shallow ReLU$^k$ Neural Networks on Sobolev Spaces via the Radon Transform

Let $\Omega\subset \mathbb{R}^d$ be a bounded domain. We consider the problem of how efficiently shallow neural networks with the ReLU$^k$ activation function can approximate functions from Sobolev spaces $W^s(L_p(\Omega))$ with error measured in the $L_q(\Omega)$-norm. Utilizing the Radon transform and recent results from discrepancy theory, we provide a simple proof of nearly optimal approximation rates in a variety of cases, including when $q\leq p$, $p\geq 2$, and $s \leq k + (d+1)/2$. The rates we derive are optimal up to logarithmic factors, and significantly generalize existing results. An interesting consequence is that the adaptivity of shallow ReLU$^k$ neural networks enables them to obtain optimal approximation rates for smoothness up to order $s = k + (d+1)/2$, even though they represent piecewise polynomials of fixed degree $k$.

Equivariant Frames and the Impossibility of Continuous Canonicalization

Canonicalization provides an architecture-agnostic method for enforcing equivariance, with generalizations such as frame-averaging recently gaining prominence as a lightweight and flexible alternative to equivariant architectures. Recent works have found an empirical benefit to using probabilistic frames instead, which learn weighted distributions over group elements. In this work, we provide strong theoretical justification for this phenomenon: for commonly-used groups, there is no efficiently computable choice of frame that preserves continuity of the function being averaged. In other words, unweighted frame-averaging can turn a smooth, non-symmetric function into a discontinuous, symmetric function. To address this fundamental robustness problem, we formally define and construct \emph{weighted} frames, which provably preserve continuity, and demonstrate their utility by constructing efficient and continuous weighted frames for the actions of $SO(2)$, $SO(3)$, and $S_n$ on point clouds.

A qualitative difference between gradient flows of convex functions in finite- and infinite-dimensional Hilbert spaces

We consider gradient flow/gradient descent and heavy ball/accelerated gradient descent optimization for convex objective functions. In the gradient flow case, we prove the following: 1. If $f$ does not have a minimizer, the convergence $f(x_t)\to \inf f$ can be arbitrarily slow. 2. If $f$ does have a minimizer, the excess energy $f(x_t) - \inf f$ is integrable/summable in time. In particular, $f(x_t) - \inf f = o(1/t)$ as $t\to\infty$. 3. In Hilbert spaces, this is optimal: $f(x_t) - \inf f$ can decay to $0$ as slowly as any given function which is monotone decreasing and integrable at $\infty$, even for a fixed quadratic objective. 4. In finite dimension (or more generally, for all gradient flow curves of finite length), this is not optimal: We prove that there are convex monotone decreasing integrable functions $g(t)$ which decrease to zero slower than $f(x_t)-\inf f$ for the gradient flow of any convex function on $\mathbb R^d$. For instance, we show that any gradient flow $x_t$ of a convex function $f$ in finite dimension satisfies $\liminf_{t\to\infty} \big(t\cdot \log^2(t)\cdot \big\{f(x_t) -\inf f\big\}\big)=0$. This improves on the commonly reported $O(1/t)$ rate and provides a sharp characterization of the energy decay law. We also note that it is impossible to establish a rate $O(1/(t\phi(t))$ for any function $\phi$ which satisfies $\lim_{t\to\infty}\phi(t) = \infty$, even asymptotically. Similar results are obtained in related settings for (1) discrete time gradient descent, (2) stochastic gradient descent with multiplicative noise and (3) the heavy ball ODE. In the case of stochastic gradient descent, the summability of $\mathbb E[f(x_n) - \inf f]$ is used to prove that $f(x_n)\to \inf f$ almost surely - an improvement on the convergence almost surely up to a subsequence which follows from the $O(1/n)$ decay estimate.

Optimal Approximation of Zonoids and Uniform Approximation by Shallow Neural Networks

We study the following two related problems. The first is to determine to what error an arbitrary zonoid in $\mathbb{R}^{d+1}$ can be approximated in the Hausdorff distance by a sum of $n$ line segments. The second is to determine optimal approximation rates in the uniform norm for shallow ReLU$^k$ neural networks on their variation spaces. The first of these problems has been solved for $d\neq 2,3$, but when $d=2,3$ a logarithmic gap between the best upper and lower bounds remains. We close this gap, which completes the solution in all dimensions. For the second problem, our techniques significantly improve upon existing approximation rates when $k\geq 1$, and enable uniform approximation of both the target function and its derivatives.

Weighted variation spaces and approximation by shallow ReLU networks

We investigate the approximation of functions $f$ on a bounded domain $\Omega\subset \mathbb{R}^d$ by the outputs of single-hidden-layer ReLU neural networks of width $n$. This form of nonlinear $n$-term dictionary approximation has been intensely studied since it is the simplest case of neural network approximation (NNA). There are several celebrated approximation results for this form of NNA that introduce novel model classes of functions on $\Omega$ whose approximation rates avoid the curse of dimensionality. These novel classes include Barron classes, and classes based on sparsity or variation such as the Radon-domain BV classes. The present paper is concerned with the definition of these novel model classes on domains $\Omega$. The current definition of these model classes does not depend on the domain $\Omega$. A new and more proper definition of model classes on domains is given by introducing the concept of weighted variation spaces. These new model classes are intrinsic to the domain itself. The importance of these new model classes is that they are strictly larger than the classical (domain-independent) classes. Yet, it is shown that they maintain the same NNA rates.

Sharp Convergence Rates for Matching Pursuit

We study the fundamental limits of matching pursuit, or the pure greedy algorithm, for approximating a target function by a sparse linear combination of elements from a dictionary. When the target function is contained in the variation space corresponding to the dictionary, many impressive works over the past few decades have obtained upper and lower bounds on the error of matching pursuit, but they do not match. The main contribution of this paper is to close this gap and obtain a sharp characterization of the decay rate of matching pursuit. Specifically, we construct a worst case dictionary which shows that the existing best upper bound cannot be significantly improved. It turns out that, unlike other greedy algorithm variants, the converge rate is suboptimal and is determined by the solution to a certain non-linear equation. This enables us to conclude that any amount of shrinkage improves matching pursuit in the worst case.

Sharp Lower Bounds on Interpolation by Deep ReLU Neural Networks at Irregularly Spaced Data

We study the interpolation, or memorization, power of deep ReLU neural networks. Specifically, we consider the question of how efficiently, in terms of the number of parameters, deep ReLU networks can interpolate values at $N$ datapoints in the unit ball which are separated by a distance $\delta$. We show that $\Omega(N)$ parameters are required in the regime where $\delta$ is exponentially small in $N$, which gives the sharp result in this regime since $O(N)$ parameters are always sufficient. This also shows that the bit-extraction technique used to prove lower bounds on the VC dimension cannot be applied to irregularly spaced datapoints.

Optimal Approximation Rates for Deep ReLU Neural Networks on Sobolev Spaces

We study the problem of how efficiently, in terms of the number of parameters, deep neural networks with the ReLU activation function can approximate functions in the Sobolev space $W^s(L_q(\Omega))$ on a bounded domain $\Omega$, where the error is measured in $L_p(\Omega)$. This problem is important for studying the application of neural networks in scientific computing and has previously been solved only in the case $p=q=\infty$. Our contribution is to provide a solution for all $1\leq p,q\leq \infty$ and $s > 0$. Our results show that deep ReLU networks significantly outperform classical methods of approximation, but that this comes at the cost of parameters which are not encodable.

On the Activation Function Dependence of the Spectral Bias of Neural Networks

Neural networks are universal function approximators which are known to generalize well despite being dramatically overparameterized. We study this phenomenon from the point of view of the spectral bias of neural networks. Our contributions are two-fold. First, we provide a theoretical explanation for the spectral bias of ReLU neural networks by leveraging connections with the theory of finite element methods. Second, based upon this theory we predict that switching the activation function to a piecewise linear B-spline, namely the Hat function, will remove this spectral bias, which we verify empirically in a variety of settings. Our empirical studies also show that neural networks with the Hat activation function are trained significantly faster using stochastic gradient descent and ADAM. Combined with previous work showing that the Hat activation function also improves generalization accuracy on image classification tasks, this indicates that using the Hat activation provides significant advantages over the ReLU on certain problems.