Optimal Recovery Meets Minimax Estimation

A fundamental problem in statistics and machine learning is to estimate a function $f$ from possibly noisy observations of its point samples. The goal is to design a numerical algorithm to construct an approximation $\hat f$ to $f$ in a prescribed norm that asymptotically achieves the best possible error (as a function of the number $m$ of observations and the variance $\sigma^2$ of the noise). This problem has received considerable attention in both nonparametric statistics (noisy observations) and optimal recovery (noiseless observations). Quantitative bounds require assumptions on $f$, known as model class assumptions. Classical results assume that $f$ is in the unit ball of a Besov space. In nonparametric statistics, the best possible performance of an algorithm for finding $\hat f$ is known as the minimax rate and has been studied in this setting under the assumption that the noise is Gaussian. In optimal recovery, the best possible performance of an algorithm is known as the optimal recovery rate and has also been determined in this setting. While one would expect that the minimax rate recovers the optimal recovery rate when the noise level $\sigma$ tends to zero, it turns out that the current results on minimax rates do not carefully determine the dependence on $\sigma$ and the limit cannot be taken. This paper handles this issue and determines the noise-level-aware (NLA) minimax rates for Besov classes when error is measured in an $L_q$-norm with matching upper and lower bounds. The end result is a reconciliation between minimax rates and optimal recovery rates. The NLA minimax rate continuously depends on the noise level and recovers the optimal recovery rate when $\sigma$ tends to zero.

Neural networks: deep, shallow, or in between?

We give estimates from below for the error of approximation of a compact subset from a Banach space by the outputs of feed-forward neural networks with width W, depth l and Lipschitz activation functions. We show that, modulo logarithmic factors, rates better that entropy numbers' rates are possibly attainable only for neural networks for which the depth l goes to infinity, and that there is no gain if we fix the depth and let the width W go to infinity.

Limitations on approximation by deep and shallow neural networks

We prove Carl's type inequalities for the error of approximation of compact sets K by deep and shallow neural networks. This in turn gives lower bounds on how well we can approximate the functions in K when requiring the approximants to come from outputs of such networks. Our results are obtained as a byproduct of the study of the recently introduced Lipschitz widths.

Optimal Learning

This paper studies the problem of learning an unknown function $f$ from given data about $f$. The learning problem is to give an approximation $\hat f$ to $f$ that predicts the values of $f$ away from the data. There are numerous settings for this learning problem depending on (i) what additional information we have about $f$ (known as a model class assumption), (ii) how we measure the accuracy of how well $\hat f$ predicts $f$, (iii) what is known about the data and data sites, (iv) whether the data observations are polluted by noise. A mathematical description of the optimal performance possible (the smallest possible error of recovery) is known in the presence of a model class assumption. Under standard model class assumptions, it is shown in this paper that a near optimal $\hat f$ can be found by solving a certain discrete over-parameterized optimization problem with a penalty term. Here, near optimal means that the error is bounded by a fixed constant times the optimal error. This explains the advantage of over-parameterization which is commonly used in modern machine learning. The main results of this paper prove that over-parameterized learning with an appropriate loss function gives a near optimal approximation $\hat f$ of the function $f$ from which the data is collected. Quantitative bounds are given for how much over-parameterization needs to be employed and how the penalization needs to be scaled in order to guarantee a near optimal recovery of $f$. An extension of these results to the case where the data is polluted by additive deterministic noise is also given.

Neural Network Approximation of Refinable Functions

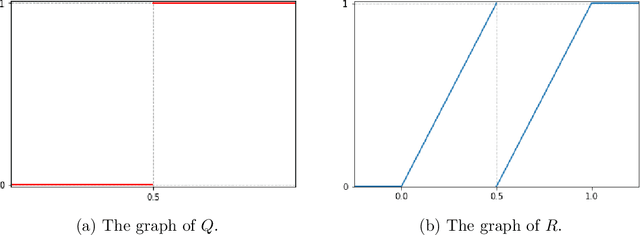
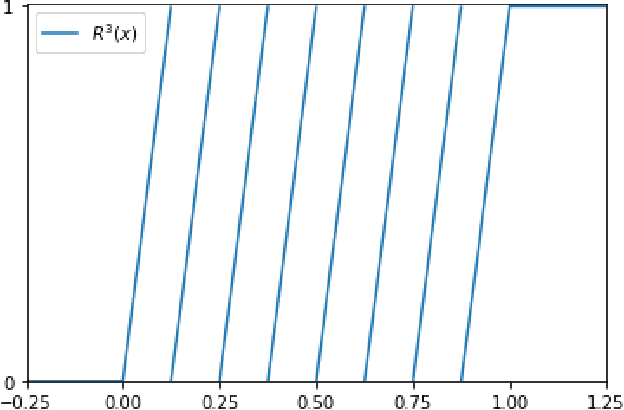
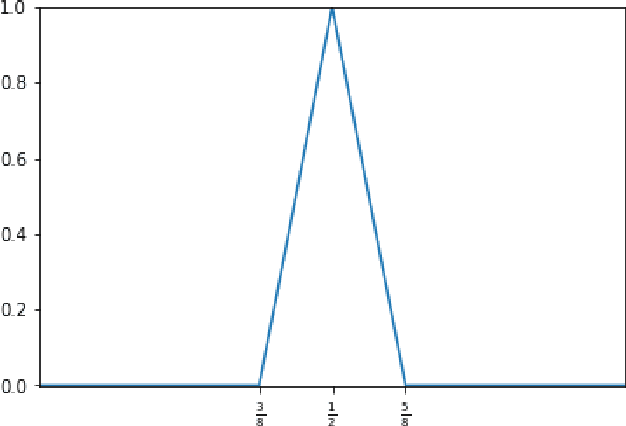
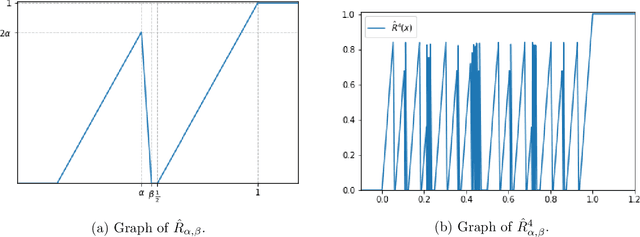
In the desire to quantify the success of neural networks in deep learning and other applications, there is a great interest in understanding which functions are efficiently approximated by the outputs of neural networks. By now, there exists a variety of results which show that a wide range of functions can be approximated with sometimes surprising accuracy by these outputs. For example, it is known that the set of functions that can be approximated with exponential accuracy (in terms of the number of parameters used) includes, on one hand, very smooth functions such as polynomials and analytic functions (see e.g. \cite{E,S,Y}) and, on the other hand, very rough functions such as the Weierstrass function (see e.g. \cite{EPGB,DDFHP}), which is nowhere differentiable. In this paper, we add to the latter class of rough functions by showing that it also includes refinable functions. Namely, we show that refinable functions are approximated by the outputs of deep ReLU networks with a fixed width and increasing depth with accuracy exponential in terms of their number of parameters. Our results apply to functions used in the standard construction of wavelets as well as to functions constructed via subdivision algorithms in Computer Aided Geometric Design.