Optimal Recovery Meets Minimax Estimation

A fundamental problem in statistics and machine learning is to estimate a function $f$ from possibly noisy observations of its point samples. The goal is to design a numerical algorithm to construct an approximation $\hat f$ to $f$ in a prescribed norm that asymptotically achieves the best possible error (as a function of the number $m$ of observations and the variance $\sigma^2$ of the noise). This problem has received considerable attention in both nonparametric statistics (noisy observations) and optimal recovery (noiseless observations). Quantitative bounds require assumptions on $f$, known as model class assumptions. Classical results assume that $f$ is in the unit ball of a Besov space. In nonparametric statistics, the best possible performance of an algorithm for finding $\hat f$ is known as the minimax rate and has been studied in this setting under the assumption that the noise is Gaussian. In optimal recovery, the best possible performance of an algorithm is known as the optimal recovery rate and has also been determined in this setting. While one would expect that the minimax rate recovers the optimal recovery rate when the noise level $\sigma$ tends to zero, it turns out that the current results on minimax rates do not carefully determine the dependence on $\sigma$ and the limit cannot be taken. This paper handles this issue and determines the noise-level-aware (NLA) minimax rates for Besov classes when error is measured in an $L_q$-norm with matching upper and lower bounds. The end result is a reconciliation between minimax rates and optimal recovery rates. The NLA minimax rate continuously depends on the noise level and recovers the optimal recovery rate when $\sigma$ tends to zero.

The Effects of Multi-Task Learning on ReLU Neural Network Functions

This paper studies the properties of solutions to multi-task shallow ReLU neural network learning problems, wherein the network is trained to fit a dataset with minimal sum of squared weights. Remarkably, the solutions learned for each individual task resemble those obtained by solving a kernel method, revealing a novel connection between neural networks and kernel methods. It is known that single-task neural network training problems are equivalent to minimum norm interpolation problem in a non-Hilbertian Banach space, and that the solutions of such problems are generally non-unique. In contrast, we prove that the solutions to univariate-input, multi-task neural network interpolation problems are almost always unique, and coincide with the solution to a minimum-norm interpolation problem in a Sobolev (Reproducing Kernel) Hilbert Space. We also demonstrate a similar phenomenon in the multivariate-input case; specifically, we show that neural network learning problems with large numbers of diverse tasks are approximately equivalent to an $\ell^2$ (Hilbert space) minimization problem over a fixed kernel determined by the optimal neurons.

ReLUs Are Sufficient for Learning Implicit Neural Representations

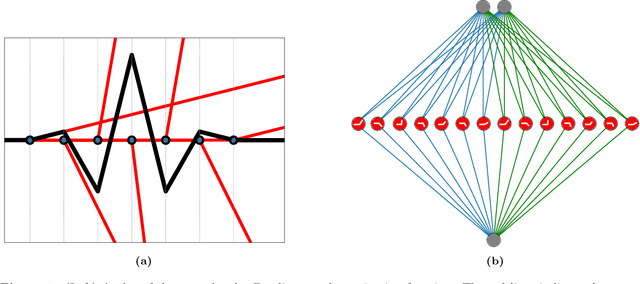
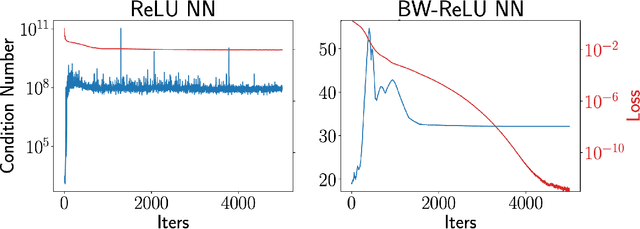
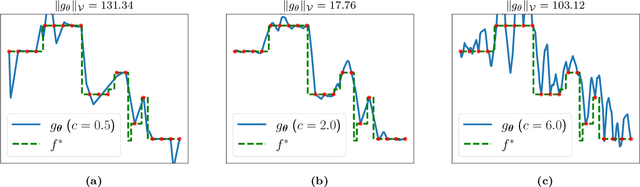
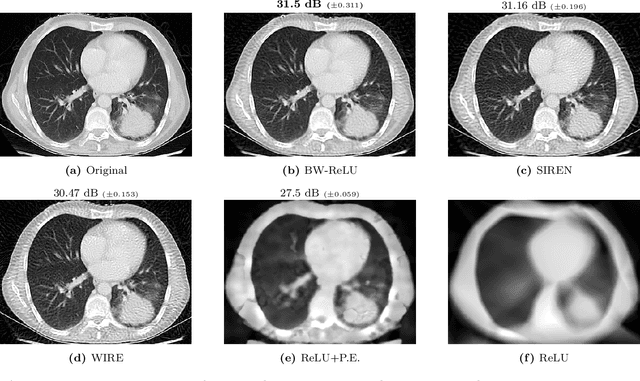
Motivated by the growing theoretical understanding of neural networks that employ the Rectified Linear Unit (ReLU) as their activation function, we revisit the use of ReLU activation functions for learning implicit neural representations (INRs). Inspired by second order B-spline wavelets, we incorporate a set of simple constraints to the ReLU neurons in each layer of a deep neural network (DNN) to remedy the spectral bias. This in turn enables its use for various INR tasks. Empirically, we demonstrate that, contrary to popular belief, one can learn state-of-the-art INRs based on a DNN composed of only ReLU neurons. Next, by leveraging recent theoretical works which characterize the kinds of functions ReLU neural networks learn, we provide a way to quantify the regularity of the learned function. This offers a principled approach to selecting the hyperparameters in INR architectures. We substantiate our claims through experiments in signal representation, super resolution, and computed tomography, demonstrating the versatility and effectiveness of our method. The code for all experiments can be found at https://github.com/joeshenouda/relu-inrs.

An Experimental Design Framework for Label-Efficient Supervised Finetuning of Large Language Models

Supervised finetuning (SFT) on instruction datasets has played a crucial role in achieving the remarkable zero-shot generalization capabilities observed in modern large language models (LLMs). However, the annotation efforts required to produce high quality responses for instructions are becoming prohibitively expensive, especially as the number of tasks spanned by instruction datasets continues to increase. Active learning is effective in identifying useful subsets of samples to annotate from an unlabeled pool, but its high computational cost remains a barrier to its widespread applicability in the context of LLMs. To mitigate the annotation cost of SFT and circumvent the computational bottlenecks of active learning, we propose using experimental design. Experimental design techniques select the most informative samples to label, and typically maximize some notion of uncertainty and/or diversity. In our work, we implement a framework that evaluates several existing and novel experimental design techniques and find that these methods consistently yield significant gains in label efficiency with little computational overhead. On generative tasks, our methods achieve the same generalization performance with only $50\%$ of annotation cost required by random sampling.

Weighted variation spaces and approximation by shallow ReLU networks

We investigate the approximation of functions $f$ on a bounded domain $\Omega\subset \mathbb{R}^d$ by the outputs of single-hidden-layer ReLU neural networks of width $n$. This form of nonlinear $n$-term dictionary approximation has been intensely studied since it is the simplest case of neural network approximation (NNA). There are several celebrated approximation results for this form of NNA that introduce novel model classes of functions on $\Omega$ whose approximation rates avoid the curse of dimensionality. These novel classes include Barron classes, and classes based on sparsity or variation such as the Radon-domain BV classes. The present paper is concerned with the definition of these novel model classes on domains $\Omega$. The current definition of these model classes does not depend on the domain $\Omega$. A new and more proper definition of model classes on domains is given by introducing the concept of weighted variation spaces. These new model classes are intrinsic to the domain itself. The importance of these new model classes is that they are strictly larger than the classical (domain-independent) classes. Yet, it is shown that they maintain the same NNA rates.

Vector-Valued Variation Spaces and Width Bounds for DNNs: Insights on Weight Decay Regularization

Deep neural networks (DNNs) trained to minimize a loss term plus the sum of squared weights via gradient descent corresponds to the common approach of training with weight decay. This paper provides new insights into this common learning framework. We characterize the kinds of functions learned by training with weight decay for multi-output (vector-valued) ReLU neural networks. This extends previous characterizations that were limited to single-output (scalar-valued) networks. This characterization requires the definition of a new class of neural function spaces that we call vector-valued variation (VV) spaces. We prove that neural networks (NNs) are optimal solutions to learning problems posed over VV spaces via a novel representer theorem. This new representer theorem shows that solutions to these learning problems exist as vector-valued neural networks with widths bounded in terms of the number of training data. Next, via a novel connection to the multi-task lasso problem, we derive new and tighter bounds on the widths of homogeneous layers in DNNs. The bounds are determined by the effective dimensions of the training data embeddings in/out of the layers. This result sheds new light on the architectural requirements for DNNs. Finally, the connection to the multi-task lasso problem suggests a new approach to compressing pre-trained networks.

Filtered Iterative Denoising for Linear Inverse Problems

Iterative denoising algorithms (IDAs) have been tremendously successful in a range of linear inverse problems arising in signal and image processing. The classic instance of this is the famous Iterative Soft-Thresholding Algorithm (ISTA), based on soft-thresholding of wavelet coefficients. More modern approaches to IDAs replace soft-thresholding with a black-box denoiser, such as BM3D or a learned deep neural network denoiser. These are often referred to as ``plug-and-play" (PnP) methods because, in principle, an off-the-shelf denoiser can be used for a variety of different inverse problems. The problem with PnP methods is that they may not provide the best solutions to a specific linear inverse problem; better solutions can often be obtained by a denoiser that is customized to the problem domain. A problem-specific denoiser, however, requires expensive re-engineering or re-learning which eliminates the simplicity and ease that makes PnP methods attractive in the first place. This paper proposes a new IDA that allows one to use a general, black-box denoiser more effectively via a simple linear filtering modification to the usual gradient update steps that accounts for the specific linear inverse problem. The proposed Filtered IDA (FIDA) is mathematically derived from the classical ISTA and wavelet denoising viewpoint. We show experimentally that FIDA can produce superior results compared to existing IDA methods with BM3D.

Deep Learning Meets Sparse Regularization: A Signal Processing Perspective

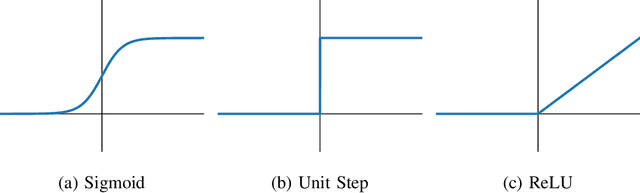
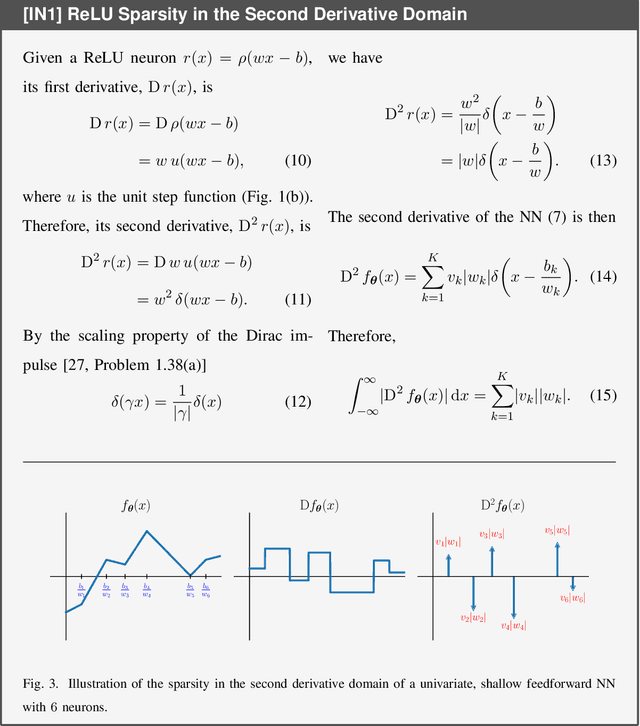
Deep learning has been wildly successful in practice and most state-of-the-art machine learning methods are based on neural networks. Lacking, however, is a rigorous mathematical theory that adequately explains the amazing performance of deep neural networks. In this article, we present a relatively new mathematical framework that provides the beginning of a deeper understanding of deep learning. This framework precisely characterizes the functional properties of neural networks that are trained to fit to data. The key mathematical tools which support this framework include transform-domain sparse regularization, the Radon transform of computed tomography, and approximation theory, which are all techniques deeply rooted in signal processing. This framework explains the effect of weight decay regularization in neural network training, the use of skip connections and low-rank weight matrices in network architectures, the role of sparsity in neural networks, and explains why neural networks can perform well in high-dimensional problems.

A Better Way to Decay: Proximal Gradient Training Algorithms for Neural Nets

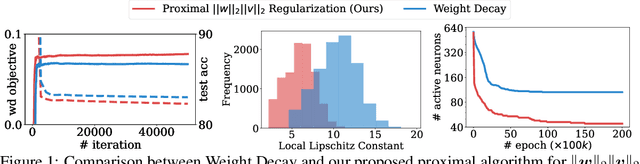
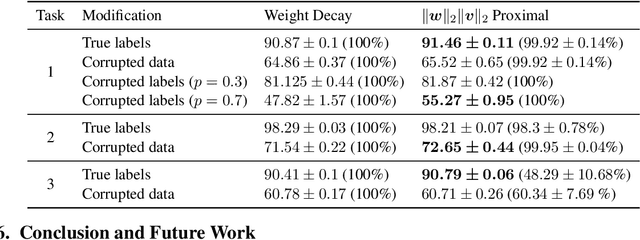
Weight decay is one of the most widely used forms of regularization in deep learning, and has been shown to improve generalization and robustness. The optimization objective driving weight decay is a sum of losses plus a term proportional to the sum of squared weights. This paper argues that stochastic gradient descent (SGD) may be an inefficient algorithm for this objective. For neural networks with ReLU activations, solutions to the weight decay objective are equivalent to those of a different objective in which the regularization term is instead a sum of products of $\ell_2$ (not squared) norms of the input and output weights associated each ReLU. This alternative (and effectively equivalent) regularization suggests a novel proximal gradient algorithm for network training. Theory and experiments support the new training approach, showing that it can converge much faster to the sparse solutions it shares with standard weight decay training.

Near-Minimax Optimal Estimation With Shallow ReLU Neural Networks

We study the problem of estimating an unknown function from noisy data using shallow (single-hidden layer) ReLU neural networks. The estimators we study minimize the sum of squared data-fitting errors plus a regularization term proportional to the Euclidean norm of the network weights. This minimization corresponds to the common approach of training a neural network with weight decay. We quantify the performance (mean-squared error) of these neural network estimators when the data-generating function belongs to the space of functions of second-order bounded variation in the Radon domain. This space of functions was recently proposed as the natural function space associated with shallow ReLU neural networks. We derive a minimax lower bound for the estimation problem for this function space and show that the neural network estimators are minimax optimal up to logarithmic factors. We also show that this is a "mixed variation" function space that contains classical multivariate function spaces including certain Sobolev spaces and certain spectral Barron spaces. Finally, we use these results to quantify a gap between neural networks and linear methods (which include kernel methods). This paper sheds light on the phenomenon that neural networks seem to break the curse of dimensionality.