Online Finetuning Decision Transformers with Pure RL Gradients

Decision Transformers (DTs) have emerged as a powerful framework for sequential decision making by formulating offline reinforcement learning (RL) as a sequence modeling problem. However, extending DTs to online settings with pure RL gradients remains largely unexplored, as existing approaches continue to rely heavily on supervised sequence-modeling objectives during online finetuning. We identify hindsight return relabeling -- a standard component in online DTs -- as a critical obstacle to RL-based finetuning: while beneficial for supervised learning, it is fundamentally incompatible with importance sampling-based RL algorithms such as GRPO, leading to unstable training. Building on this insight, we propose new algorithms that enable online finetuning of Decision Transformers using pure reinforcement learning gradients. We adapt GRPO to DTs and introduce several key modifications, including sub-trajectory optimization for improved credit assignment, sequence-level likelihood objectives for enhanced stability and efficiency, and active sampling to encourage exploration in uncertain regions. Through extensive experiments, we demonstrate that our methods outperform existing online DT baselines and achieve new state-of-the-art performance across multiple benchmarks, highlighting the effectiveness of pure-RL-based online finetuning for Decision Transformers.

Interactive Machine Learning: From Theory to Scale

Machine learning has achieved remarkable success across a wide range of applications, yet many of its most effective methods rely on access to large amounts of labeled data or extensive online interaction. In practice, acquiring high-quality labels and making decisions through trial-and-error can be expensive, time-consuming, or risky, particularly in large-scale or high-stakes settings. This dissertation studies interactive machine learning, in which the learner actively influences how information is collected or which actions are taken, using past observations to guide future interactions. We develop new algorithmic principles and establish fundamental limits for interactive learning along three dimensions: active learning with noisy data and rich model classes, sequential decision making with large action spaces, and model selection under partial feedback. Our results include the first computationally efficient active learning algorithms achieving exponential label savings without low-noise assumptions; the first efficient, general-purpose contextual bandit algorithms whose guarantees are independent of the size of the action space; and the first tight characterizations of the fundamental cost of model selection in sequential decision making. Overall, this dissertation advances the theoretical foundations of interactive learning by developing algorithms that are statistically optimal and computationally efficient, while also providing principled guidance for deploying interactive learning methods in large-scale, real-world settings.

Strategic Scaling of Test-Time Compute: A Bandit Learning Approach

Scaling test-time compute has emerged as an effective strategy for improving the performance of large language models. However, existing methods typically allocate compute uniformly across all queries, overlooking variation in query difficulty. To address this inefficiency, we formulate test-time compute allocation as a novel bandit learning problem and propose adaptive algorithms that estimate query difficulty on the fly and allocate compute accordingly. Compared to uniform allocation, our algorithms allocate more compute to challenging queries while maintaining accuracy on easier ones. Among challenging queries, our algorithms further learn to prioritize solvable instances, effectively reducing excessive computing on unsolvable queries. We theoretically prove that our algorithms achieve better compute efficiency than uniform allocation and empirically validate their effectiveness on math and code benchmarks. Specifically, our algorithms achieve up to an 11.10% performance improvement (15.04% relative) on the MATH-500 dataset and up to a 7.41% performance improvement (14.40% relative) on LiveCodeBench.

Mixtraining: A Better Trade-Off Between Compute and Performance

Incorporating self-supervised learning (SSL) before standard supervised learning (SL) has become a widely used strategy to enhance model performance, particularly in data-limited scenarios. However, this approach introduces a trade-off between computation and performance: while SSL helps with representation learning, it requires a separate, often time-consuming training phase, increasing computational overhead and limiting efficiency in resource-constrained settings. To address these challenges, we propose MixTraining, a novel framework that interleaves several SSL and SL epochs within a unified mixtraining training phase, featuring a smooth transition between two learning objectives. MixTraining enhances synergy between SSL and SL for improved accuracy and consolidates shared computation steps to reduce computation overhead. MixTraining is versatile and applicable to both single-task and multi-task learning scenarios. Extensive experiments demonstrate that MixTraining offers a superior compute-performance trade-off compared to conventional pipelines, achieving an 8.81% absolute accuracy gain (18.89% relative accuracy gain) on the TinyImageNet dataset while accelerating training by up to 1.29x with the ViT-Tiny model.

Efficient Sparse PCA via Block-Diagonalization

Sparse Principal Component Analysis (Sparse PCA) is a pivotal tool in data analysis and dimensionality reduction. However, Sparse PCA is a challenging problem in both theory and practice: it is known to be NP-hard and current exact methods generally require exponential runtime. In this paper, we propose a novel framework to efficiently approximate Sparse PCA by (i) approximating the general input covariance matrix with a re-sorted block-diagonal matrix, (ii) solving the Sparse PCA sub-problem in each block, and (iii) reconstructing the solution to the original problem. Our framework is simple and powerful: it can leverage any off-the-shelf Sparse PCA algorithm and achieve significant computational speedups, with a minor additive error that is linear in the approximation error of the block-diagonal matrix. Suppose $g(k, d)$ is the runtime of an algorithm (approximately) solving Sparse PCA in dimension $d$ and with sparsity value $k$. Our framework, when integrated with this algorithm, reduces the runtime to $\mathcal{O}\left(\frac{d}{d^\star} \cdot g(k, d^\star) + d^2\right)$, where $d^\star \leq d$ is the largest block size of the block-diagonal matrix. For instance, integrating our framework with the Branch-and-Bound algorithm reduces the complexity from $g(k, d) = \mathcal{O}(k^3\cdot d^k)$ to $\mathcal{O}(k^3\cdot d \cdot (d^\star)^{k-1})$, demonstrating exponential speedups if $d^\star$ is small. We perform large-scale evaluations on many real-world datasets: for exact Sparse PCA algorithm, our method achieves an average speedup factor of 93.77, while maintaining an average approximation error of 2.15%; for approximate Sparse PCA algorithm, our method achieves an average speedup factor of 6.77 and an average approximation error of merely 0.37%.

Efficient Sequential Decision Making with Large Language Models

This paper focuses on extending the success of large language models (LLMs) to sequential decision making. Existing efforts either (i) re-train or finetune LLMs for decision making, or (ii) design prompts for pretrained LLMs. The former approach suffers from the computational burden of gradient updates, and the latter approach does not show promising results. In this paper, we propose a new approach that leverages online model selection algorithms to efficiently incorporate LLMs agents into sequential decision making. Statistically, our approach significantly outperforms both traditional decision making algorithms and vanilla LLM agents. Computationally, our approach avoids the need for expensive gradient updates of LLMs, and throughout the decision making process, it requires only a small number of LLM calls. We conduct extensive experiments to verify the effectiveness of our proposed approach. As an example, on a large-scale Amazon dataset, our approach achieves more than a $6$x performance gain over baselines while calling LLMs in only $1.5$\% of the time steps.

An Experimental Design Framework for Label-Efficient Supervised Finetuning of Large Language Models

Supervised finetuning (SFT) on instruction datasets has played a crucial role in achieving the remarkable zero-shot generalization capabilities observed in modern large language models (LLMs). However, the annotation efforts required to produce high quality responses for instructions are becoming prohibitively expensive, especially as the number of tasks spanned by instruction datasets continues to increase. Active learning is effective in identifying useful subsets of samples to annotate from an unlabeled pool, but its high computational cost remains a barrier to its widespread applicability in the context of LLMs. To mitigate the annotation cost of SFT and circumvent the computational bottlenecks of active learning, we propose using experimental design. Experimental design techniques select the most informative samples to label, and typically maximize some notion of uncertainty and/or diversity. In our work, we implement a framework that evaluates several existing and novel experimental design techniques and find that these methods consistently yield significant gains in label efficiency with little computational overhead. On generative tasks, our methods achieve the same generalization performance with only $50\%$ of annotation cost required by random sampling.

LabelBench: A Comprehensive Framework for Benchmarking Label-Efficient Learning

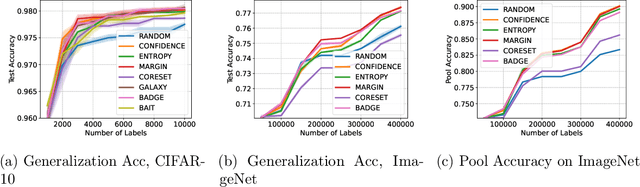
Labeled data are critical to modern machine learning applications, but obtaining labels can be expensive. To mitigate this cost, machine learning methods, such as transfer learning, semi-supervised learning and active learning, aim to be label-efficient: achieving high predictive performance from relatively few labeled examples. While obtaining the best label-efficiency in practice often requires combinations of these techniques, existing benchmark and evaluation frameworks do not capture a concerted combination of all such techniques. This paper addresses this deficiency by introducing LabelBench, a new computationally-efficient framework for joint evaluation of multiple label-efficient learning techniques. As an application of LabelBench, we introduce a novel benchmark of state-of-the-art active learning methods in combination with semi-supervised learning for fine-tuning pretrained vision transformers. Our benchmark demonstrates better label-efficiencies than previously reported in active learning. LabelBench's modular codebase is open-sourced for the broader community to contribute label-efficient learning methods and benchmarks. The repository can be found at: https://github.com/EfficientTraining/LabelBench.

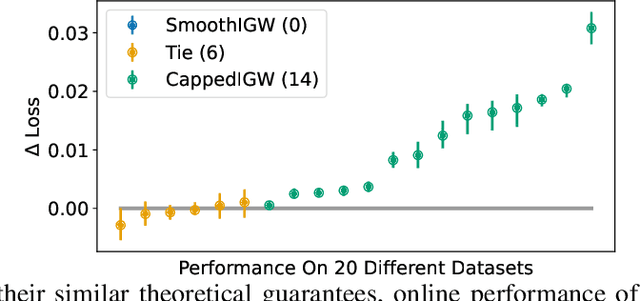
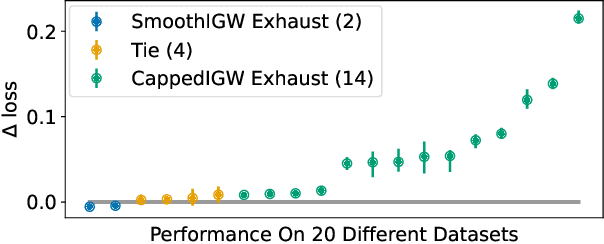
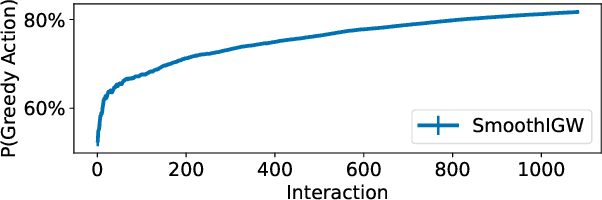
Infinite Action Contextual Bandits with Reusable Data Exhaust

For infinite action contextual bandits, smoothed regret and reduction to regression results in state-of-the-art online statistical performance with computational cost independent of the action set: unfortunately, the resulting data exhaust does not have well-defined importance-weights. This frustrates the execution of downstream data science processes such as offline model selection. In this paper we describe an online algorithm with an equivalent smoothed regret guarantee, but which generates well-defined importance weights: in exchange, the online computational cost increases, but only to order smoothness (i.e., still independent of the action set). This removes a key obstacle to adoption of smoothed regret in production scenarios.

Active Learning with Neural Networks: Insights from Nonparametric Statistics

Deep neural networks have great representation power, but typically require large numbers of training examples. This motivates deep active learning methods that can significantly reduce the amount of labeled training data. Empirical successes of deep active learning have been recently reported in the literature, however, rigorous label complexity guarantees of deep active learning have remained elusive. This constitutes a significant gap between theory and practice. This paper tackles this gap by providing the first near-optimal label complexity guarantees for deep active learning. The key insight is to study deep active learning from the nonparametric classification perspective. Under standard low noise conditions, we show that active learning with neural networks can provably achieve the minimax label complexity, up to disagreement coefficient and other logarithmic terms. When equipped with an abstention option, we further develop an efficient deep active learning algorithm that achieves $\mathsf{polylog}(\frac{1}{\epsilon})$ label complexity, without any low noise assumptions. We also provide extensions of our results beyond the commonly studied Sobolev/H\"older spaces and develop label complexity guarantees for learning in Radon $\mathsf{BV}^2$ spaces, which have recently been proposed as natural function spaces associated with neural networks.