Reinforcement Learning with Euclidean Data Augmentation for State-Based Continuous Control

Data augmentation creates new data points by transforming the original ones for a reinforcement learning (RL) agent to learn from, which has been shown to be effective for the objective of improving the data efficiency of RL for continuous control. Prior work towards this objective has been largely restricted to perturbation-based data augmentation where new data points are created by perturbing the original ones, which has been impressively effective for tasks where the RL agent observes control states as images with perturbations including random cropping, shifting, etc. This work focuses on state-based control, where the RL agent can directly observe raw kinematic and task features, and considers an alternative data augmentation applied to these features based on Euclidean symmetries under transformations like rotations. We show that the default state features used in exiting benchmark tasks that are based on joint configurations are not amenable to Euclidean transformations. We therefore advocate using state features based on configurations of the limbs (i.e., the rigid bodies connected by the joints) that instead provide rich augmented data under Euclidean transformations. With minimal hyperparameter tuning, we show this new Euclidean data augmentation strategy significantly improves both data efficiency and asymptotic performance of RL on a wide range of continuous control tasks.

Efficient Sequential Decision Making with Large Language Models

This paper focuses on extending the success of large language models (LLMs) to sequential decision making. Existing efforts either (i) re-train or finetune LLMs for decision making, or (ii) design prompts for pretrained LLMs. The former approach suffers from the computational burden of gradient updates, and the latter approach does not show promising results. In this paper, we propose a new approach that leverages online model selection algorithms to efficiently incorporate LLMs agents into sequential decision making. Statistically, our approach significantly outperforms both traditional decision making algorithms and vanilla LLM agents. Computationally, our approach avoids the need for expensive gradient updates of LLMs, and throughout the decision making process, it requires only a small number of LLM calls. We conduct extensive experiments to verify the effectiveness of our proposed approach. As an example, on a large-scale Amazon dataset, our approach achieves more than a $6$x performance gain over baselines while calling LLMs in only $1.5$\% of the time steps.

${\rm E}$-Equivariant Actor-Critic Methods for Cooperative Multi-Agent Reinforcement Learning

Identification and analysis of symmetrical patterns in the natural world have led to significant discoveries across various scientific fields, such as the formulation of gravitational laws in physics and advancements in the study of chemical structures. In this paper, we focus on exploiting Euclidean symmetries inherent in certain cooperative multi-agent reinforcement learning (MARL) problems and prevalent in many applications. We begin by formally characterizing a subclass of Markov games with a general notion of symmetries that admits the existence of symmetric optimal values and policies. Motivated by these properties, we design neural network architectures with symmetric constraints embedded as an inductive bias for multi-agent actor-critic methods. This inductive bias results in superior performance in various cooperative MARL benchmarks and impressive generalization capabilities such as zero-shot learning and transfer learning in unseen scenarios with repeated symmetric patterns. The code is available at: https://github.com/dchen48/E3AC.

Context-Aware Bayesian Network Actor-Critic Methods for Cooperative Multi-Agent Reinforcement Learning

Executing actions in a correlated manner is a common strategy for human coordination that often leads to better cooperation, which is also potentially beneficial for cooperative multi-agent reinforcement learning (MARL). However, the recent success of MARL relies heavily on the convenient paradigm of purely decentralized execution, where there is no action correlation among agents for scalability considerations. In this work, we introduce a Bayesian network to inaugurate correlations between agents' action selections in their joint policy. Theoretically, we establish a theoretical justification for why action dependencies are beneficial by deriving the multi-agent policy gradient formula under such a Bayesian network joint policy and proving its global convergence to Nash equilibria under tabular softmax policy parameterization in cooperative Markov games. Further, by equipping existing MARL algorithms with a recent method of differentiable directed acyclic graphs (DAGs), we develop practical algorithms to learn the context-aware Bayesian network policies in scenarios with partial observability and various difficulty. We also dynamically decrease the sparsity of the learned DAG throughout the training process, which leads to weakly or even purely independent policies for decentralized execution. Empirical results on a range of MARL benchmarks show the benefits of our approach.

Convergence and Price of Anarchy Guarantees of the Softmax Policy Gradient in Markov Potential Games

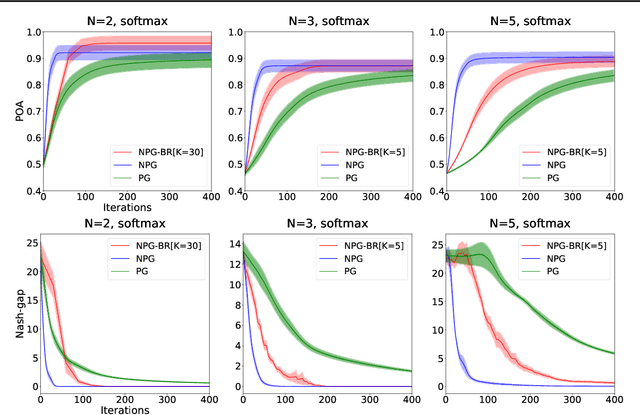
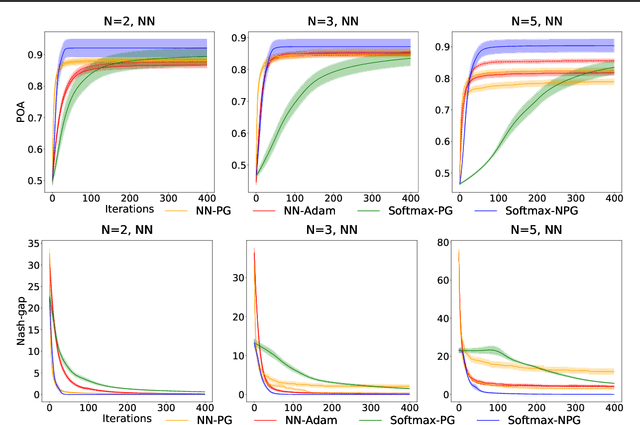
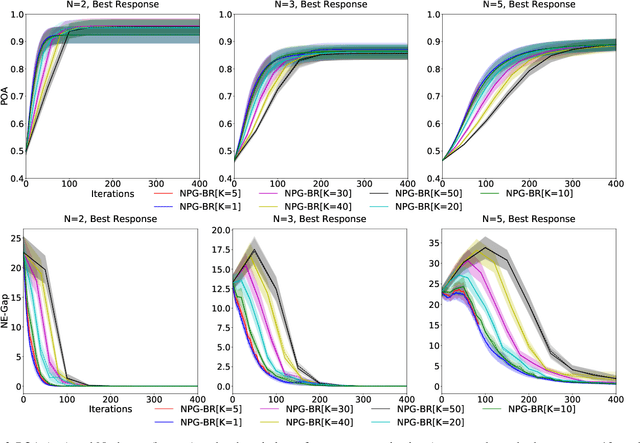
We study the performance of policy gradient methods for the subclass of Markov games known as Markov potential games (MPGs), which extends the notion of normal-form potential games to the stateful setting and includes the important special case of the fully cooperative setting where the agents share an identical reward function. Our focus in this paper is to study the convergence of the policy gradient method for solving MPGs under softmax policy parameterization, both tabular and parameterized with general function approximators such as neural networks. We first show the asymptotic convergence of this method to a Nash equilibrium of MPGs for tabular softmax policies. Second, we derive the finite-time performance of the policy gradient in two settings: 1) using the log-barrier regularization, and 2) using the natural policy gradient under the best-response dynamics (NPG-BR). Finally, extending the notion of price of anarchy (POA) and smoothness in normal-form games, we introduce the POA for MPGs and provide a POA bound for NPG-BR. To our knowledge, this is the first POA bound for solving MPGs. To support our theoretical results, we empirically compare the convergence rates and POA of policy gradient variants for both tabular and neural softmax policies.

Communication-Efficient Actor-Critic Methods for Homogeneous Markov Games

Recent success in cooperative multi-agent reinforcement learning (MARL) relies on centralized training and policy sharing. Centralized training eliminates the issue of non-stationarity MARL yet induces large communication costs, and policy sharing is empirically crucial to efficient learning in certain tasks yet lacks theoretical justification. In this paper, we formally characterize a subclass of cooperative Markov games where agents exhibit a certain form of homogeneity such that policy sharing provably incurs no suboptimality. This enables us to develop the first consensus-based decentralized actor-critic method where the consensus update is applied to both the actors and the critics while ensuring convergence. We also develop practical algorithms based on our decentralized actor-critic method to reduce the communication cost during training, while still yielding policies comparable with centralized training.