Thinh T. Doan
Accelerating Multi-Task Temporal Difference Learning under Low-Rank Representation
Mar 03, 2025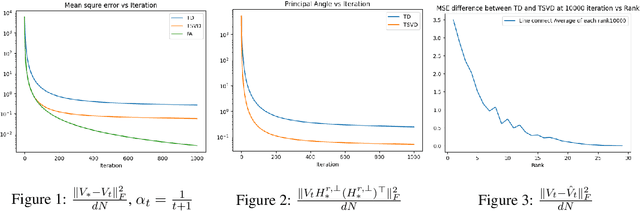
Abstract:We study policy evaluation problems in multi-task reinforcement learning (RL) under a low-rank representation setting. In this setting, we are given $N$ learning tasks where the corresponding value function of these tasks lie in an $r$-dimensional subspace, with $r<N$. One can apply the classic temporal-difference (TD) learning method for solving these problems where this method learns the value function of each task independently. In this paper, we are interested in understanding whether one can exploit the low-rank structure of the multi-task setting to accelerate the performance of TD learning. To answer this question, we propose a new variant of TD learning method, where we integrate the so-called truncated singular value decomposition step into the update of TD learning. This additional step will enable TD learning to exploit the dominant directions due to the low rank structure to update the iterates, therefore, improving its performance. Our empirical results show that the proposed method significantly outperforms the classic TD learning, where the performance gap increases as the rank $r$ decreases. From the theoretical point of view, introducing the truncated singular value decomposition step into TD learning might cause an instability on the updates. We provide a theoretical result showing that the instability does not happen. Specifically, we prove that the proposed method converges at a rate $\mathcal{O}(\frac{\ln(t)}{t})$, where $t$ is the number of iterations. This rate matches that of the standard TD learning.
Bayesian meta learning for trustworthy uncertainty quantification
Jul 27, 2024Abstract:We consider the problem of Bayesian regression with trustworthy uncertainty quantification. We define that the uncertainty quantification is trustworthy if the ground truth can be captured by intervals dependent on the predictive distributions with a pre-specified probability. Furthermore, we propose, Trust-Bayes, a novel optimization framework for Bayesian meta learning which is cognizant of trustworthy uncertainty quantification without explicit assumptions on the prior model/distribution of the functions. We characterize the lower bounds of the probabilities of the ground truth being captured by the specified intervals and analyze the sample complexity with respect to the feasible probability for trustworthy uncertainty quantification. Monte Carlo simulation of a case study using Gaussian process regression is conducted for verification and comparison with the Meta-prior algorithm.
Fast Two-Time-Scale Stochastic Gradient Method with Applications in Reinforcement Learning
May 15, 2024

Abstract:Two-time-scale optimization is a framework introduced in Zeng et al. (2024) that abstracts a range of policy evaluation and policy optimization problems in reinforcement learning (RL). Akin to bi-level optimization under a particular type of stochastic oracle, the two-time-scale optimization framework has an upper level objective whose gradient evaluation depends on the solution of a lower level problem, which is to find the root of a strongly monotone operator. In this work, we propose a new method for solving two-time-scale optimization that achieves significantly faster convergence than the prior arts. The key idea of our approach is to leverage an averaging step to improve the estimates of the operators in both lower and upper levels before using them to update the decision variables. These additional averaging steps eliminate the direct coupling between the main variables, enabling the accelerated performance of our algorithm. We characterize the finite-time convergence rates of the proposed algorithm under various conditions of the underlying objective function, including strong convexity, convexity, Polyak-Lojasiewicz condition, and general non-convexity. These rates significantly improve over the best-known complexity of the standard two-time-scale stochastic approximation algorithm. When applied to RL, we show how the proposed algorithm specializes to novel online sample-based methods that surpass or match the performance of the existing state of the art. Finally, we support our theoretical results with numerical simulations in RL.
Natural Policy Gradient and Actor Critic Methods for Constrained Multi-Task Reinforcement Learning
May 03, 2024

Abstract:Multi-task reinforcement learning (RL) aims to find a single policy that effectively solves multiple tasks at the same time. This paper presents a constrained formulation for multi-task RL where the goal is to maximize the average performance of the policy across tasks subject to bounds on the performance in each task. We consider solving this problem both in the centralized setting, where information for all tasks is accessible to a single server, and in the decentralized setting, where a network of agents, each given one task and observing local information, cooperate to find the solution of the globally constrained objective using local communication. We first propose a primal-dual algorithm that provably converges to the globally optimal solution of this constrained formulation under exact gradient evaluations. When the gradient is unknown, we further develop a sampled-based actor-critic algorithm that finds the optimal policy using online samples of state, action, and reward. Finally, we study the extension of the algorithm to the linear function approximation setting.
Fast Nonlinear Two-Time-Scale Stochastic Approximation: Achieving $O(1/k)$ Finite-Sample Complexity
Jan 24, 2024Abstract:This paper proposes to develop a new variant of the two-time-scale stochastic approximation to find the roots of two coupled nonlinear operators, assuming only noisy samples of these operators can be observed. Our key idea is to leverage the classic Ruppert-Polyak averaging technique to dynamically estimate the operators through their samples. The estimated values of these averaging steps will then be used in the two-time-scale stochastic approximation updates to find the desired solution. Our main theoretical result is to show that under the strongly monotone condition of the underlying nonlinear operators the mean-squared errors of the iterates generated by the proposed method converge to zero at an optimal rate $O(1/k)$, where $k$ is the number of iterations. Our result significantly improves the existing result of two-time-scale stochastic approximation, where the best known finite-time convergence rate is $O(1/k^{2/3})$.
Connected Superlevel Set in (Deep) Reinforcement Learning and its Application to Minimax Theorems
Mar 23, 2023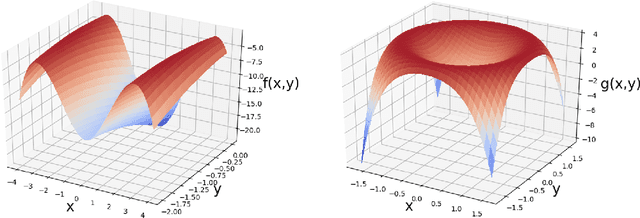
Abstract:The aim of this paper is to improve the understanding of the optimization landscape for policy optimization problems in reinforcement learning. Specifically, we show that the superlevel set of the objective function with respect to the policy parameter is always a connected set both in the tabular setting and under policies represented by a class of neural networks. In addition, we show that the optimization objective as a function of the policy parameter and reward satisfies a stronger "equiconnectedness" property. To our best knowledge, these are novel and previously unknown discoveries. We present an application of the connectedness of these superlevel sets to the derivation of minimax theorems for robust reinforcement learning. We show that any minimax optimization program which is convex on one side and is equiconnected on the other side observes the minimax equality (i.e. has a Nash equilibrium). We find that this exact structure is exhibited by an interesting robust reinforcement learning problem under an adversarial reward attack, and the validity of its minimax equality immediately follows. This is the first time such a result is established in the literature.
Convergence and Price of Anarchy Guarantees of the Softmax Policy Gradient in Markov Potential Games
Jun 15, 2022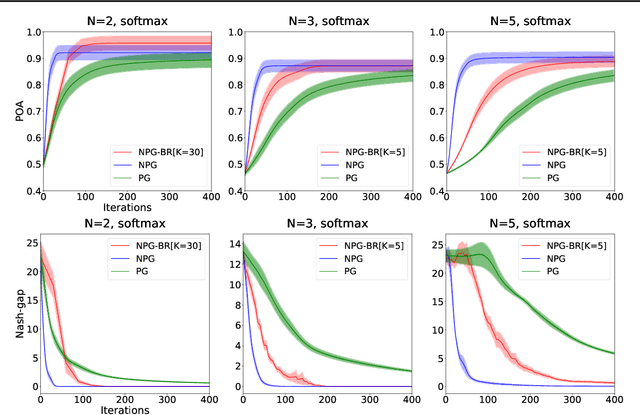

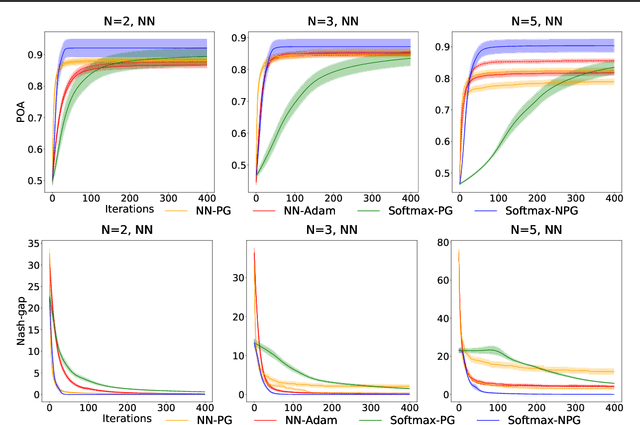
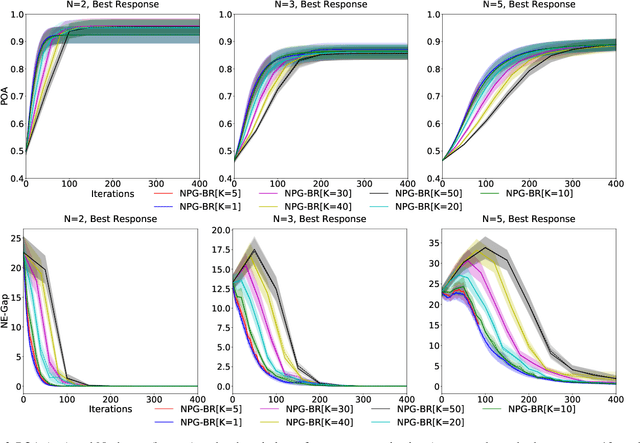
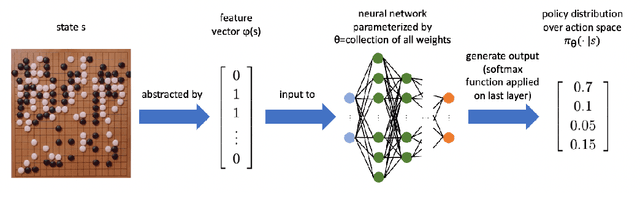
Abstract:We study the performance of policy gradient methods for the subclass of Markov games known as Markov potential games (MPGs), which extends the notion of normal-form potential games to the stateful setting and includes the important special case of the fully cooperative setting where the agents share an identical reward function. Our focus in this paper is to study the convergence of the policy gradient method for solving MPGs under softmax policy parameterization, both tabular and parameterized with general function approximators such as neural networks. We first show the asymptotic convergence of this method to a Nash equilibrium of MPGs for tabular softmax policies. Second, we derive the finite-time performance of the policy gradient in two settings: 1) using the log-barrier regularization, and 2) using the natural policy gradient under the best-response dynamics (NPG-BR). Finally, extending the notion of price of anarchy (POA) and smoothness in normal-form games, we introduce the POA for MPGs and provide a POA bound for NPG-BR. To our knowledge, this is the first POA bound for solving MPGs. To support our theoretical results, we empirically compare the convergence rates and POA of policy gradient variants for both tabular and neural softmax policies.
Regularized Gradient Descent Ascent for Two-Player Zero-Sum Markov Games
May 27, 2022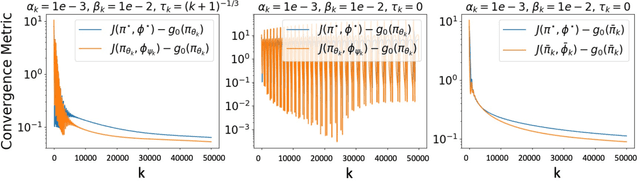
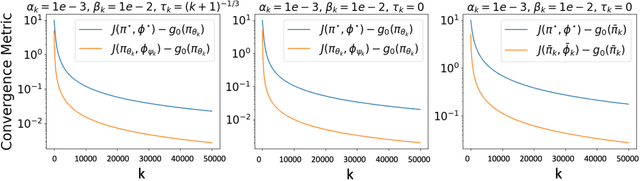
Abstract:We study the problem of finding the Nash equilibrium in a two-player zero-sum Markov game. Due to its formulation as a minimax optimization program, a natural approach to solve the problem is to perform gradient descent/ascent with respect to each player in an alternating fashion. However, due to the non-convexity/non-concavity of the underlying objective function, theoretical understandings of this method are limited. In our paper, we consider solving an entropy-regularized variant of the Markov game. The regularization introduces structure into the optimization landscape that make the solutions more identifiable and allow the problem to be solved more efficiently. Our main contribution is to show that under proper choices of the regularization parameter, the gradient descent ascent algorithm converges to the Nash equilibrium of the original unregularized problem. We explicitly characterize the finite-time performance of the last iterate of our algorithm, which vastly improves over the existing convergence bound of the gradient descent ascent algorithm without regularization. Finally, we complement the analysis with numerical simulations that illustrate the accelerated convergence of the algorithm.
Convergence Rates of Two-Time-Scale Gradient Descent-Ascent Dynamics for Solving Nonconvex Min-Max Problems
Dec 17, 2021
Abstract:There are much recent interests in solving noncovnex min-max optimization problems due to its broad applications in many areas including machine learning, networked resource allocations, and distributed optimization. Perhaps, the most popular first-order method in solving min-max optimization is the so-called simultaneous (or single-loop) gradient descent-ascent algorithm due to its simplicity in implementation. However, theoretical guarantees on the convergence of this algorithm is very sparse since it can diverge even in a simple bilinear problem. In this paper, our focus is to characterize the finite-time performance (or convergence rates) of the continuous-time variant of simultaneous gradient descent-ascent algorithm. In particular, we derive the rates of convergence of this method under a number of different conditions on the underlying objective function, namely, two-sided Polyak-L ojasiewicz (PL), one-sided PL, nonconvex-strongly concave, and strongly convex-nonconcave conditions. Our convergence results improve the ones in prior works under the same conditions of objective functions. The key idea in our analysis is to use the classic singular perturbation theory and coupling Lyapunov functions to address the time-scale difference and interactions between the gradient descent and ascent dynamics. Our results on the behavior of continuous-time algorithm may be used to enhance the convergence properties of its discrete-time counterpart.
Finite-Time Complexity of Online Primal-Dual Natural Actor-Critic Algorithm for Constrained Markov Decision Processes
Oct 21, 2021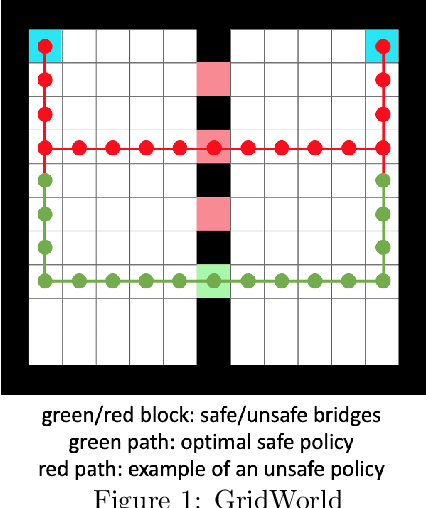
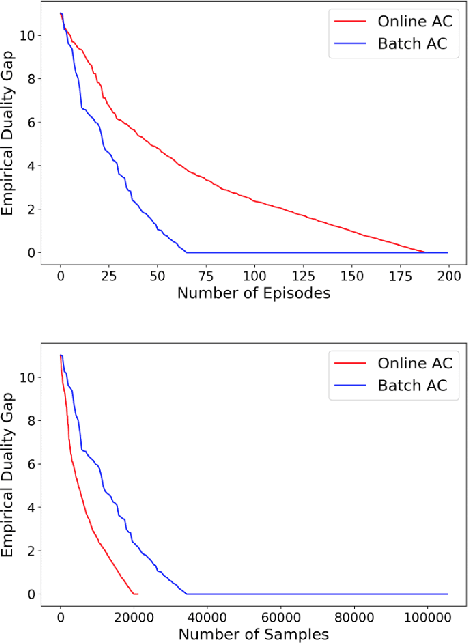
Abstract:We consider a discounted cost constrained Markov decision process (CMDP) policy optimization problem, in which an agent seeks to maximize a discounted cumulative reward subject to a number of constraints on discounted cumulative utilities. To solve this constrained optimization program, we study an online actor-critic variant of a classic primal-dual method where the gradients of both the primal and dual functions are estimated using samples from a single trajectory generated by the underlying time-varying Markov processes. This online primal-dual natural actor-critic algorithm maintains and iteratively updates three variables: a dual variable (or Lagrangian multiplier), a primal variable (or actor), and a critic variable used to estimate the gradients of both primal and dual variables. These variables are updated simultaneously but on different time scales (using different step sizes) and they are all intertwined with each other. Our main contribution is to derive a finite-time analysis for the convergence of this algorithm to the global optimum of a CMDP problem. Specifically, we show that with a proper choice of step sizes the optimality gap and constraint violation converge to zero in expectation at a rate $\mathcal{O}(1/K^{1/6})$, where K is the number of iterations. To our knowledge, this paper is the first to study the finite-time complexity of an online primal-dual actor-critic method for solving a CMDP problem. We also validate the effectiveness of this algorithm through numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge