Accelerating Multi-Task Temporal Difference Learning under Low-Rank Representation

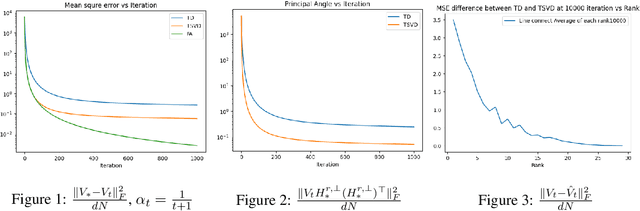
We study policy evaluation problems in multi-task reinforcement learning (RL) under a low-rank representation setting. In this setting, we are given $N$ learning tasks where the corresponding value function of these tasks lie in an $r$-dimensional subspace, with $r<N$. One can apply the classic temporal-difference (TD) learning method for solving these problems where this method learns the value function of each task independently. In this paper, we are interested in understanding whether one can exploit the low-rank structure of the multi-task setting to accelerate the performance of TD learning. To answer this question, we propose a new variant of TD learning method, where we integrate the so-called truncated singular value decomposition step into the update of TD learning. This additional step will enable TD learning to exploit the dominant directions due to the low rank structure to update the iterates, therefore, improving its performance. Our empirical results show that the proposed method significantly outperforms the classic TD learning, where the performance gap increases as the rank $r$ decreases. From the theoretical point of view, introducing the truncated singular value decomposition step into TD learning might cause an instability on the updates. We provide a theoretical result showing that the instability does not happen. Specifically, we prove that the proposed method converges at a rate $\mathcal{O}(\frac{\ln(t)}{t})$, where $t$ is the number of iterations. This rate matches that of the standard TD learning.

External Large Foundation Model: How to Efficiently Serve Trillions of Parameters for Online Ads Recommendation

Ads recommendation is a prominent service of online advertising systems and has been actively studied. Recent studies indicate that scaling-up and advanced design of the recommendation model can bring significant performance improvement. However, with a larger model scale, such prior studies have a significantly increasing gap from industry as they often neglect two fundamental challenges in industrial-scale applications. First, training and inference budgets are restricted for the model to be served, exceeding which may incur latency and impair user experience. Second, large-volume data arrive in a streaming mode with data distributions dynamically shifting, as new users/ads join and existing users/ads leave the system. We propose the External Large Foundation Model (ExFM) framework to address the overlooked challenges. Specifically, we develop external distillation and a data augmentation system (DAS) to control the computational cost of training/inference while maintaining high performance. We design the teacher in a way like a foundation model (FM) that can serve multiple students as vertical models (VMs) to amortize its building cost. We propose Auxiliary Head and Student Adapter to mitigate the data distribution gap between FM and VMs caused by the streaming data issue. Comprehensive experiments on internal industrial-scale applications and public datasets demonstrate significant performance gain by ExFM.

ADAGE: A generic two-layer framework for adaptive agent based modelling

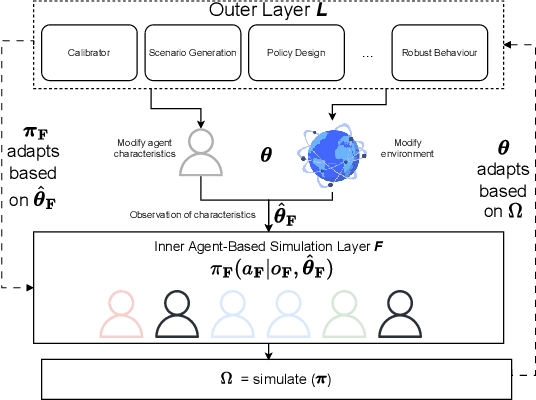
Agent-based models (ABMs) are valuable for modelling complex, potentially out-of-equilibria scenarios. However, ABMs have long suffered from the Lucas critique, stating that agent behaviour should adapt to environmental changes. Furthermore, the environment itself often adapts to these behavioural changes, creating a complex bi-level adaptation problem. Recent progress integrating multi-agent reinforcement learning into ABMs introduces adaptive agent behaviour, beginning to address the first part of this critique, however, the approaches are still relatively ad hoc, lacking a general formulation, and furthermore, do not tackle the second aspect of simultaneously adapting environmental level characteristics in addition to the agent behaviours. In this work, we develop a generic two-layer framework for ADaptive AGEnt based modelling (ADAGE) for addressing these problems. This framework formalises the bi-level problem as a Stackelberg game with conditional behavioural policies, providing a consolidated framework for adaptive agent-based modelling based on solving a coupled set of non-linear equations. We demonstrate how this generic approach encapsulates several common (previously viewed as distinct) ABM tasks, such as policy design, calibration, scenario generation, and robust behavioural learning under one unified framework. We provide example simulations on multiple complex economic and financial environments, showing the strength of the novel framework under these canonical settings, addressing long-standing critiques of traditional ABMs.

Regularized Proportional Fairness Mechanism for Resource Allocation Without Money

Mechanism design in resource allocation studies dividing limited resources among self-interested agents whose satisfaction with the allocation depends on privately held utilities. We consider the problem in a payment-free setting, with the aim of maximizing social welfare while enforcing incentive compatibility (IC), i.e., agents cannot inflate allocations by misreporting their utilities. The well-known proportional fairness (PF) mechanism achieves the maximum possible social welfare but incurs an undesirably high exploitability (the maximum unilateral inflation in utility from misreport and a measure of deviation from IC). In fact, it is known that no mechanism can achieve the maximum social welfare and exact incentive compatibility (IC) simultaneously without the use of monetary incentives (Cole et al., 2013). Motivated by this fact, we propose learning an approximate mechanism that desirably trades off the competing objectives. Our main contribution is to design an innovative neural network architecture tailored to the resource allocation problem, which we name Regularized Proportional Fairness Network (RPF-Net). RPF-Net regularizes the output of the PF mechanism by a learned function approximator of the most exploitable allocation, with the aim of reducing the incentive for any agent to misreport. We derive generalization bounds that guarantee the mechanism performance when trained under finite and out-of-distribution samples and experimentally demonstrate the merits of the proposed mechanism compared to the state-of-the-art.

Approximate Equivariance in Reinforcement Learning

Equivariant neural networks have shown great success in reinforcement learning, improving sample efficiency and generalization when there is symmetry in the task. However, in many problems, only approximate symmetry is present, which makes imposing exact symmetry inappropriate. Recently, approximately equivariant networks have been proposed for supervised classification and modeling physical systems. In this work, we develop approximately equivariant algorithms in reinforcement learning (RL). We define approximately equivariant MDPs and theoretically characterize the effect of approximate equivariance on the optimal Q function. We propose novel RL architectures using relaxed group convolutions and experiment on several continuous control domains and stock trading with real financial data. Our results demonstrate that approximate equivariance matches prior work when exact symmetries are present, and outperforms them when domains exhibit approximate symmetry. As an added byproduct of these techniques, we observe increased robustness to noise at test time.

Partially Observable Contextual Bandits with Linear Payoffs

The standard contextual bandit framework assumes fully observable and actionable contexts. In this work, we consider a new bandit setting with partially observable, correlated contexts and linear payoffs, motivated by the applications in finance where decision making is based on market information that typically displays temporal correlation and is not fully observed. We make the following contributions marrying ideas from statistical signal processing with bandits: (i) We propose an algorithmic pipeline named EMKF-Bandit, which integrates system identification, filtering, and classic contextual bandit algorithms into an iterative method alternating between latent parameter estimation and decision making. (ii) We analyze EMKF-Bandit when we select Thompson sampling as the bandit algorithm and show that it incurs a sub-linear regret under conditions on filtering. (iii) We conduct numerical simulations that demonstrate the benefits and practical applicability of the proposed pipeline.

Fast Two-Time-Scale Stochastic Gradient Method with Applications in Reinforcement Learning

Two-time-scale optimization is a framework introduced in Zeng et al. (2024) that abstracts a range of policy evaluation and policy optimization problems in reinforcement learning (RL). Akin to bi-level optimization under a particular type of stochastic oracle, the two-time-scale optimization framework has an upper level objective whose gradient evaluation depends on the solution of a lower level problem, which is to find the root of a strongly monotone operator. In this work, we propose a new method for solving two-time-scale optimization that achieves significantly faster convergence than the prior arts. The key idea of our approach is to leverage an averaging step to improve the estimates of the operators in both lower and upper levels before using them to update the decision variables. These additional averaging steps eliminate the direct coupling between the main variables, enabling the accelerated performance of our algorithm. We characterize the finite-time convergence rates of the proposed algorithm under various conditions of the underlying objective function, including strong convexity, convexity, Polyak-Lojasiewicz condition, and general non-convexity. These rates significantly improve over the best-known complexity of the standard two-time-scale stochastic approximation algorithm. When applied to RL, we show how the proposed algorithm specializes to novel online sample-based methods that surpass or match the performance of the existing state of the art. Finally, we support our theoretical results with numerical simulations in RL.

Natural Policy Gradient and Actor Critic Methods for Constrained Multi-Task Reinforcement Learning

Multi-task reinforcement learning (RL) aims to find a single policy that effectively solves multiple tasks at the same time. This paper presents a constrained formulation for multi-task RL where the goal is to maximize the average performance of the policy across tasks subject to bounds on the performance in each task. We consider solving this problem both in the centralized setting, where information for all tasks is accessible to a single server, and in the decentralized setting, where a network of agents, each given one task and observing local information, cooperate to find the solution of the globally constrained objective using local communication. We first propose a primal-dual algorithm that provably converges to the globally optimal solution of this constrained formulation under exact gradient evaluations. When the gradient is unknown, we further develop a sampled-based actor-critic algorithm that finds the optimal policy using online samples of state, action, and reward. Finally, we study the extension of the algorithm to the linear function approximation setting.

QCQP-Net: Reliably Learning Feasible Alternating Current Optimal Power Flow Solutions Under Constraints

At the heart of power system operations, alternating current optimal power flow (ACOPF) studies the generation of electric power in the most economical way under network-wide load requirement, and can be formulated as a highly structured non-convex quadratically constrained quadratic program (QCQP). Optimization-based solutions to ACOPF (such as ADMM or interior-point method), as the classic approach, require large amount of computation and cannot meet the need to repeatedly solve the problem as load requirement frequently changes. On the other hand, learning-based methods that directly predict the ACOPF solution given the load input incur little computational cost but often generates infeasible solutions (i.e. violate the constraints of ACOPF). In this work, we combine the best of both worlds -- we propose an innovated framework for learning ACOPF, where the input load is mapped to the ACOPF solution through a neural network in a computationally efficient and reliable manner. Key to our innovation is a specific-purpose "activation function" defined implicitly by a QCQP and a novel loss, which enforce constraint satisfaction. We show through numerical simulations that our proposed method achieves superior feasibility rate and generation cost in situations where the existing learning-based approaches fail.

Near-Optimal Fair Resource Allocation for Strategic Agents without Money: A Data-Driven Approach

We study learning-based design of fair allocation mechanisms for divisible resources, using proportional fairness (PF) as a benchmark. The learning setting is a significant departure from the classic mechanism design literature, in that, we need to learn fair mechanisms solely from data. In particular, we consider the challenging problem of learning one-shot allocation mechanisms -- without the use of money -- that incentivize strategic agents to be truthful when reporting their valuations. It is well-known that the mechanism that directly seeks to optimize PF is not incentive compatible, meaning that the agents can potentially misreport their preferences to gain increased allocations. We introduce the notion of "exploitability" of a mechanism to measure the relative gain in utility from misreport, and make the following important contributions in the paper: (i) Using sophisticated techniques inspired by differentiable convex programming literature, we design a numerically efficient approach for computing the exploitability of the PF mechanism. This novel contribution enables us to quantify the gap that needs to be bridged to approximate PF via incentive compatible mechanisms. (ii) Next, we modify the PF mechanism to introduce a trade-off between fairness and exploitability. By properly controlling this trade-off using data, we show that our proposed mechanism, ExPF-Net, provides a strong approximation to the PF mechanism while maintaining low exploitability. This mechanism, however, comes with a high computational cost. (iii) To address the computational challenges, we propose another mechanism ExS-Net, which is end-to-end parameterized by a neural network. ExS-Net enjoys similar (slightly inferior) performance and significantly accelerated training and inference time performance. (iv) Extensive numerical simulations demonstrate the robustness and efficacy of the proposed mechanisms.