EPO: Diverse and Realistic Protein Ensemble Generation via Energy Preference Optimization

Accurate exploration of protein conformational ensembles is essential for uncovering function but remains hard because molecular-dynamics (MD) simulations suffer from high computational costs and energy-barrier trapping. This paper presents Energy Preference Optimization (EPO), an online refinement algorithm that turns a pretrained protein ensemble generator into an energy-aware sampler without extra MD trajectories. Specifically, EPO leverages stochastic differential equation sampling to explore the conformational landscape and incorporates a novel energy-ranking mechanism based on list-wise preference optimization. Crucially, EPO introduces a practical upper bound to efficiently approximate the intractable probability of long sampling trajectories in continuous-time generative models, making it easily adaptable to existing pretrained generators. On Tetrapeptides, ATLAS, and Fast-Folding benchmarks, EPO successfully generates diverse and physically realistic ensembles, establishing a new state-of-the-art in nine evaluation metrics. These results demonstrate that energy-only preference signals can efficiently steer generative models toward thermodynamically consistent conformational ensembles, providing an alternative to long MD simulations and widening the applicability of learned potentials in structural biology and drug discovery.

Physical Consistency Bridges Heterogeneous Data in Molecular Multi-Task Learning

In recent years, machine learning has demonstrated impressive capability in handling molecular science tasks. To support various molecular properties at scale, machine learning models are trained in the multi-task learning paradigm. Nevertheless, data of different molecular properties are often not aligned: some quantities, e.g. equilibrium structure, demand more cost to compute than others, e.g. energy, so their data are often generated by cheaper computational methods at the cost of lower accuracy, which cannot be directly overcome through multi-task learning. Moreover, it is not straightforward to leverage abundant data of other tasks to benefit a particular task. To handle such data heterogeneity challenges, we exploit the specialty of molecular tasks that there are physical laws connecting them, and design consistency training approaches that allow different tasks to exchange information directly so as to improve one another. Particularly, we demonstrate that the more accurate energy data can improve the accuracy of structure prediction. We also find that consistency training can directly leverage force and off-equilibrium structure data to improve structure prediction, demonstrating a broad capability for integrating heterogeneous data.

Neural P$^3$M: A Long-Range Interaction Modeling Enhancer for Geometric GNNs

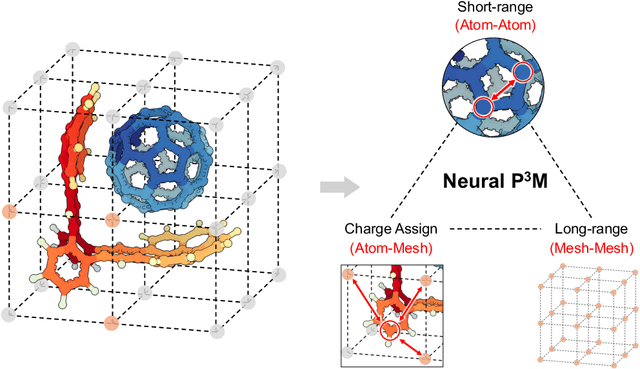
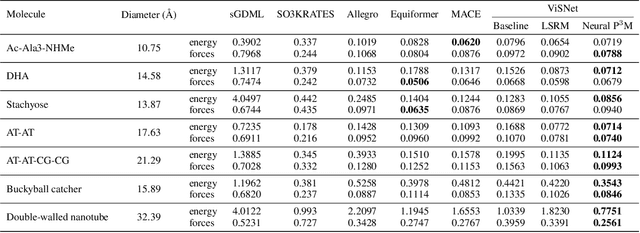
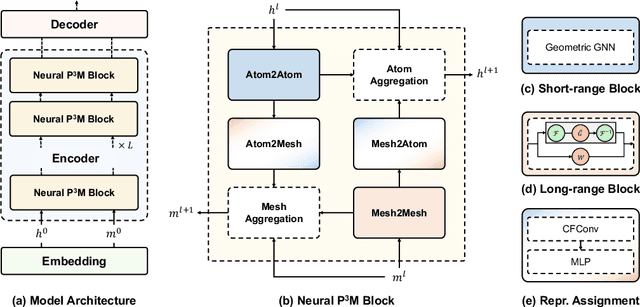
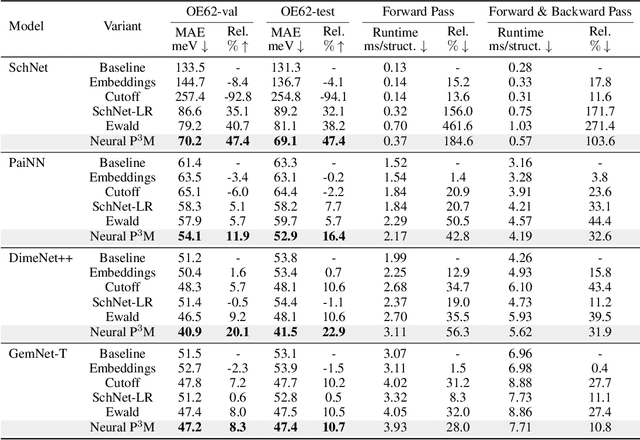
Geometric graph neural networks (GNNs) have emerged as powerful tools for modeling molecular geometry. However, they encounter limitations in effectively capturing long-range interactions in large molecular systems. To address this challenge, we introduce Neural P$^3$M, a versatile enhancer of geometric GNNs to expand the scope of their capabilities by incorporating mesh points alongside atoms and reimaging traditional mathematical operations in a trainable manner. Neural P$^3$M exhibits flexibility across a wide range of molecular systems and demonstrates remarkable accuracy in predicting energies and forces, outperforming on benchmarks such as the MD22 dataset. It also achieves an average improvement of 22% on the OE62 dataset while integrating with various architectures.

QCQP-Net: Reliably Learning Feasible Alternating Current Optimal Power Flow Solutions Under Constraints

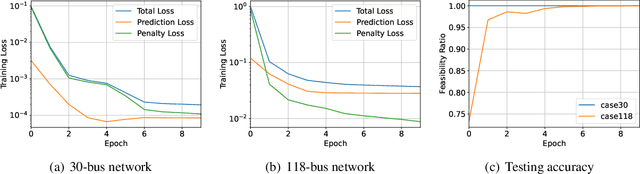
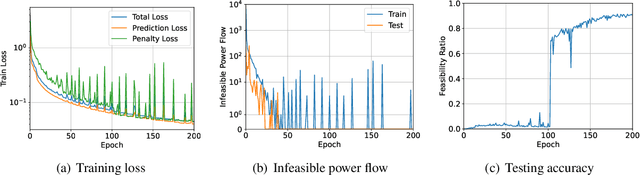
At the heart of power system operations, alternating current optimal power flow (ACOPF) studies the generation of electric power in the most economical way under network-wide load requirement, and can be formulated as a highly structured non-convex quadratically constrained quadratic program (QCQP). Optimization-based solutions to ACOPF (such as ADMM or interior-point method), as the classic approach, require large amount of computation and cannot meet the need to repeatedly solve the problem as load requirement frequently changes. On the other hand, learning-based methods that directly predict the ACOPF solution given the load input incur little computational cost but often generates infeasible solutions (i.e. violate the constraints of ACOPF). In this work, we combine the best of both worlds -- we propose an innovated framework for learning ACOPF, where the input load is mapped to the ACOPF solution through a neural network in a computationally efficient and reliable manner. Key to our innovation is a specific-purpose "activation function" defined implicitly by a QCQP and a novel loss, which enforce constraint satisfaction. We show through numerical simulations that our proposed method achieves superior feasibility rate and generation cost in situations where the existing learning-based approaches fail.