Bridging Geometric States via Geometric Diffusion Bridge

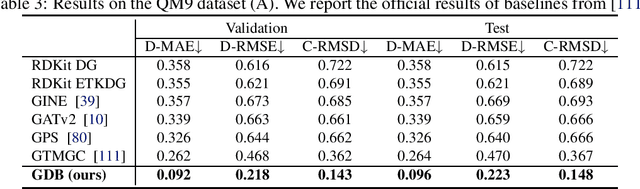
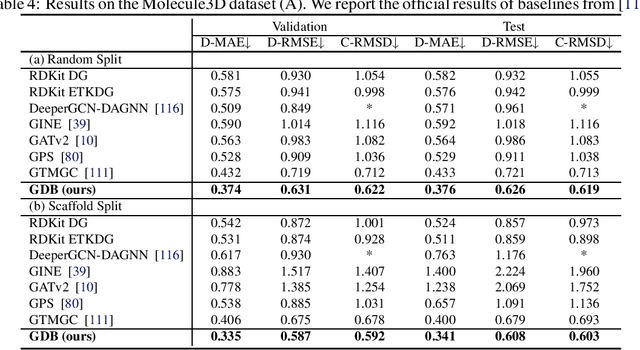
The accurate prediction of geometric state evolution in complex systems is critical for advancing scientific domains such as quantum chemistry and material modeling. Traditional experimental and computational methods face challenges in terms of environmental constraints and computational demands, while current deep learning approaches still fall short in terms of precision and generality. In this work, we introduce the Geometric Diffusion Bridge (GDB), a novel generative modeling framework that accurately bridges initial and target geometric states. GDB leverages a probabilistic approach to evolve geometric state distributions, employing an equivariant diffusion bridge derived by a modified version of Doob's $h$-transform for connecting geometric states. This tailored diffusion process is anchored by initial and target geometric states as fixed endpoints and governed by equivariant transition kernels. Moreover, trajectory data can be seamlessly leveraged in our GDB framework by using a chain of equivariant diffusion bridges, providing a more detailed and accurate characterization of evolution dynamics. Theoretically, we conduct a thorough examination to confirm our framework's ability to preserve joint distributions of geometric states and capability to completely model the underlying dynamics inducing trajectory distributions with negligible error. Experimental evaluations across various real-world scenarios show that GDB surpasses existing state-of-the-art approaches, opening up a new pathway for accurately bridging geometric states and tackling crucial scientific challenges with improved accuracy and applicability.

How Numerical Precision Affects Mathematical Reasoning Capabilities of LLMs

Despite the remarkable success of Transformer-based Large Language Models (LLMs) across various domains, understanding and enhancing their mathematical capabilities remains a significant challenge. In this paper, we conduct a rigorous theoretical analysis of LLMs' mathematical abilities, with a specific focus on their arithmetic performances. We identify numerical precision as a key factor that influences their effectiveness in mathematical tasks. Our results show that Transformers operating with low numerical precision fail to address arithmetic tasks, such as iterated addition and integer multiplication, unless the model size grows super-polynomially with respect to the input length. In contrast, Transformers with standard numerical precision can efficiently handle these tasks with significantly smaller model sizes. We further support our theoretical findings through empirical experiments that explore the impact of varying numerical precision on arithmetic tasks, providing valuable insights for improving the mathematical reasoning capabilities of LLMs.

Physical Consistency Bridges Heterogeneous Data in Molecular Multi-Task Learning

In recent years, machine learning has demonstrated impressive capability in handling molecular science tasks. To support various molecular properties at scale, machine learning models are trained in the multi-task learning paradigm. Nevertheless, data of different molecular properties are often not aligned: some quantities, e.g. equilibrium structure, demand more cost to compute than others, e.g. energy, so their data are often generated by cheaper computational methods at the cost of lower accuracy, which cannot be directly overcome through multi-task learning. Moreover, it is not straightforward to leverage abundant data of other tasks to benefit a particular task. To handle such data heterogeneity challenges, we exploit the specialty of molecular tasks that there are physical laws connecting them, and design consistency training approaches that allow different tasks to exchange information directly so as to improve one another. Particularly, we demonstrate that the more accurate energy data can improve the accuracy of structure prediction. We also find that consistency training can directly leverage force and off-equilibrium structure data to improve structure prediction, demonstrating a broad capability for integrating heterogeneous data.

Let the Code LLM Edit Itself When You Edit the Code

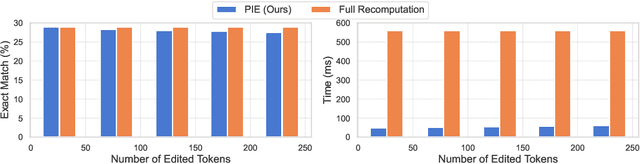
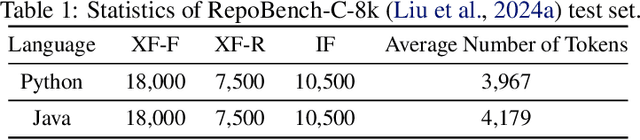
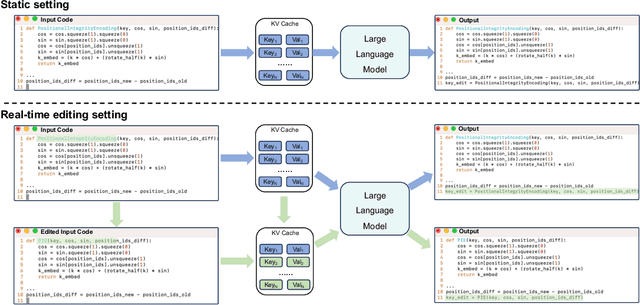
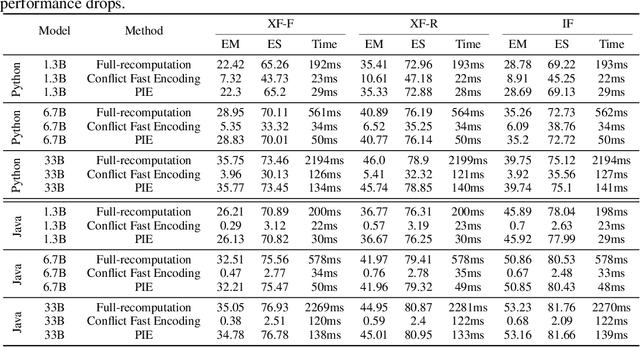
In this work, we investigate a typical scenario in code generation where a developer edits existing code in real time and requests a code assistant, e.g., a large language model, to re-predict the next token or next line on the fly. Naively, the LLM needs to re-encode the entire KV cache to provide an accurate prediction. However, this process is computationally expensive, especially when the sequence length is long. Simply encoding the edited subsequence and integrating it to the original KV cache meets the temporal confusion problem, leading to significantly worse performance. We address this efficiency and accuracy trade-off by introducing \underline{\textbf{Positional \textbf{I}ntegrity \textbf{E}ncoding} (PIE). Building upon the rotary positional encoding, PIE first removes the rotary matrices in the Key cache that introduce temporal confusion and then reapplies the correct rotary matrices. This process ensures that positional relationships between tokens are correct and requires only a single round of matrix multiplication. We validate the effectiveness of PIE through extensive experiments on the RepoBench-C-8k dataset, utilizing DeepSeek-Coder models with 1.3B, 6.7B, and 33B parameters. Our evaluation includes three real-world coding tasks: code insertion, code deletion, and multi-place code editing. Results demonstrate that PIE reduces computational overhead by over 85% compared to the standard full recomputation approach across all model sizes and tasks while well approximating the model performance.

GeoMFormer: A General Architecture for Geometric Molecular Representation Learning

Molecular modeling, a central topic in quantum mechanics, aims to accurately calculate the properties and simulate the behaviors of molecular systems. The molecular model is governed by physical laws, which impose geometric constraints such as invariance and equivariance to coordinate rotation and translation. While numerous deep learning approaches have been developed to learn molecular representations under these constraints, most of them are built upon heuristic and costly modules. We argue that there is a strong need for a general and flexible framework for learning both invariant and equivariant features. In this work, we introduce a novel Transformer-based molecular model called GeoMFormer to achieve this goal. Using the standard Transformer modules, two separate streams are developed to maintain and learn invariant and equivariant representations. Carefully designed cross-attention modules bridge the two streams, allowing information fusion and enhancing geometric modeling in each stream. As a general and flexible architecture, we show that many previous architectures can be viewed as special instantiations of GeoMFormer. Extensive experiments are conducted to demonstrate the power of GeoMFormer. All empirical results show that GeoMFormer achieves strong performance on both invariant and equivariant tasks of different types and scales. Code and models will be made publicly available at https://github.com/c-tl/GeoMFormer.

Two Stones Hit One Bird: Bilevel Positional Encoding for Better Length Extrapolation

In this work, we leverage the intrinsic segmentation of language sequences and design a new positional encoding method called Bilevel Positional Encoding (BiPE). For each position, our BiPE blends an intra-segment encoding and an inter-segment encoding. The intra-segment encoding identifies the locations within a segment and helps the model capture the semantic information therein via absolute positional encoding. The inter-segment encoding specifies the segment index, models the relationships between segments, and aims to improve extrapolation capabilities via relative positional encoding. Theoretical analysis shows this disentanglement of positional information makes learning more effective. The empirical results also show that our BiPE has superior length extrapolation capabilities across a wide range of tasks in diverse text modalities.

Enabling Efficient Equivariant Operations in the Fourier Basis via Gaunt Tensor Products

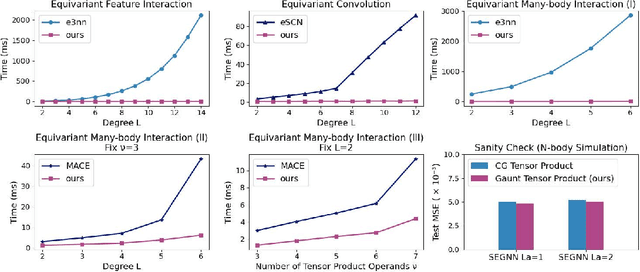
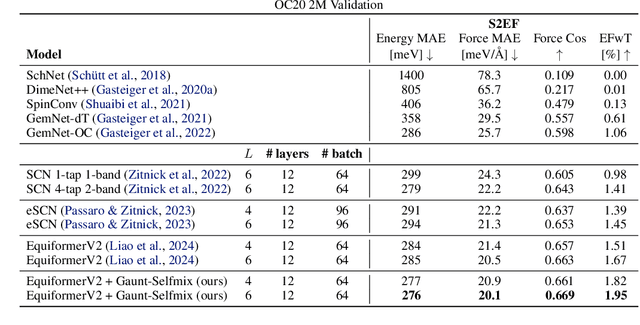
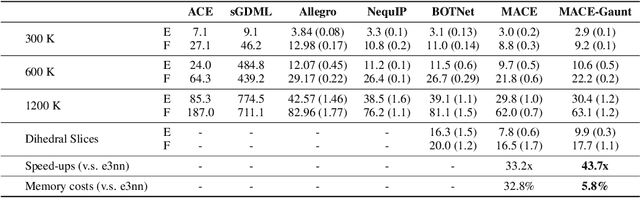
Developing equivariant neural networks for the E(3) group plays an important role in modeling 3D data across real-world applications. Enforcing this equivariance primarily involves the tensor products of irreducible representations (irreps). However, the computational complexity of such operations increases significantly as higher-order tensors are used. In this work, we propose a systematic approach to substantially accelerate the computation of the tensor products of irreps. We mathematically connect the commonly used Clebsch-Gordan coefficients to the Gaunt coefficients, which are integrals of products of three spherical harmonics. Through Gaunt coefficients, the tensor product of irreps becomes equivalent to the multiplication between spherical functions represented by spherical harmonics. This perspective further allows us to change the basis for the equivariant operations from spherical harmonics to a 2D Fourier basis. Consequently, the multiplication between spherical functions represented by a 2D Fourier basis can be efficiently computed via the convolution theorem and Fast Fourier Transforms. This transformation reduces the complexity of full tensor products of irreps from $\mathcal{O}(L^6)$ to $\mathcal{O}(L^3)$, where $L$ is the max degree of irreps. Leveraging this approach, we introduce the Gaunt Tensor Product, which serves as a new method to construct efficient equivariant operations across different model architectures. Our experiments on the Open Catalyst Project and 3BPA datasets demonstrate both the increased efficiency and improved performance of our approach.

Learning a Fourier Transform for Linear Relative Positional Encodings in Transformers

We propose a new class of linear Transformers called FourierLearner-Transformers (FLTs), which incorporate a wide range of relative positional encoding mechanisms (RPEs). These include regular RPE techniques applied for nongeometric data, as well as novel RPEs operating on the sequences of tokens embedded in higher-dimensional Euclidean spaces (e.g. point clouds). FLTs construct the optimal RPE mechanism implicitly by learning its spectral representation. As opposed to other architectures combining efficient low-rank linear attention with RPEs, FLTs remain practical in terms of their memory usage and do not require additional assumptions about the structure of the RPE-mask. FLTs allow also for applying certain structural inductive bias techniques to specify masking strategies, e.g. they provide a way to learn the so-called local RPEs introduced in this paper and providing accuracy gains as compared with several other linear Transformers for language modeling. We also thoroughly tested FLTs on other data modalities and tasks, such as: image classification and 3D molecular modeling. For 3D-data FLTs are, to the best of our knowledge, the first Transformers architectures providing RPE-enhanced linear attention.

Rethinking the Expressive Power of GNNs via Graph Biconnectivity

Designing expressive Graph Neural Networks (GNNs) is a central topic in learning graph-structured data. While numerous approaches have been proposed to improve GNNs in terms of the Weisfeiler-Lehman (WL) test, generally there is still a lack of deep understanding of what additional power they can systematically and provably gain. In this paper, we take a fundamentally different perspective to study the expressive power of GNNs beyond the WL test. Specifically, we introduce a novel class of expressivity metrics via graph biconnectivity and highlight their importance in both theory and practice. As biconnectivity can be easily calculated using simple algorithms that have linear computational costs, it is natural to expect that popular GNNs can learn it easily as well. However, after a thorough review of prior GNN architectures, we surprisingly find that most of them are not expressive for any of these metrics. The only exception is the ESAN framework (Bevilacqua et al., 2022), for which we give a theoretical justification of its power. We proceed to introduce a principled and more efficient approach, called the Generalized Distance Weisfeiler-Lehman (GD-WL), which is provably expressive for all biconnectivity metrics. Practically, we show GD-WL can be implemented by a Transformer-like architecture that preserves expressiveness and enjoys full parallelizability. A set of experiments on both synthetic and real datasets demonstrates that our approach can consistently outperform prior GNN architectures.

One Transformer Can Understand Both 2D & 3D Molecular Data

Unlike vision and language data which usually has a unique format, molecules can naturally be characterized using different chemical formulations. One can view a molecule as a 2D graph or define it as a collection of atoms located in a 3D space. For molecular representation learning, most previous works designed neural networks only for a particular data format, making the learned models likely to fail for other data formats. We believe a general-purpose neural network model for chemistry should be able to handle molecular tasks across data modalities. To achieve this goal, in this work, we develop a novel Transformer-based Molecular model called Transformer-M, which can take molecular data of 2D or 3D formats as input and generate meaningful semantic representations. Using the standard Transformer as the backbone architecture, Transformer-M develops two separated channels to encode 2D and 3D structural information and incorporate them with the atom features in the network modules. When the input data is in a particular format, the corresponding channel will be activated, and the other will be disabled. By training on 2D and 3D molecular data with properly designed supervised signals, Transformer-M automatically learns to leverage knowledge from different data modalities and correctly capture the representations. We conducted extensive experiments for Transformer-M. All empirical results show that Transformer-M can simultaneously achieve strong performance on 2D and 3D tasks, suggesting its broad applicability. The code and models will be made publicly available at https://github.com/lsj2408/Transformer-M.