ViewMask-1-to-3: Multi-View Consistent Image Generation via Multimodal Diffusion Models

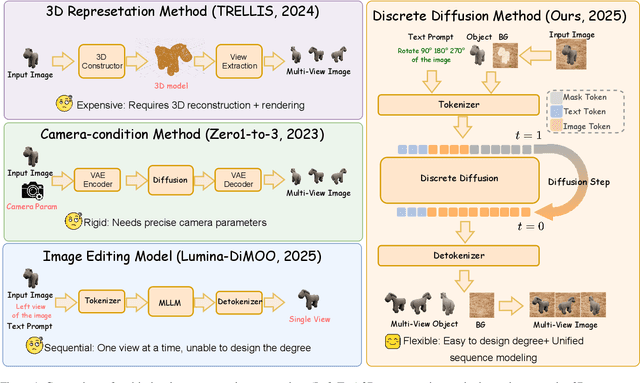
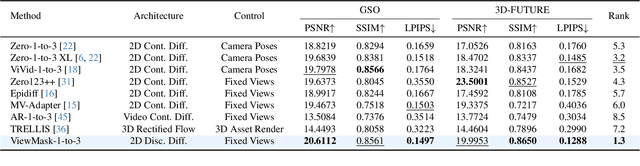
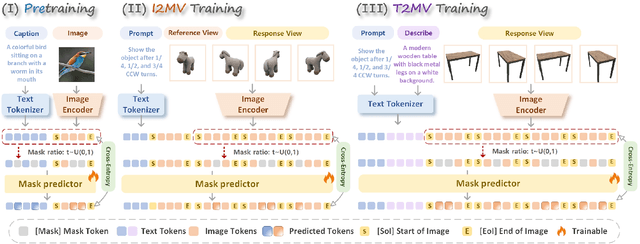
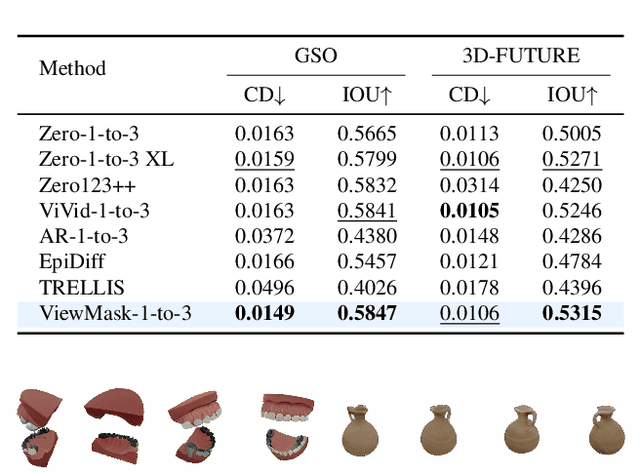
Multi-view image generation from a single image and text description remains challenging due to the difficulty of maintaining geometric consistency across different viewpoints. Existing approaches typically rely on 3D-aware architectures or specialized diffusion models that require extensive multi-view training data and complex geometric priors. In this work, we introduce ViewMask-1-to-3, a pioneering approach to apply discrete diffusion models to multi-view image generation. Unlike continuous diffusion methods that operate in latent spaces, ViewMask-1-to-3 formulates multi-view synthesis as a discrete sequence modeling problem, where each viewpoint is represented as visual tokens obtained through MAGVIT-v2 tokenization. By unifying language and vision through masked token prediction, our approach enables progressive generation of multiple viewpoints through iterative token unmasking with text input. ViewMask-1-to-3 achieves cross-view consistency through simple random masking combined with self-attention, eliminating the requirement for complex 3D geometric constraints or specialized attention architectures. Our approach demonstrates that discrete diffusion provides a viable and simple alternative to existing multi-view generation methods, ranking first on average across GSO and 3D-FUTURE datasets in terms of PSNR, SSIM, and LPIPS, while maintaining architectural simplicity.

Masked Diffusion Models as Energy Minimization

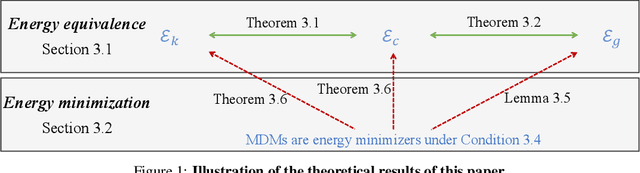
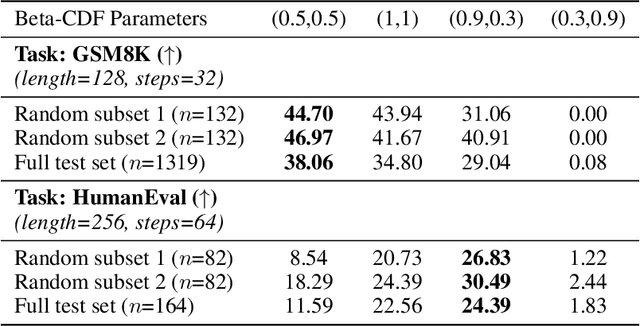
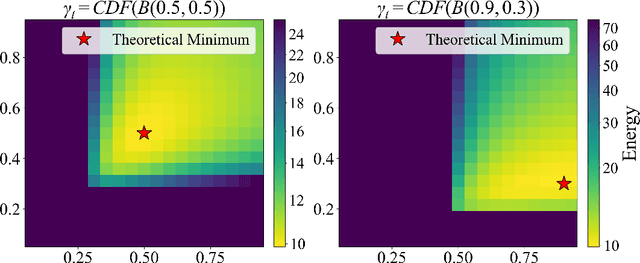
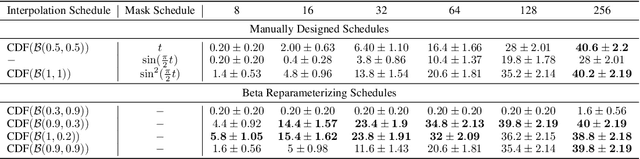
We present a systematic theoretical framework that interprets masked diffusion models (MDMs) as solutions to energy minimization problems in discrete optimal transport. Specifically, we prove that three distinct energy formulations--kinetic, conditional kinetic, and geodesic energy--are mathematically equivalent under the structure of MDMs, and that MDMs minimize all three when the mask schedule satisfies a closed-form optimality condition. This unification not only clarifies the theoretical foundations of MDMs, but also motivates practical improvements in sampling. By parameterizing interpolation schedules via Beta distributions, we reduce the schedule design space to a tractable 2D search, enabling efficient post-training tuning without model modification. Experiments on synthetic and real-world benchmarks demonstrate that our energy-inspired schedules outperform hand-crafted baselines, particularly in low-step sampling settings.

Mathesis: Towards Formal Theorem Proving from Natural Languages

Recent advances in large language models show strong promise for formal reasoning. However, most LLM-based theorem provers have long been constrained by the need for expert-written formal statements as inputs, limiting their applicability to real-world problems expressed in natural language. We tackle this gap with Mathesis, the first end-to-end theorem proving pipeline processing informal problem statements. It contributes Mathesis-Autoformalizer, the first autoformalizer using reinforcement learning to enhance the formalization ability of natural language problems, aided by our novel LeanScorer framework for nuanced formalization quality assessment. It also proposes a Mathesis-Prover, which generates formal proofs from the formalized statements. To evaluate the real-world applicability of end-to-end formal theorem proving, we introduce Gaokao-Formal, a benchmark of 488 complex problems from China's national college entrance exam. Our approach is carefully designed, with a thorough study of each component. Experiments demonstrate Mathesis's effectiveness, with the autoformalizer outperforming the best baseline by 22% in pass-rate on Gaokao-Formal. The full system surpasses other model combinations, achieving 64% accuracy on MiniF2F with pass@32 and a state-of-the-art 18% on Gaokao-Formal.

FUDOKI: Discrete Flow-based Unified Understanding and Generation via Kinetic-Optimal Velocities

The rapid progress of large language models (LLMs) has catalyzed the emergence of multimodal large language models (MLLMs) that unify visual understanding and image generation within a single framework. However, most existing MLLMs rely on autoregressive (AR) architectures, which impose inherent limitations on future development, such as the raster-scan order in image generation and restricted reasoning abilities in causal context modeling. In this work, we challenge the dominance of AR-based approaches by introducing FUDOKI, a unified multimodal model purely based on discrete flow matching, as an alternative to conventional AR paradigms. By leveraging metric-induced probability paths with kinetic optimal velocities, our framework goes beyond the previous masking-based corruption process, enabling iterative refinement with self-correction capability and richer bidirectional context integration during generation. To mitigate the high cost of training from scratch, we initialize FUDOKI from pre-trained AR-based MLLMs and adaptively transition to the discrete flow matching paradigm. Experimental results show that FUDOKI achieves performance comparable to state-of-the-art AR-based MLLMs across both visual understanding and image generation tasks, highlighting its potential as a foundation for next-generation unified multimodal models. Furthermore, we show that applying test-time scaling techniques to FUDOKI yields significant performance gains, further underscoring its promise for future enhancement through reinforcement learning.

Variational Autoencoding Discrete Diffusion with Enhanced Dimensional Correlations Modeling

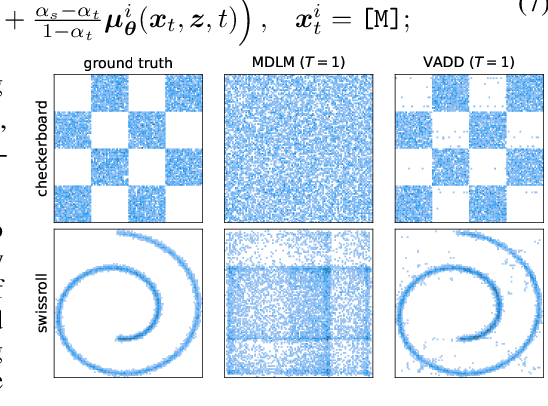
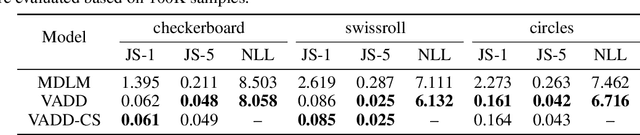
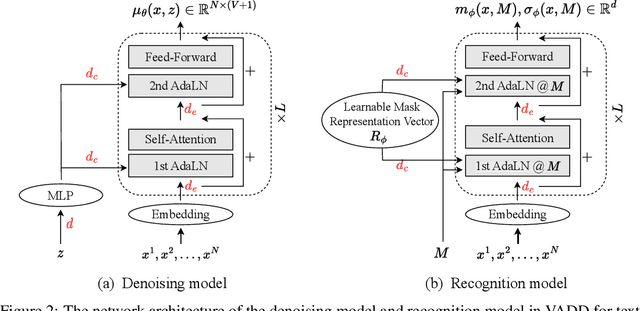
Discrete diffusion models have recently shown great promise for modeling complex discrete data, with masked diffusion models (MDMs) offering a compelling trade-off between quality and generation speed. MDMs denoise by progressively unmasking multiple dimensions from an all-masked input, but their performance can degrade when using few denoising steps due to limited modeling of inter-dimensional dependencies. In this paper, we propose Variational Autoencoding Discrete Diffusion (VADD), a novel framework that enhances discrete diffusion with latent variable modeling to implicitly capture correlations among dimensions. By introducing an auxiliary recognition model, VADD enables stable training via variational lower bounds maximization and amortized inference over the training set. Our approach retains the efficiency of traditional MDMs while significantly improving sample quality, especially when the number of denoising steps is small. Empirical results on 2D toy data, pixel-level image generation, and text generation demonstrate that VADD consistently outperforms MDM baselines.

Learning Few-Step Diffusion Models by Trajectory Distribution Matching

Accelerating diffusion model sampling is crucial for efficient AIGC deployment. While diffusion distillation methods -- based on distribution matching and trajectory matching -- reduce sampling to as few as one step, they fall short on complex tasks like text-to-image generation. Few-step generation offers a better balance between speed and quality, but existing approaches face a persistent trade-off: distribution matching lacks flexibility for multi-step sampling, while trajectory matching often yields suboptimal image quality. To bridge this gap, we propose learning few-step diffusion models by Trajectory Distribution Matching (TDM), a unified distillation paradigm that combines the strengths of distribution and trajectory matching. Our method introduces a data-free score distillation objective, aligning the student's trajectory with the teacher's at the distribution level. Further, we develop a sampling-steps-aware objective that decouples learning targets across different steps, enabling more adjustable sampling. This approach supports both deterministic sampling for superior image quality and flexible multi-step adaptation, achieving state-of-the-art performance with remarkable efficiency. Our model, TDM, outperforms existing methods on various backbones, such as SDXL and PixArt-$\alpha$, delivering superior quality and significantly reduced training costs. In particular, our method distills PixArt-$\alpha$ into a 4-step generator that outperforms its teacher on real user preference at 1024 resolution. This is accomplished with 500 iterations and 2 A800 hours -- a mere 0.01% of the teacher's training cost. In addition, our proposed TDM can be extended to accelerate text-to-video diffusion. Notably, TDM can outperform its teacher model (CogVideoX-2B) by using only 4 NFE on VBench, improving the total score from 80.91 to 81.65. Project page: https://tdm-t2x.github.io/

Adding Additional Control to One-Step Diffusion with Joint Distribution Matching

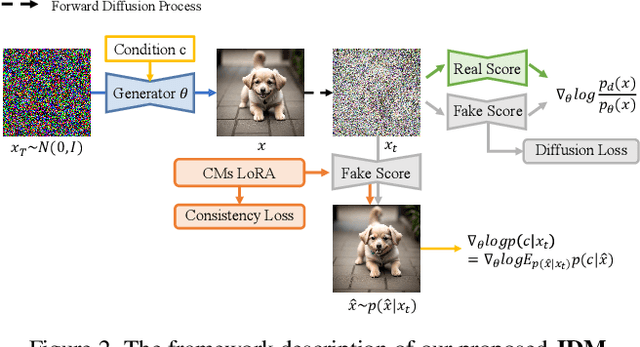
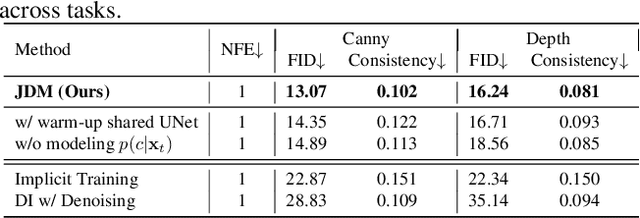
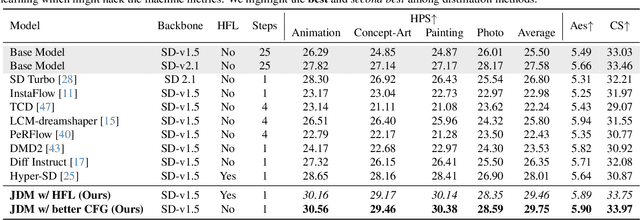
While diffusion distillation has enabled one-step generation through methods like Variational Score Distillation, adapting distilled models to emerging new controls -- such as novel structural constraints or latest user preferences -- remains challenging. Conventional approaches typically requires modifying the base diffusion model and redistilling it -- a process that is both computationally intensive and time-consuming. To address these challenges, we introduce Joint Distribution Matching (JDM), a novel approach that minimizes the reverse KL divergence between image-condition joint distributions. By deriving a tractable upper bound, JDM decouples fidelity learning from condition learning. This asymmetric distillation scheme enables our one-step student to handle controls unknown to the teacher model and facilitates improved classifier-free guidance (CFG) usage and seamless integration of human feedback learning (HFL). Experimental results demonstrate that JDM surpasses baseline methods such as multi-step ControlNet by mere one-step in most cases, while achieving state-of-the-art performance in one-step text-to-image synthesis through improved usage of CFG or HFL integration.

Efficient Neural Theorem Proving via Fine-grained Proof Structure Analysis

The synergy between deep learning models and traditional automation tools plays a pivotal role in developing robust neural theorem provers (NTPs). However, for proof synthesis with LLMs, previous work applies automation tools either only when the model explicitly calls the method, or only at a single granularity level, failing to fully exploit the power of built-in tactics and off-the-shelf automated theorem provers. In this work, we propose ProofAug, a novel theorem proving method that enjoys superior sample efficiency through equipping proof-generation LLMs with automation methods in different granularities via fine-grained structure analysis of model-generated proof proposals. Furthermore, ProofAug serves as a versatile plug-and-play module that seamlessly integrates with any tree-search algorithm, enabling our construction of an efficient recursive proving (ERP) module to further enhance performance. The superiority of our method is validated on the miniF2F-test benchmark using the open-source deepseek-math-7b-base model and the Isabelle proof assistant. Notably, by additionally employing a mixed prompting strategy, we achieve a cumulative pass rate of 66.0% after curation of the dataset (61.9% for the original version), setting a new SOTA across all proof languages with a total sample budget of only 2100. Our code is available at https://github.com/haoxiongliu/ProofAug.

GTA: Global Tracklet Association for Multi-Object Tracking in Sports

Multi-object tracking in sports scenarios has become one of the focal points in computer vision, experiencing significant advancements through the integration of deep learning techniques. Despite these breakthroughs, challenges remain, such as accurately re-identifying players upon re-entry into the scene and minimizing ID switches. In this paper, we propose an appearance-based global tracklet association algorithm designed to enhance tracking performance by splitting tracklets containing multiple identities and connecting tracklets seemingly from the same identity. This method can serve as a plug-and-play refinement tool for any multi-object tracker to further boost their performance. The proposed method achieved a new state-of-the-art performance on the SportsMOT dataset with HOTA score of 81.04%. Similarly, on the SoccerNet dataset, our method enhanced multiple trackers' performance, consistently increasing the HOTA score from 79.41% to 83.11%. These significant and consistent improvements across different trackers and datasets underscore our proposed method's potential impact on the application of sports player tracking. We open-source our project codebase at https://github.com/sjc042/gta-link.git.

How Numerical Precision Affects Mathematical Reasoning Capabilities of LLMs

Despite the remarkable success of Transformer-based Large Language Models (LLMs) across various domains, understanding and enhancing their mathematical capabilities remains a significant challenge. In this paper, we conduct a rigorous theoretical analysis of LLMs' mathematical abilities, with a specific focus on their arithmetic performances. We identify numerical precision as a key factor that influences their effectiveness in mathematical tasks. Our results show that Transformers operating with low numerical precision fail to address arithmetic tasks, such as iterated addition and integer multiplication, unless the model size grows super-polynomially with respect to the input length. In contrast, Transformers with standard numerical precision can efficiently handle these tasks with significantly smaller model sizes. We further support our theoretical findings through empirical experiments that explore the impact of varying numerical precision on arithmetic tasks, providing valuable insights for improving the mathematical reasoning capabilities of LLMs.