Solving the Hubbard model with Neural Quantum States

The rapid development of neural quantum states (NQS) has established it as a promising framework for studying quantum many-body systems. In this work, by leveraging the cutting-edge transformer-based architectures and developing highly efficient optimization algorithms, we achieve the state-of-the-art results for the doped two-dimensional (2D) Hubbard model, arguably the minimum model for high-Tc superconductivity. Interestingly, we find different attention heads in the NQS ansatz can directly encode correlations at different scales, making it capable of capturing long-range correlations and entanglements in strongly correlated systems. With these advances, we establish the half-filled stripe in the ground state of 2D Hubbard model with the next nearest neighboring hoppings, consistent with experimental observations in cuprates. Our work establishes NQS as a powerful tool for solving challenging many-fermions systems.

How Numerical Precision Affects Mathematical Reasoning Capabilities of LLMs

Despite the remarkable success of Transformer-based Large Language Models (LLMs) across various domains, understanding and enhancing their mathematical capabilities remains a significant challenge. In this paper, we conduct a rigorous theoretical analysis of LLMs' mathematical abilities, with a specific focus on their arithmetic performances. We identify numerical precision as a key factor that influences their effectiveness in mathematical tasks. Our results show that Transformers operating with low numerical precision fail to address arithmetic tasks, such as iterated addition and integer multiplication, unless the model size grows super-polynomially with respect to the input length. In contrast, Transformers with standard numerical precision can efficiently handle these tasks with significantly smaller model sizes. We further support our theoretical findings through empirical experiments that explore the impact of varying numerical precision on arithmetic tasks, providing valuable insights for improving the mathematical reasoning capabilities of LLMs.

Towards Differentiable Multilevel Optimization: A Gradient-Based Approach

Multilevel optimization has gained renewed interest in machine learning due to its promise in applications such as hyperparameter tuning and continual learning. However, existing methods struggle with the inherent difficulty of efficiently handling the nested structure. This paper introduces a novel gradient-based approach for multilevel optimization that overcomes these limitations by leveraging a hierarchically structured decomposition of the full gradient and employing advanced propagation techniques. Extending to n-level scenarios, our method significantly reduces computational complexity while improving both solution accuracy and convergence speed. We demonstrate the effectiveness of our approach through numerical experiments, comparing it with existing methods across several benchmarks. The results show a notable improvement in solution accuracy. To the best of our knowledge, this is one of the first algorithms to provide a general version of implicit differentiation with both theoretical guarantees and superior empirical performance.

QCircuitNet: A Large-Scale Hierarchical Dataset for Quantum Algorithm Design

Quantum computing is an emerging field recognized for the significant speedup it offers over classical computing through quantum algorithms. However, designing and implementing quantum algorithms pose challenges due to the complex nature of quantum mechanics and the necessity for precise control over quantum states. Despite the significant advancements in AI, there has been a lack of datasets specifically tailored for this purpose. In this work, we introduce QCircuitNet, the first benchmark and test dataset designed to evaluate AI's capability in designing and implementing quantum algorithms in the form of quantum circuit codes. Unlike using AI for writing traditional codes, this task is fundamentally different and significantly more complicated due to highly flexible design space and intricate manipulation of qubits. Our key contributions include: 1. A general framework which formulates the key features of quantum algorithm design task for Large Language Models. 2. Implementation for a wide range of quantum algorithms from basic primitives to advanced applications, with easy extension to more quantum algorithms. 3. Automatic validation and verification functions, allowing for iterative evaluation and interactive reasoning without human inspection. 4. Promising potential as a training dataset through primitive fine-tuning results. We observed several interesting experimental phenomena: fine-tuning does not always outperform few-shot learning, and LLMs tend to exhibit consistent error patterns. QCircuitNet provides a comprehensive benchmark for AI-driven quantum algorithm design, offering advantages in model evaluation and improvement, while also revealing some limitations of LLMs in this domain.

FLatS: Principled Out-of-Distribution Detection with Feature-Based Likelihood Ratio Score

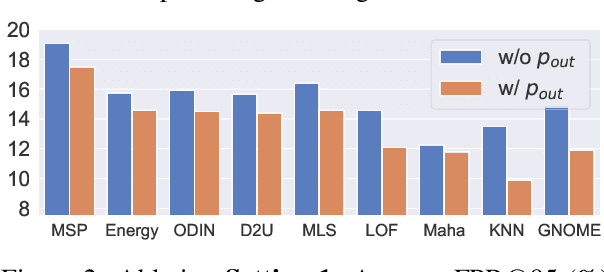
Detecting out-of-distribution (OOD) instances is crucial for NLP models in practical applications. Although numerous OOD detection methods exist, most of them are empirical. Backed by theoretical analysis, this paper advocates for the measurement of the "OOD-ness" of a test case $\boldsymbol{x}$ through the likelihood ratio between out-distribution $\mathcal P_{\textit{out}}$ and in-distribution $\mathcal P_{\textit{in}}$. We argue that the state-of-the-art (SOTA) feature-based OOD detection methods, such as Maha and KNN, are suboptimal since they only estimate in-distribution density $p_{\textit{in}}(\boldsymbol{x})$. To address this issue, we propose FLatS, a principled solution for OOD detection based on likelihood ratio. Moreover, we demonstrate that FLatS can serve as a general framework capable of enhancing other OOD detection methods by incorporating out-distribution density $p_{\textit{out}}(\boldsymbol{x})$ estimation. Experiments show that FLatS establishes a new SOTA on popular benchmarks. Our code is publicly available at https://github.com/linhaowei1/FLatS.

Towards Revealing the Mystery behind Chain of Thought: a Theoretical Perspective

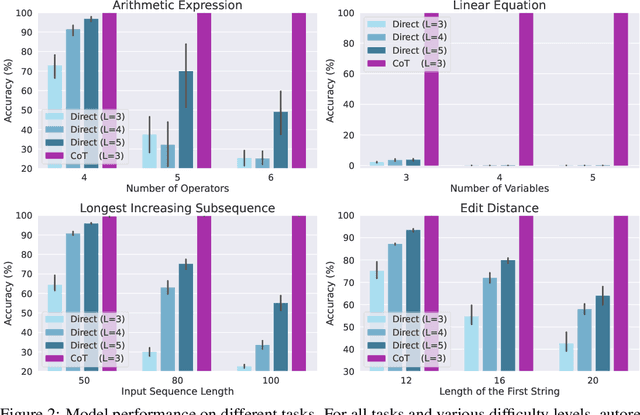
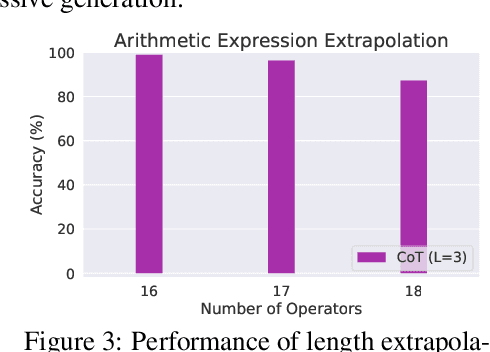
Recent studies have discovered that Chain-of-Thought prompting (CoT) can dramatically improve the performance of Large Language Models (LLMs), particularly when dealing with complex tasks involving mathematics or reasoning. Despite the enormous empirical success, the underlying mechanisms behind CoT and how it unlocks the potential of LLMs remain elusive. In this paper, we take a first step towards theoretically answering these questions. Specifically, we examine the capacity of LLMs with CoT in solving fundamental mathematical and decision-making problems. We start by giving an impossibility result showing that any bounded-depth Transformer cannot directly output correct answers for basic arithmetic/equation tasks unless the model size grows super-polynomially with respect to the input length. In contrast, we then prove by construction that autoregressive Transformers of a constant size suffice to solve both tasks by generating CoT derivations using a commonly-used math language format. Moreover, we show LLMs with CoT are capable of solving a general class of decision-making problems known as Dynamic Programming, thus justifying its power in tackling complex real-world tasks. Finally, extensive experiments on four tasks show that, while Transformers always fail to predict the answers directly, they can consistently learn to generate correct solutions step-by-step given sufficient CoT demonstrations.

Guided Diffusion Model for Adversarial Purification from Random Noise

In this paper, we propose a novel guided diffusion purification approach to provide a strong defense against adversarial attacks. Our model achieves 89.62% robust accuracy under PGD-L_inf attack (eps = 8/255) on the CIFAR-10 dataset. We first explore the essential correlations between unguided diffusion models and randomized smoothing, enabling us to apply the models to certified robustness. The empirical results show that our models outperform randomized smoothing by 5% when the certified L2 radius r is larger than 0.5.