Theoretical Benefit and Limitation of Diffusion Language Model

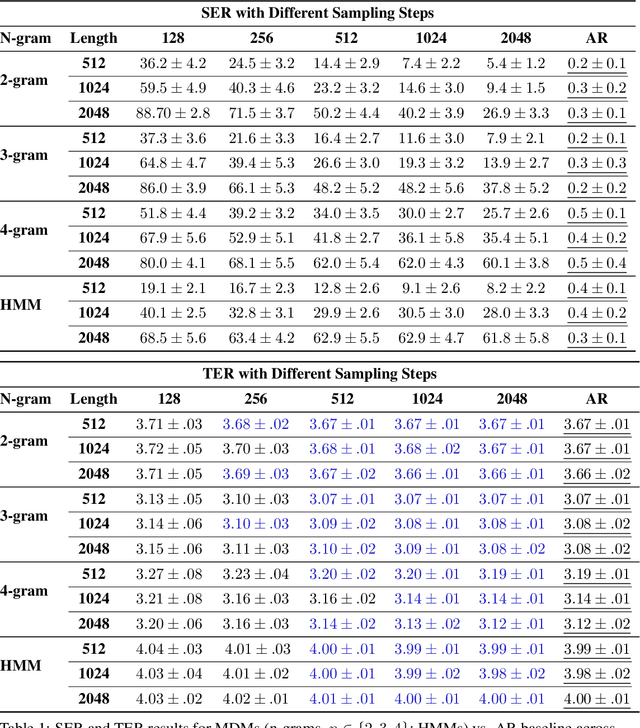
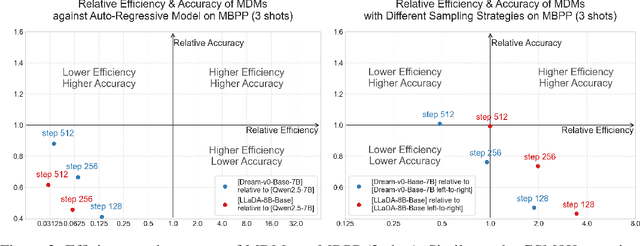
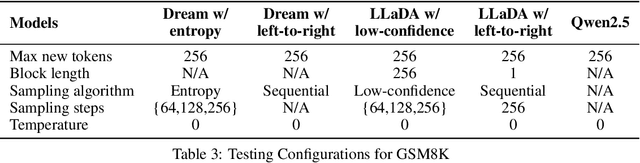
Diffusion language models have emerged as a promising approach for text generation. One would naturally expect this method to be an efficient replacement for autoregressive models since multiple tokens can be sampled in parallel during each diffusion step. However, its efficiency-accuracy trade-off is not yet well understood. In this paper, we present a rigorous theoretical analysis of a widely used type of diffusion language model, the Masked Diffusion Model (MDM), and find that its effectiveness heavily depends on the target evaluation metric. Under mild conditions, we prove that when using perplexity as the metric, MDMs can achieve near-optimal perplexity in sampling steps regardless of sequence length, demonstrating that efficiency can be achieved without sacrificing performance. However, when using the sequence error rate--which is important for understanding the "correctness" of a sequence, such as a reasoning chain--we show that the required sampling steps must scale linearly with sequence length to obtain "correct" sequences, thereby eliminating MDM's efficiency advantage over autoregressive models. Our analysis establishes the first theoretical foundation for understanding the benefits and limitations of MDMs. All theoretical findings are supported by empirical studies.

How Numerical Precision Affects Mathematical Reasoning Capabilities of LLMs

Despite the remarkable success of Transformer-based Large Language Models (LLMs) across various domains, understanding and enhancing their mathematical capabilities remains a significant challenge. In this paper, we conduct a rigorous theoretical analysis of LLMs' mathematical abilities, with a specific focus on their arithmetic performances. We identify numerical precision as a key factor that influences their effectiveness in mathematical tasks. Our results show that Transformers operating with low numerical precision fail to address arithmetic tasks, such as iterated addition and integer multiplication, unless the model size grows super-polynomially with respect to the input length. In contrast, Transformers with standard numerical precision can efficiently handle these tasks with significantly smaller model sizes. We further support our theoretical findings through empirical experiments that explore the impact of varying numerical precision on arithmetic tasks, providing valuable insights for improving the mathematical reasoning capabilities of LLMs.

DPO Meets PPO: Reinforced Token Optimization for RLHF

In the classical Reinforcement Learning from Human Feedback (RLHF) framework, Proximal Policy Optimization (PPO) is employed to learn from sparse, sentence-level rewards -- a challenging scenario in traditional deep reinforcement learning. Despite the great successes of PPO in the alignment of state-of-the-art closed-source large language models (LLMs), its open-source implementation is still largely sub-optimal, as widely reported by numerous research studies. To address these issues, we introduce a framework that models RLHF problems as a Markov decision process (MDP), enabling the capture of fine-grained token-wise information. Furthermore, we provide theoretical insights that demonstrate the superiority of our MDP framework over the previous sentence-level bandit formulation. Under this framework, we introduce an algorithm, dubbed as Reinforced Token Optimization (\texttt{RTO}), which learns the token-wise reward function from preference data and performs policy optimization based on this learned token-wise reward signal. Theoretically, \texttt{RTO} is proven to have the capability of finding the near-optimal policy sample-efficiently. For its practical implementation, \texttt{RTO} innovatively integrates Direct Preference Optimization (DPO) and PPO. DPO, originally derived from sparse sentence rewards, surprisingly provides us with a token-wise characterization of response quality, which is seamlessly incorporated into our subsequent PPO training stage. Extensive real-world alignment experiments verify the effectiveness of the proposed approach.

Do Efficient Transformers Really Save Computation?

As transformer-based language models are trained on increasingly large datasets and with vast numbers of parameters, finding more efficient alternatives to the standard Transformer has become very valuable. While many efficient Transformers and Transformer alternatives have been proposed, none provide theoretical guarantees that they are a suitable replacement for the standard Transformer. This makes it challenging to identify when to use a specific model and what directions to prioritize for further investigation. In this paper, we aim to understand the capabilities and limitations of efficient Transformers, specifically the Sparse Transformer and the Linear Transformer. We focus on their reasoning capability as exhibited by Chain-of-Thought (CoT) prompts and follow previous works to model them as Dynamic Programming (DP) problems. Our results show that while these models are expressive enough to solve general DP tasks, contrary to expectations, they require a model size that scales with the problem size. Nonetheless, we identify a class of DP problems for which these models can be more efficient than the standard Transformer. We confirm our theoretical results through experiments on representative DP tasks, adding to the understanding of efficient Transformers' practical strengths and weaknesses.

Two Stones Hit One Bird: Bilevel Positional Encoding for Better Length Extrapolation

In this work, we leverage the intrinsic segmentation of language sequences and design a new positional encoding method called Bilevel Positional Encoding (BiPE). For each position, our BiPE blends an intra-segment encoding and an inter-segment encoding. The intra-segment encoding identifies the locations within a segment and helps the model capture the semantic information therein via absolute positional encoding. The inter-segment encoding specifies the segment index, models the relationships between segments, and aims to improve extrapolation capabilities via relative positional encoding. Theoretical analysis shows this disentanglement of positional information makes learning more effective. The empirical results also show that our BiPE has superior length extrapolation capabilities across a wide range of tasks in diverse text modalities.

Rethinking Model-based, Policy-based, and Value-based Reinforcement Learning via the Lens of Representation Complexity

Reinforcement Learning (RL) encompasses diverse paradigms, including model-based RL, policy-based RL, and value-based RL, each tailored to approximate the model, optimal policy, and optimal value function, respectively. This work investigates the potential hierarchy of representation complexity -- the complexity of functions to be represented -- among these RL paradigms. We first demonstrate that, for a broad class of Markov decision processes (MDPs), the model can be represented by constant-depth circuits with polynomial size or Multi-Layer Perceptrons (MLPs) with constant layers and polynomial hidden dimension. However, the representation of the optimal policy and optimal value proves to be $\mathsf{NP}$-complete and unattainable by constant-layer MLPs with polynomial size. This demonstrates a significant representation complexity gap between model-based RL and model-free RL, which includes policy-based RL and value-based RL. To further explore the representation complexity hierarchy between policy-based RL and value-based RL, we introduce another general class of MDPs where both the model and optimal policy can be represented by constant-depth circuits with polynomial size or constant-layer MLPs with polynomial size. In contrast, representing the optimal value is $\mathsf{P}$-complete and intractable via a constant-layer MLP with polynomial hidden dimension. This accentuates the intricate representation complexity associated with value-based RL compared to policy-based RL. In summary, we unveil a potential representation complexity hierarchy within RL -- representing the model emerges as the easiest task, followed by the optimal policy, while representing the optimal value function presents the most intricate challenge.

Towards Revealing the Mystery behind Chain of Thought: a Theoretical Perspective

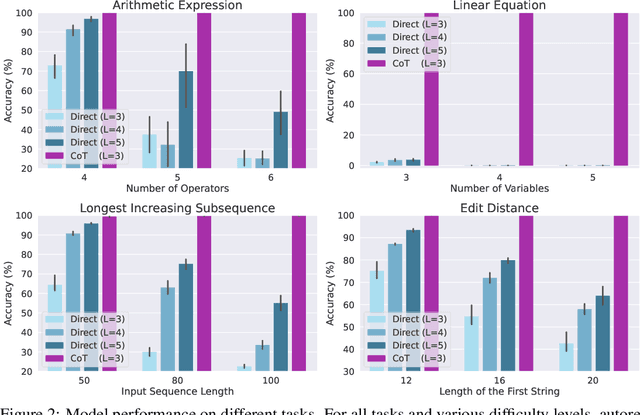
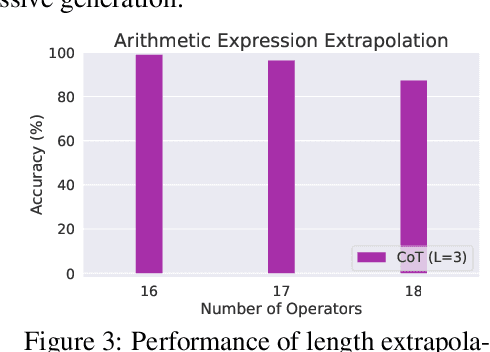
Recent studies have discovered that Chain-of-Thought prompting (CoT) can dramatically improve the performance of Large Language Models (LLMs), particularly when dealing with complex tasks involving mathematics or reasoning. Despite the enormous empirical success, the underlying mechanisms behind CoT and how it unlocks the potential of LLMs remain elusive. In this paper, we take a first step towards theoretically answering these questions. Specifically, we examine the capacity of LLMs with CoT in solving fundamental mathematical and decision-making problems. We start by giving an impossibility result showing that any bounded-depth Transformer cannot directly output correct answers for basic arithmetic/equation tasks unless the model size grows super-polynomially with respect to the input length. In contrast, we then prove by construction that autoregressive Transformers of a constant size suffice to solve both tasks by generating CoT derivations using a commonly-used math language format. Moreover, we show LLMs with CoT are capable of solving a general class of decision-making problems known as Dynamic Programming, thus justifying its power in tackling complex real-world tasks. Finally, extensive experiments on four tasks show that, while Transformers always fail to predict the answers directly, they can consistently learn to generate correct solutions step-by-step given sufficient CoT demonstrations.

A Complete Expressiveness Hierarchy for Subgraph GNNs via Subgraph Weisfeiler-Lehman Tests

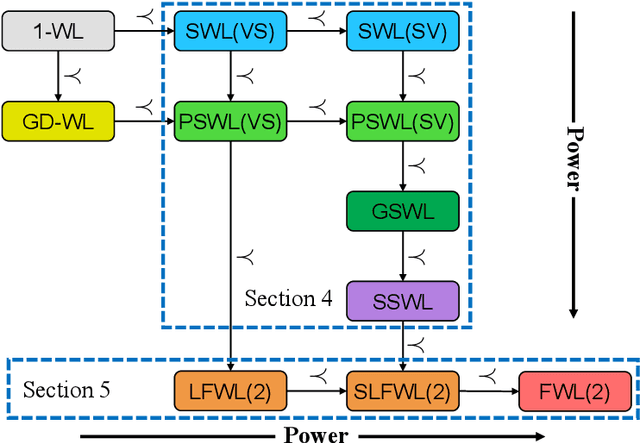
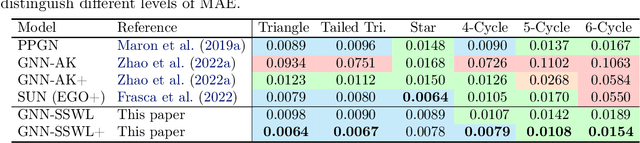
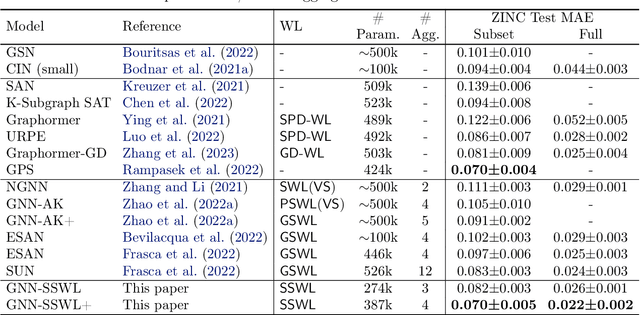
Recently, subgraph GNNs have emerged as an important direction for developing expressive graph neural networks (GNNs). While numerous architectures have been proposed, so far there is still a limited understanding of how various design paradigms differ in terms of expressive power, nor is it clear what design principle achieves maximal expressiveness with minimal architectural complexity. Targeting these fundamental questions, this paper conducts a systematic study of general node-based subgraph GNNs through the lens of Subgraph Weisfeiler-Lehman Tests (SWL). Our central result is to build a complete hierarchy of SWL with strictly growing expressivity. Concretely, we prove that any node-based subgraph GNN falls into one of the six SWL equivalence classes, among which $\mathsf{SSWL}$ achieves the maximal expressive power. We also study how these equivalence classes differ in terms of their practical expressiveness such as encoding graph distance and biconnectivity. In addition, we give a tight expressivity upper bound of all SWL algorithms by establishing a close relation with localized versions of Folklore WL tests (FWL). Overall, our results provide insights into the power of existing subgraph GNNs, guide the design of new architectures, and point out their limitations by revealing an inherent gap with the 2-FWL test. Finally, experiments on the ZINC benchmark demonstrate that $\mathsf{SSWL}$-inspired subgraph GNNs can significantly outperform prior architectures despite great simplicity.