A Complete Expressiveness Hierarchy for Subgraph GNNs via Subgraph Weisfeiler-Lehman Tests
Paper and Code
Feb 14, 2023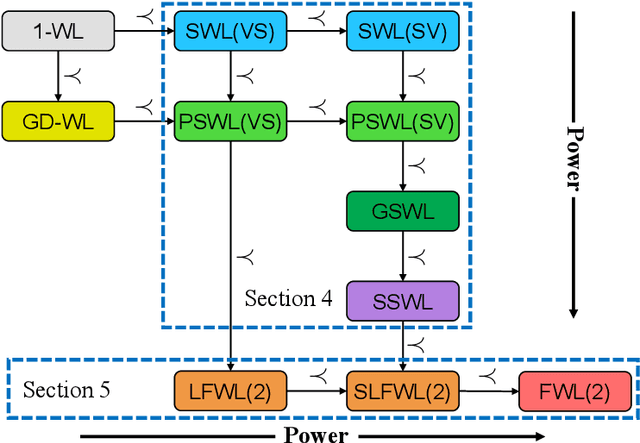
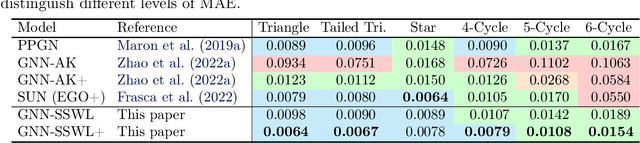
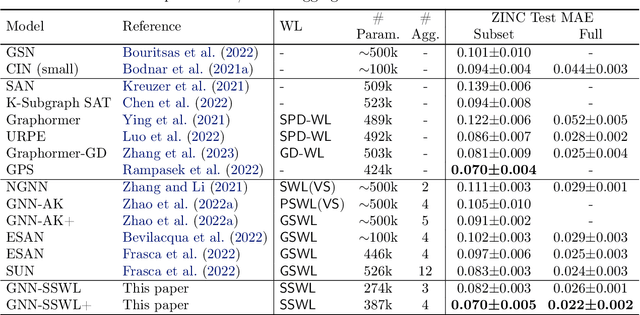
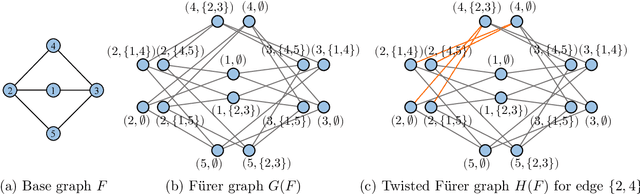
Recently, subgraph GNNs have emerged as an important direction for developing expressive graph neural networks (GNNs). While numerous architectures have been proposed, so far there is still a limited understanding of how various design paradigms differ in terms of expressive power, nor is it clear what design principle achieves maximal expressiveness with minimal architectural complexity. Targeting these fundamental questions, this paper conducts a systematic study of general node-based subgraph GNNs through the lens of Subgraph Weisfeiler-Lehman Tests (SWL). Our central result is to build a complete hierarchy of SWL with strictly growing expressivity. Concretely, we prove that any node-based subgraph GNN falls into one of the six SWL equivalence classes, among which $\mathsf{SSWL}$ achieves the maximal expressive power. We also study how these equivalence classes differ in terms of their practical expressiveness such as encoding graph distance and biconnectivity. In addition, we give a tight expressivity upper bound of all SWL algorithms by establishing a close relation with localized versions of Folklore WL tests (FWL). Overall, our results provide insights into the power of existing subgraph GNNs, guide the design of new architectures, and point out their limitations by revealing an inherent gap with the 2-FWL test. Finally, experiments on the ZINC benchmark demonstrate that $\mathsf{SSWL}$-inspired subgraph GNNs can significantly outperform prior architectures despite great simplicity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge