Muon in Associative Memory Learning: Training Dynamics and Scaling Laws

Muon updates matrix parameters via the matrix sign of the gradient and has shown strong empirical gains, yet its dynamics and scaling behavior remain unclear in theory. We study Muon in a linear associative memory model with softmax retrieval and a hierarchical frequency spectrum over query-answer pairs, with and without label noise. In this setting, we show that Gradient Descent (GD) learns frequency components at highly imbalanced rates, leading to slow convergence bottlenecked by low-frequency components. In contrast, the Muon optimizer mitigates this imbalance, leading to faster and more uniform progress. Specifically, in the noiseless case, Muon achieves an exponential speedup over GD; in the noisy case with a power-decay frequency spectrum, we derive Muon's optimization scaling law and demonstrate its superior scaling efficiency over GD. Furthermore, we show that Muon can be interpreted as an implicit matrix preconditioner arising from adaptive task alignment and block-symmetric gradient structure. In contrast, the preconditioner with coordinate-wise sign operator could match Muon under oracle access to unknown task representations, which is infeasible for SignGD in practice. Experiments on synthetic long-tail classification and LLaMA-style pre-training corroborate the theory.

Optimism Stabilizes Thompson Sampling for Adaptive Inference

Thompson sampling (TS) is widely used for stochastic multi-armed bandits, yet its inferential properties under adaptive data collection are subtle. Classical asymptotic theory for sample means can fail because arm-specific sample sizes are random and coupled with the rewards through the action-selection rule. We study this phenomenon in the $K$-armed Gaussian bandit and identify \emph{optimism} as a key mechanism for restoring \emph{stability}, a sufficient condition for valid asymptotic inference requiring each arm's pull count to concentrate around a deterministic scale. First, we prove that variance-inflated TS \citep{halder2025stable} is stable for any $K \ge 2$, including the challenging regime where multiple arms are optimal. This resolves the open question raised by \citet{halder2025stable} through extending their results from the two-armed setting to the general $K$-armed setting. Second, we analyze an alternative optimistic modification that keeps the posterior variance unchanged but adds an explicit mean bonus to posterior mean, and establish the same stability conclusion. In summary, suitably implemented optimism stabilizes Thompson sampling and enables asymptotically valid inference in multi-armed bandits, while incurring only a mild additional regret cost.

The Sample Complexity of Online Strategic Decision Making with Information Asymmetry and Knowledge Transportability

Information asymmetry is a pervasive feature of multi-agent systems, especially evident in economics and social sciences. In these settings, agents tailor their actions based on private information to maximize their rewards. These strategic behaviors often introduce complexities due to confounding variables. Simultaneously, knowledge transportability poses another significant challenge, arising from the difficulties of conducting experiments in target environments. It requires transferring knowledge from environments where empirical data is more readily available. Against these backdrops, this paper explores a fundamental question in online learning: Can we employ non-i.i.d. actions to learn about confounders even when requiring knowledge transfer? We present a sample-efficient algorithm designed to accurately identify system dynamics under information asymmetry and to navigate the challenges of knowledge transfer effectively in reinforcement learning, framed within an online strategic interaction model. Our method provably achieves learning of an $\epsilon$-optimal policy with a tight sample complexity of $O(1/\epsilon^2)$.

Less is More: Improving LLM Alignment via Preference Data Selection

Direct Preference Optimization (DPO) has emerged as a promising approach for aligning large language models with human preferences. While prior work mainly extends DPO from the aspect of the objective function, we instead improve DPO from the largely overlooked but critical aspect of data selection. Specifically, we address the issue of parameter shrinkage caused by noisy data by proposing a novel margin-maximization principle for dataset curation in DPO training. To accurately estimate margins for data selection, we propose a dual-margin guided approach that considers both external reward margins and implicit DPO reward margins. Extensive experiments demonstrate that our method reduces computational cost dramatically while improving performance. Remarkably, by using just 10\% of the Ultrafeedback dataset, our approach achieves 3\% to 8\% improvements across various Llama and Mistral series models on the AlpacaEval 2.0 benchmark. Furthermore, our approach seamlessly extends to iterative DPO, yielding a roughly 3\% improvement with 25\% online data, while further reducing training time. These results highlight the potential of data selection strategies for advancing preference optimization.

Learning an Optimal Assortment Policy under Observational Data

We study the fundamental problem of offline assortment optimization under the Multinomial Logit (MNL) model, where sellers must determine the optimal subset of the products to offer based solely on historical customer choice data. While most existing approaches to learning-based assortment optimization focus on the online learning of the optimal assortment through repeated interactions with customers, such exploration can be costly or even impractical in many real-world settings. In this paper, we consider the offline learning paradigm and investigate the minimal data requirements for efficient offline assortment optimization. To this end, we introduce Pessimistic Rank-Breaking (PRB), an algorithm that combines rank-breaking with pessimistic estimation. We prove that PRB is nearly minimax optimal by establishing the tight suboptimality upper bound and a nearly matching lower bound. This further shows that "optimal item coverage" - where each item in the optimal assortment appears sufficiently often in the historical data - is both sufficient and necessary for efficient offline learning. This significantly relaxes the previous requirement of observing the complete optimal assortment in the data. Our results provide fundamental insights into the data requirements for offline assortment optimization under the MNL model.

BRiTE: Bootstrapping Reinforced Thinking Process to Enhance Language Model Reasoning

Large Language Models (LLMs) have demonstrated remarkable capabilities in complex reasoning tasks, yet generating reliable reasoning processes remains a significant challenge. We present a unified probabilistic framework that formalizes LLM reasoning through a novel graphical model incorporating latent thinking processes and evaluation signals. Within this framework, we introduce the Bootstrapping Reinforced Thinking Process (BRiTE) algorithm, which works in two steps. First, it generates high-quality rationales by approximating the optimal thinking process through reinforcement learning, using a novel reward shaping mechanism. Second, it enhances the base LLM by maximizing the joint probability of rationale generation with respect to the model's parameters. Theoretically, we demonstrate BRiTE's convergence at a rate of $1/T$ with $T$ representing the number of iterations. Empirical evaluations on math and coding benchmarks demonstrate that our approach consistently improves performance across different base models without requiring human-annotated thinking processes. In addition, BRiTE demonstrates superior performance compared to existing algorithms that bootstrap thinking processes use alternative methods such as rejection sampling, and can even match or exceed the results achieved through supervised fine-tuning with human-annotated data.

A3S: A General Active Clustering Method with Pairwise Constraints

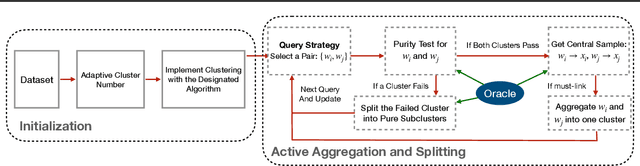
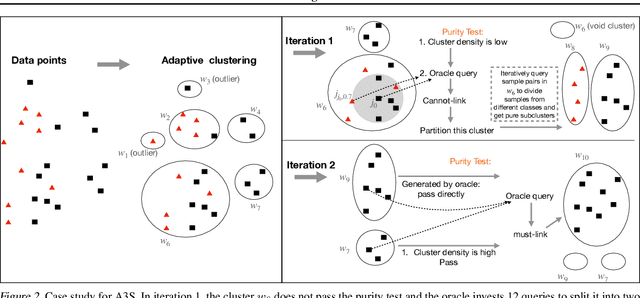
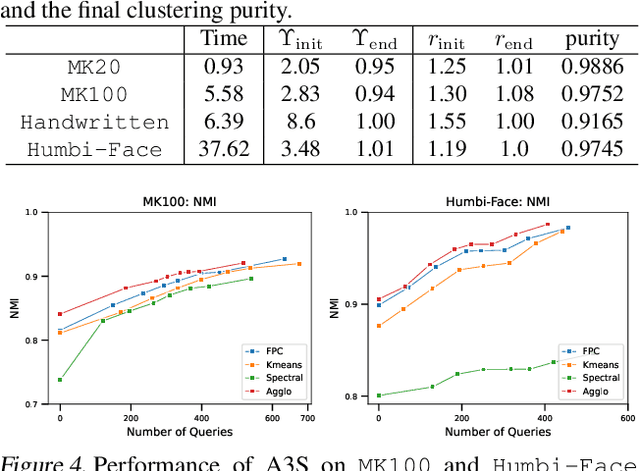
Active clustering aims to boost the clustering performance by integrating human-annotated pairwise constraints through strategic querying. Conventional approaches with semi-supervised clustering schemes encounter high query costs when applied to large datasets with numerous classes. To address these limitations, we propose a novel Adaptive Active Aggregation and Splitting (A3S) framework, falling within the cluster-adjustment scheme in active clustering. A3S features strategic active clustering adjustment on the initial cluster result, which is obtained by an adaptive clustering algorithm. In particular, our cluster adjustment is inspired by the quantitative analysis of Normalized mutual information gain under the information theory framework and can provably improve the clustering quality. The proposed A3S framework significantly elevates the performance and scalability of active clustering. In extensive experiments across diverse real-world datasets, A3S achieves desired results with significantly fewer human queries compared with existing methods.

Combinatorial Multivariant Multi-Armed Bandits with Applications to Episodic Reinforcement Learning and Beyond

We introduce a novel framework of combinatorial multi-armed bandits (CMAB) with multivariant and probabilistically triggering arms (CMAB-MT), where the outcome of each arm is a $d$-dimensional multivariant random variable and the feedback follows a general arm triggering process. Compared with existing CMAB works, CMAB-MT not only enhances the modeling power but also allows improved results by leveraging distinct statistical properties for multivariant random variables. For CMAB-MT, we propose a general 1-norm multivariant and triggering probability-modulated smoothness condition, and an optimistic CUCB-MT algorithm built upon this condition. Our framework can include many important problems as applications, such as episodic reinforcement learning (RL) and probabilistic maximum coverage for goods distribution, all of which meet the above smoothness condition and achieve matching or improved regret bounds compared to existing works. Through our new framework, we build the first connection between the episodic RL and CMAB literature, by offering a new angle to solve the episodic RL through the lens of CMAB, which may encourage more interactions between these two important directions.

DPO Meets PPO: Reinforced Token Optimization for RLHF

In the classical Reinforcement Learning from Human Feedback (RLHF) framework, Proximal Policy Optimization (PPO) is employed to learn from sparse, sentence-level rewards -- a challenging scenario in traditional deep reinforcement learning. Despite the great successes of PPO in the alignment of state-of-the-art closed-source large language models (LLMs), its open-source implementation is still largely sub-optimal, as widely reported by numerous research studies. To address these issues, we introduce a framework that models RLHF problems as a Markov decision process (MDP), enabling the capture of fine-grained token-wise information. Furthermore, we provide theoretical insights that demonstrate the superiority of our MDP framework over the previous sentence-level bandit formulation. Under this framework, we introduce an algorithm, dubbed as Reinforced Token Optimization (\texttt{RTO}), which learns the token-wise reward function from preference data and performs policy optimization based on this learned token-wise reward signal. Theoretically, \texttt{RTO} is proven to have the capability of finding the near-optimal policy sample-efficiently. For its practical implementation, \texttt{RTO} innovatively integrates Direct Preference Optimization (DPO) and PPO. DPO, originally derived from sparse sentence rewards, surprisingly provides us with a token-wise characterization of response quality, which is seamlessly incorporated into our subsequent PPO training stage. Extensive real-world alignment experiments verify the effectiveness of the proposed approach.

Sample-efficient Learning of Infinite-horizon Average-reward MDPs with General Function Approximation

We study infinite-horizon average-reward Markov decision processes (AMDPs) in the context of general function approximation. Specifically, we propose a novel algorithmic framework named Local-fitted Optimization with OPtimism (LOOP), which incorporates both model-based and value-based incarnations. In particular, LOOP features a novel construction of confidence sets and a low-switching policy updating scheme, which are tailored to the average-reward and function approximation setting. Moreover, for AMDPs, we propose a novel complexity measure -- average-reward generalized eluder coefficient (AGEC) -- which captures the challenge of exploration in AMDPs with general function approximation. Such a complexity measure encompasses almost all previously known tractable AMDP models, such as linear AMDPs and linear mixture AMDPs, and also includes newly identified cases such as kernel AMDPs and AMDPs with Bellman eluder dimensions. Using AGEC, we prove that LOOP achieves a sublinear $\tilde{\mathcal{O}}(\mathrm{poly}(d, \mathrm{sp}(V^*)) \sqrt{T\beta} )$ regret, where $d$ and $\beta$ correspond to AGEC and log-covering number of the hypothesis class respectively, $\mathrm{sp}(V^*)$ is the span of the optimal state bias function, $T$ denotes the number of steps, and $\tilde{\mathcal{O}} (\cdot) $ omits logarithmic factors. When specialized to concrete AMDP models, our regret bounds are comparable to those established by the existing algorithms designed specifically for these special cases. To the best of our knowledge, this paper presents the first comprehensive theoretical framework capable of handling nearly all AMDPs.