Semantic Caching for Low-Cost LLM Serving: From Offline Learning to Online Adaptation

Large Language Models (LLMs) are revolutionizing how users interact with information systems, yet their high inference cost poses serious scalability and sustainability challenges. Caching inference responses, allowing them to be retrieved without another forward pass through the LLM, has emerged as one possible solution. Traditional exact-match caching, however, overlooks the semantic similarity between queries, leading to unnecessary recomputation. Semantic caching addresses this by retrieving responses based on semantic similarity, but introduces a fundamentally different cache eviction problem: one must account for mismatch costs between incoming queries and cached responses. Moreover, key system parameters, such as query arrival probabilities and serving costs, are often unknown and must be learned over time. Existing semantic caching methods are largely ad-hoc, lacking theoretical foundations and unable to adapt to real-world uncertainty. In this paper, we present a principled, learning-based framework for semantic cache eviction under unknown query and cost distributions. We formulate both offline optimization and online learning variants of the problem, and develop provably efficient algorithms with state-of-the-art guarantees. We also evaluate our framework on a synthetic dataset, showing that our proposed algorithms perform matching or superior performance compared with baselines.

Near-Optimal Regret for Efficient Stochastic Combinatorial Semi-Bandits

The combinatorial multi-armed bandit (CMAB) is a cornerstone of sequential decision-making framework, dominated by two algorithmic families: UCB-based and adversarial methods such as follow the regularized leader (FTRL) and online mirror descent (OMD). However, prominent UCB-based approaches like CUCB suffer from additional regret factor $\log T$ that is detrimental over long horizons, while adversarial methods such as EXP3.M and HYBRID impose significant computational overhead. To resolve this trade-off, we introduce the Combinatorial Minimax Optimal Strategy in the Stochastic setting (CMOSS). CMOSS is a computationally efficient algorithm that achieves an instance-independent regret of $O\big( (\log k)^2\sqrt{kmT}\big )$ under semi-bandit feedback, where $m$ is the number of arms and $k$ is the maximum cardinality of a feasible action. Crucially, this result eliminates the dependency on $\log T$ and matches the established $\Omega\big( \sqrt{kmT}\big)$ lower bound up to $O\big((\log k)^2\big)$. We then extend our analysis to show that CMOSS is also applicable to cascading feedback. Experiments on synthetic and real-world datasets validate that CMOSS consistently outperforms benchmark algorithms in both regret and runtime efficiency.

Learning Best Paths in Quantum Networks

Quantum networks (QNs) transmit delicate quantum information across noisy quantum channels. Crucial applications, like quantum key distribution (QKD) and distributed quantum computation (DQC), rely on efficient quantum information transmission. Learning the best path between a pair of end nodes in a QN is key to enhancing such applications. This paper addresses learning the best path in a QN in the online learning setting. We explore two types of feedback: "link-level" and "path-level". Link-level feedback pertains to QNs with advanced quantum switches that enable link-level benchmarking. Path-level feedback, on the other hand, is associated with basic quantum switches that permit only path-level benchmarking. We introduce two online learning algorithms, BeQuP-Link and BeQuP-Path, to identify the best path using link-level and path-level feedback, respectively. To learn the best path, BeQuP-Link benchmarks the critical links dynamically, while BeQuP-Path relies on a subroutine, transferring path-level observations to estimate link-level parameters in a batch manner. We analyze the quantum resource complexity of these algorithms and demonstrate that both can efficiently and, with high probability, determine the best path. Finally, we perform NetSquid-based simulations and validate that both algorithms accurately and efficiently identify the best path.

A Unified Online-Offline Framework for Co-Branding Campaign Recommendations

Co-branding has become a vital strategy for businesses aiming to expand market reach within recommendation systems. However, identifying effective cross-industry partnerships remains challenging due to resource imbalances, uncertain brand willingness, and ever-changing market conditions. In this paper, we provide the first systematic study of this problem and propose a unified online-offline framework to enable co-branding recommendations. Our approach begins by constructing a bipartite graph linking ``initiating'' and ``target'' brands to quantify co-branding probabilities and assess market benefits. During the online learning phase, we dynamically update the graph in response to market feedback, while striking a balance between exploring new collaborations for long-term gains and exploiting established partnerships for immediate benefits. To address the high initial co-branding costs, our framework mitigates redundant exploration, thereby enhancing short-term performance while ensuring sustainable strategic growth. In the offline optimization phase, our framework consolidates the interests of multiple sub-brands under the same parent brand to maximize overall returns, avoid excessive investment in single sub-brands, and reduce unnecessary costs associated with over-prioritizing a single sub-brand. We present a theoretical analysis of our approach, establishing a highly nontrivial sublinear regret bound for online learning in the complex co-branding problem, and enhancing the approximation guarantee for the NP-hard offline budget allocation optimization. Experiments on both synthetic and real-world co-branding datasets demonstrate the practical effectiveness of our framework, with at least 12\% improvement.

Offline Clustering of Linear Bandits: Unlocking the Power of Clusters in Data-Limited Environments

Contextual linear multi-armed bandits are a learning framework for making a sequence of decisions, e.g., advertising recommendations for a sequence of arriving users. Recent works have shown that clustering these users based on the similarity of their learned preferences can significantly accelerate the learning. However, prior work has primarily focused on the online setting, which requires continually collecting user data, ignoring the offline data widely available in many applications. To tackle these limitations, we study the offline clustering of bandits (Off-ClusBand) problem, which studies how to use the offline dataset to learn cluster properties and improve decision-making across multiple users. The key challenge in Off-ClusBand arises from data insufficiency for users: unlike the online case, in the offline case, we have a fixed, limited dataset to work from and thus must determine whether we have enough data to confidently cluster users together. To address this challenge, we propose two algorithms: Off-C$^2$LUB, which we analytically show performs well for arbitrary amounts of user data, and Off-CLUB, which is prone to bias when data is limited but, given sufficient data, matches a theoretical lower bound that we derive for the offline clustered MAB problem. We experimentally validate these results on both real and synthetic datasets.

Fusing Reward and Dueling Feedback in Stochastic Bandits

This paper investigates the fusion of absolute (reward) and relative (dueling) feedback in stochastic bandits, where both feedback types are gathered in each decision round. We derive a regret lower bound, demonstrating that an efficient algorithm may incur only the smaller among the reward and dueling-based regret for each individual arm. We propose two fusion approaches: (1) a simple elimination fusion algorithm that leverages both feedback types to explore all arms and unifies collected information by sharing a common candidate arm set, and (2) a decomposition fusion algorithm that selects the more effective feedback to explore the corresponding arms and randomly assigns one feedback type for exploration and the other for exploitation in each round. The elimination fusion experiences a suboptimal multiplicative term of the number of arms in regret due to the intrinsic suboptimality of dueling elimination. In contrast, the decomposition fusion achieves regret matching the lower bound up to a constant under a common assumption. Extensive experiments confirm the efficacy of our algorithms and theoretical results.

Heterogeneous Multi-agent Multi-armed Bandits on Stochastic Block Models

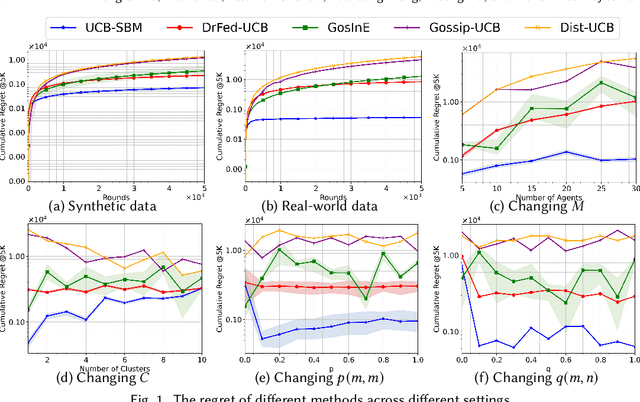
We study a novel heterogeneous multi-agent multi-armed bandit problem with a cluster structure induced by stochastic block models, influencing not only graph topology, but also reward heterogeneity. Specifically, agents are distributed on random graphs based on stochastic block models - a generalized Erdos-Renyi model with heterogeneous edge probabilities: agents are grouped into clusters (known or unknown); edge probabilities for agents within the same cluster differ from those across clusters. In addition, the cluster structure in stochastic block model also determines our heterogeneous rewards. Rewards distributions of the same arm vary across agents in different clusters but remain consistent within a cluster, unifying homogeneous and heterogeneous settings and varying degree of heterogeneity, and rewards are independent samples from these distributions. The objective is to minimize system-wide regret across all agents. To address this, we propose a novel algorithm applicable to both known and unknown cluster settings. The algorithm combines an averaging-based consensus approach with a newly introduced information aggregation and weighting technique, resulting in a UCB-type strategy. It accounts for graph randomness, leverages both intra-cluster (homogeneous) and inter-cluster (heterogeneous) information from rewards and graphs, and incorporates cluster detection for unknown cluster settings. We derive optimal instance-dependent regret upper bounds of order $\log{T}$ under sub-Gaussian rewards. Importantly, our regret bounds capture the degree of heterogeneity in the system (an additional layer of complexity), exhibit smaller constants, scale better for large systems, and impose significantly relaxed assumptions on edge probabilities. In contrast, prior works have not accounted for this refined problem complexity, rely on more stringent assumptions, and exhibit limited scalability.

Offline Learning for Combinatorial Multi-armed Bandits

The combinatorial multi-armed bandit (CMAB) is a fundamental sequential decision-making framework, extensively studied over the past decade. However, existing work primarily focuses on the online setting, overlooking the substantial costs of online interactions and the readily available offline datasets. To overcome these limitations, we introduce Off-CMAB, the first offline learning framework for CMAB. Central to our framework is the combinatorial lower confidence bound (CLCB) algorithm, which combines pessimistic reward estimations with combinatorial solvers. To characterize the quality of offline datasets, we propose two novel data coverage conditions and prove that, under these conditions, CLCB achieves a near-optimal suboptimality gap, matching the theoretical lower bound up to a logarithmic factor. We validate Off-CMAB through practical applications, including learning to rank, large language model (LLM) caching, and social influence maximization, showing its ability to handle nonlinear reward functions, general feedback models, and out-of-distribution action samples that excludes optimal or even feasible actions. Extensive experiments on synthetic and real-world datasets further highlight the superior performance of CLCB.

Combinatorial Logistic Bandits

We introduce a novel framework called combinatorial logistic bandits (CLogB), where in each round, a subset of base arms (called the super arm) is selected, with the outcome of each base arm being binary and its expectation following a logistic parametric model. The feedback is governed by a general arm triggering process. Our study covers CLogB with reward functions satisfying two smoothness conditions, capturing application scenarios such as online content delivery, online learning to rank, and dynamic channel allocation. We first propose a simple yet efficient algorithm, CLogUCB, utilizing a variance-agnostic exploration bonus. Under the 1-norm triggering probability modulated (TPM) smoothness condition, CLogUCB achieves a regret bound of $\tilde{O}(d\sqrt{\kappa KT})$, where $\tilde{O}$ ignores logarithmic factors, $d$ is the dimension of the feature vector, $\kappa$ represents the nonlinearity of the logistic model, and $K$ is the maximum number of base arms a super arm can trigger. This result improves on prior work by a factor of $\tilde{O}(\sqrt{\kappa})$. We then enhance CLogUCB with a variance-adaptive version, VA-CLogUCB, which attains a regret bound of $\tilde{O}(d\sqrt{KT})$ under the same 1-norm TPM condition, improving another $\tilde{O}(\sqrt{\kappa})$ factor. VA-CLogUCB shows even greater promise under the stronger triggering probability and variance modulated (TPVM) condition, achieving a leading $\tilde{O}(d\sqrt{T})$ regret, thus removing the additional dependency on the action-size $K$. Furthermore, we enhance the computational efficiency of VA-CLogUCB by eliminating the nonconvex optimization process when the context feature map is time-invariant while maintaining the tight $\tilde{O}(d\sqrt{T})$ regret. Finally, experiments on synthetic and real-world datasets demonstrate the superior performance of our algorithms compared to benchmark algorithms.

AxiomVision: Accuracy-Guaranteed Adaptive Visual Model Selection for Perspective-Aware Video Analytics

The rapid evolution of multimedia and computer vision technologies requires adaptive visual model deployment strategies to effectively handle diverse tasks and varying environments. This work introduces AxiomVision, a novel framework that can guarantee accuracy by leveraging edge computing to dynamically select the most efficient visual models for video analytics under diverse scenarios. Utilizing a tiered edge-cloud architecture, AxiomVision enables the deployment of a broad spectrum of visual models, from lightweight to complex DNNs, that can be tailored to specific scenarios while considering camera source impacts. In addition, AxiomVision provides three core innovations: (1) a dynamic visual model selection mechanism utilizing continual online learning, (2) an efficient online method that efficiently takes into account the influence of the camera's perspective, and (3) a topology-driven grouping approach that accelerates the model selection process. With rigorous theoretical guarantees, these advancements provide a scalable and effective solution for visual tasks inherent to multimedia systems, such as object detection, classification, and counting. Empirically, AxiomVision achieves a 25.7\% improvement in accuracy.