Heterogeneous Multi-agent Multi-armed Bandits on Stochastic Block Models

We study a novel heterogeneous multi-agent multi-armed bandit problem with a cluster structure induced by stochastic block models, influencing not only graph topology, but also reward heterogeneity. Specifically, agents are distributed on random graphs based on stochastic block models - a generalized Erdos-Renyi model with heterogeneous edge probabilities: agents are grouped into clusters (known or unknown); edge probabilities for agents within the same cluster differ from those across clusters. In addition, the cluster structure in stochastic block model also determines our heterogeneous rewards. Rewards distributions of the same arm vary across agents in different clusters but remain consistent within a cluster, unifying homogeneous and heterogeneous settings and varying degree of heterogeneity, and rewards are independent samples from these distributions. The objective is to minimize system-wide regret across all agents. To address this, we propose a novel algorithm applicable to both known and unknown cluster settings. The algorithm combines an averaging-based consensus approach with a newly introduced information aggregation and weighting technique, resulting in a UCB-type strategy. It accounts for graph randomness, leverages both intra-cluster (homogeneous) and inter-cluster (heterogeneous) information from rewards and graphs, and incorporates cluster detection for unknown cluster settings. We derive optimal instance-dependent regret upper bounds of order $\log{T}$ under sub-Gaussian rewards. Importantly, our regret bounds capture the degree of heterogeneity in the system (an additional layer of complexity), exhibit smaller constants, scale better for large systems, and impose significantly relaxed assumptions on edge probabilities. In contrast, prior works have not accounted for this refined problem complexity, rely on more stringent assumptions, and exhibit limited scalability.

Multi-agent Multi-armed Bandit with Fully Heavy-tailed Dynamics

We study decentralized multi-agent multi-armed bandits in fully heavy-tailed settings, where clients communicate over sparse random graphs with heavy-tailed degree distributions and observe heavy-tailed (homogeneous or heterogeneous) reward distributions with potentially infinite variance. The objective is to maximize system performance by pulling the globally optimal arm with the highest global reward mean across all clients. We are the first to address such fully heavy-tailed scenarios, which capture the dynamics and challenges in communication and inference among multiple clients in real-world systems. In homogeneous settings, our algorithmic framework exploits hub-like structures unique to heavy-tailed graphs, allowing clients to aggregate rewards and reduce noises via hub estimators when constructing UCB indices; under $M$ clients and degree distributions with power-law index $\alpha > 1$, our algorithm attains a regret bound (almost) of order $O(M^{1 -\frac{1}{\alpha}} \log{T})$. Under heterogeneous rewards, clients synchronize by communicating with neighbors, aggregating exchanged estimators in UCB indices; With our newly established information delay bounds on sparse random graphs, we prove a regret bound of $O(M \log{T})$. Our results improve upon existing work, which only address time-invariant connected graphs, or light-tailed dynamics in dense graphs and rewards.

Decentralized Blockchain-based Robust Multi-agent Multi-armed Bandit

We study a robust multi-agent multi-armed bandit problem where multiple clients or participants are distributed on a fully decentralized blockchain, with the possibility of some being malicious. The rewards of arms are homogeneous among the clients, following time-invariant stochastic distributions that are revealed to the participants only when the system is secure enough. The system's objective is to efficiently ensure the cumulative rewards gained by the honest participants. To this end and to the best of our knowledge, we are the first to incorporate advanced techniques from blockchains, as well as novel mechanisms, into the system to design optimal strategies for honest participants. This allows various malicious behaviors and the maintenance of participant privacy. More specifically, we randomly select a pool of validators who have access to all participants, design a brand-new consensus mechanism based on digital signatures for these validators, invent a UCB-based strategy that requires less information from participants through secure multi-party computation, and design the chain-participant interaction and an incentive mechanism to encourage participants' participation. Notably, we are the first to prove the theoretical guarantee of the proposed algorithms by regret analyses in the context of optimality in blockchains. Unlike existing work that integrates blockchains with learning problems such as federated learning which mainly focuses on numerical optimality, we demonstrate that the regret of honest participants is upper bounded by $log{T}$. This is consistent with the multi-agent multi-armed bandit problem without malicious participants and the robust multi-agent multi-armed bandit problem with purely Byzantine attacks.

Regret Lower Bounds in Multi-agent Multi-armed Bandit

Multi-armed Bandit motivates methods with provable upper bounds on regret and also the counterpart lower bounds have been extensively studied in this context. Recently, Multi-agent Multi-armed Bandit has gained significant traction in various domains, where individual clients face bandit problems in a distributed manner and the objective is the overall system performance, typically measured by regret. While efficient algorithms with regret upper bounds have emerged, limited attention has been given to the corresponding regret lower bounds, except for a recent lower bound for adversarial settings, which, however, has a gap with let known upper bounds. To this end, we herein provide the first comprehensive study on regret lower bounds across different settings and establish their tightness. Specifically, when the graphs exhibit good connectivity properties and the rewards are stochastically distributed, we demonstrate a lower bound of order $O(\log T)$ for instance-dependent bounds and $\sqrt{T}$ for mean-gap independent bounds which are tight. Assuming adversarial rewards, we establish a lower bound $O(T^{\frac{2}{3}})$ for connected graphs, thereby bridging the gap between the lower and upper bound in the prior work. We also show a linear regret lower bound when the graph is disconnected. While previous works have explored these settings with upper bounds, we provide a thorough study on tight lower bounds.

Decentralized Randomly Distributed Multi-agent Multi-armed Bandit with Heterogeneous Rewards

We study a decentralized multi-agent multi-armed bandit problem in which multiple clients are connected by time dependent random graphs provided by an environment. The reward distributions of each arm vary across clients and rewards are generated independently over time by an environment based on distributions that include both sub-exponential and sub-gaussian distributions. Each client pulls an arm and communicates with neighbors based on the graph provided by the environment. The goal is to minimize the overall regret of the entire system through collaborations. To this end, we introduce a novel algorithmic framework, which first provides robust simulation methods for generating random graphs using rapidly mixing Markov chains or the random graph model, and then combines an averaging-based consensus approach with a newly proposed weighting technique and the upper confidence bound to deliver a UCB-type solution. Our algorithms account for the randomness in the graphs, removing the conventional doubly stochasticity assumption, and only require the knowledge of the number of clients at initialization. We derive optimal instance-dependent regret upper bounds of order $\log{T}$ in both sub-gaussian and sub-exponential environments, and a nearly optimal mean-gap independent regret upper bound of order $\sqrt{T}\log T$ up to a $\log T$ factor. Importantly, our regret bounds hold with high probability and capture graph randomness, whereas prior works consider expected regret under assumptions and require more stringent reward distributions.

Pareto Regret Analyses in Multi-objective Multi-armed Bandit

We study Pareto optimality in multi-objective multi-armed bandit by providing a formulation of adversarial multi-objective multi-armed bandit and properly defining its Pareto regrets that can be generalized to stochastic settings as well. The regrets do not rely on any scalarization functions and reflect Pareto optimality compared to scalarized regrets. We also present new algorithms assuming both with and without prior information of the multi-objective multi-armed bandit setting. The algorithms are shown optimal in adversarial settings and nearly optimal in stochastic settings simultaneously by our established upper bounds and lower bounds on Pareto regrets. Moreover, the lower bound analyses show that the new regrets are consistent with the existing Pareto regret for stochastic settings and extend an adversarial attack mechanism from bandit to the multi-objective one.

GCF: Generalized Causal Forest for Heterogeneous Treatment Effect Estimation in Online Marketplace

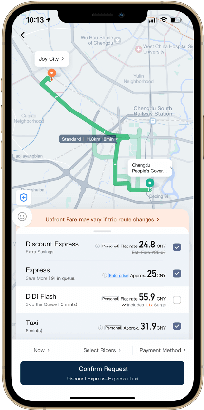
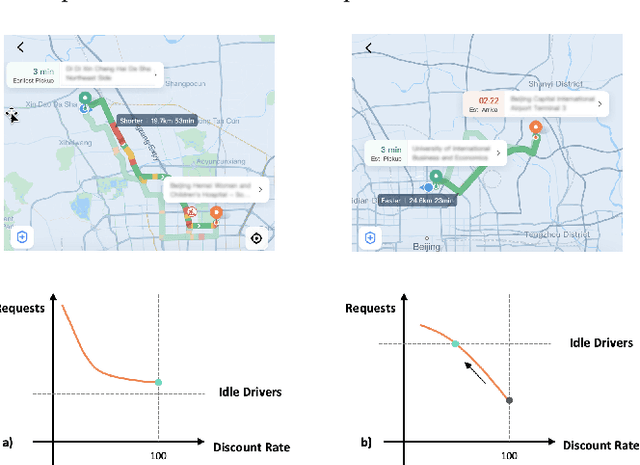
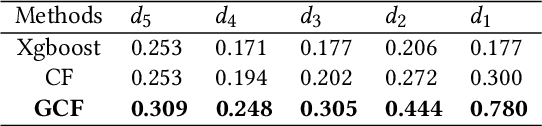
Uplift modeling is a rapidly growing approach that utilizes machine learning and causal inference methods to estimate the heterogeneous treatment effects. It has been widely adopted and applied to online marketplaces to assist large-scale decision-making in recent years. The existing popular methods, like forest-based modeling, either work only for discrete treatments or make partially linear or parametric assumptions that may suffer from model misspecification. To alleviate these problems, we extend causal forest (CF) with non-parametric dose-response functions (DRFs) that can be estimated locally using a kernel-based doubly robust estimator. Moreover, we propose a distance-based splitting criterion in the functional space of conditional DRFs to capture the heterogeneity for the continuous treatments. We call the proposed algorithm generalized causal forest (GCF) as it generalizes the use case of CF to a much broader setup. We show the effectiveness of GCF by comparing it to popular uplift modeling models on both synthetic and real-world datasets. We implement GCF in Spark and successfully deploy it into DiDi's real-time pricing system. Online A/B testing results further validate the superiority of GCF.

Regret Bounds and Reinforcement Learning Exploration of EXP-based Algorithms

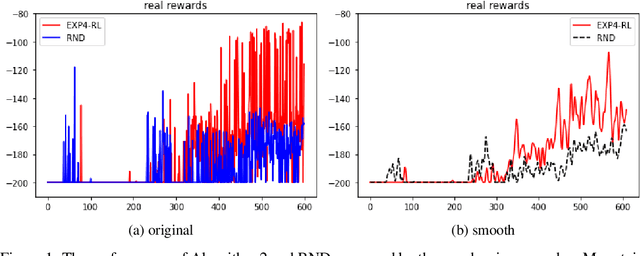
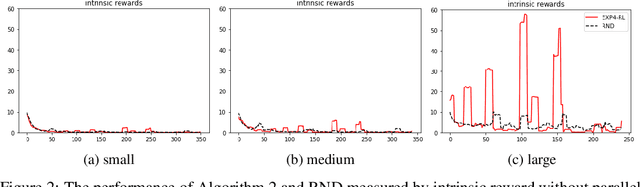
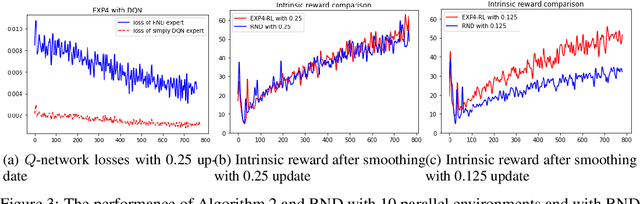
EXP-based algorithms are often used for exploration in multi-armed bandit. We revisit the EXP3.P algorithm and establish both the lower and upper bounds of regret in the Gaussian multi-armed bandit setting, as well as a more general distribution option. The analyses do not require bounded rewards compared to classical regret assumptions. We also extend EXP4 from multi-armed bandit to reinforcement learning to incentivize exploration by multiple agents. The resulting algorithm has been tested on hard-to-explore games and it shows an improvement on exploration compared to state-of-the-art.