Mohammad Hajiesmaili
Degradation-Aware Frequency Regulation of a Heterogeneous Battery Fleet via Reinforcement Learning
Jan 30, 2026Abstract:Battery energy storage systems are increasingly deployed as fast-responding resources for grid balancing services such as frequency regulation and for mitigating renewable generation uncertainty. However, repeated charging and discharging induces cycling degradation and reduces battery lifetime. This paper studies the real-time scheduling of a heterogeneous battery fleet that collectively tracks a stochastic balancing signal subject to per-battery ramp-rate and capacity constraints, while minimizing long-term cycling degradation. Cycling degradation is fundamentally path-dependent: it is determined by charge-discharge cycles formed by the state-of-charge (SoC) trajectory and is commonly quantified via rainflow cycle counting. This non-Markovian structure makes it difficult to express degradation as an additive per-time-step cost, complicating classical dynamic programming approaches. We address this challenge by formulating the fleet scheduling problem as a Markov decision process (MDP) with constrained action space and designing a dense proxy reward that provides informative feedback at each time step while remaining aligned with long-term cycle-depth reduction. To scale learning to large state-action spaces induced by fine-grained SoC discretization and asymmetric per-battery constraints, we develop a function-approximation reinforcement learning method using an Extreme Learning Machine (ELM) as a random nonlinear feature map combined with linear temporal-difference learning. We evaluate the proposed approach on a toy Markovian signal model and on a Markovian model trained from real-world regulation signal traces obtained from the University of Delaware, and demonstrate consistent reductions in cycle-depth occurrence and degradation metrics compared to baseline scheduling policies.
The Secretary Problem with Predictions and a Chosen Order
Jan 12, 2026Abstract:We study a learning-augmented variant of the secretary problem, recently introduced by Fujii and Yoshida (2023), in which the decision-maker has access to machine-learned predictions of candidate values. The central challenge is to balance consistency and robustness: when predictions are accurate, the algorithm should select a near-optimal secretary, while under inaccurate predictions it should still guarantee a bounded competitive ratio. We consider both the classical Random Order Secretary Problem (ROSP), where candidates arrive in a uniformly random order, and a more natural learning-augmented model in which the decision-maker may choose the arrival order based on predicted values. We call this model the Chosen Order Secretary Problem (COSP), capturing scenarios such as interview schedules set in advance. We propose a new randomized algorithm applicable to both ROSP and COSP. Our method switches from fully trusting predictions to a threshold-based rule once a large prediction deviation is detected. Let $ε\in [0,1]$ denote the maximum multiplicative prediction error. For ROSP, our algorithm achieves a competitive ratio of $\max\{0.221, (1-ε)/(1+ε)\}$, improving upon the prior bound of $\max\{0.215, (1-ε)/(1+ε)\}$. For COSP, we achieve $\max\{0.262, (1-ε)/(1+ε)\}$, surpassing the $0.25$ worst-case bound for prior approaches and moving closer to the classical secretary benchmark of $1/e \approx 0.368$. These results highlight the benefit of combining predictions with arrival-order control in online decision-making.
Offline Clustering of Preference Learning with Active-data Augmentation
Oct 30, 2025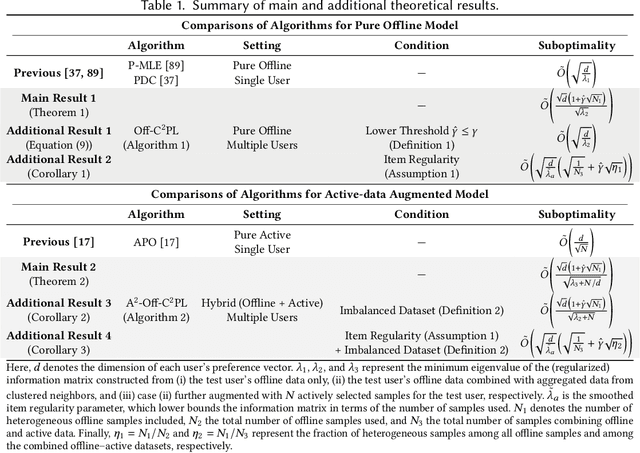
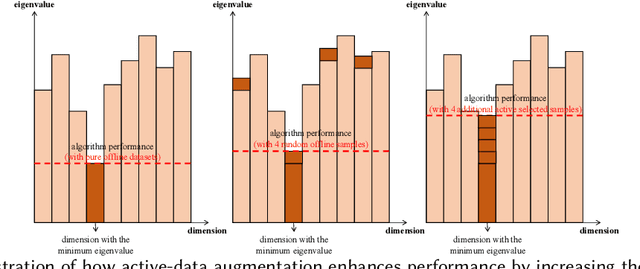

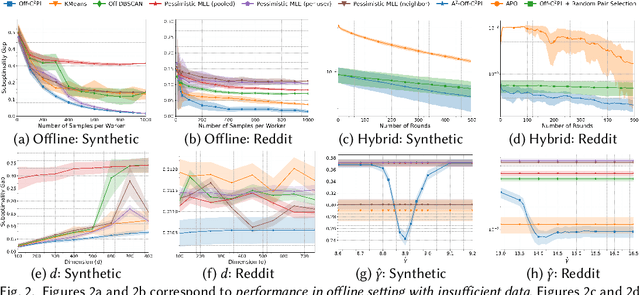
Abstract:Preference learning from pairwise feedback is a widely adopted framework in applications such as reinforcement learning with human feedback and recommendations. In many practical settings, however, user interactions are limited or costly, making offline preference learning necessary. Moreover, real-world preference learning often involves users with different preferences. For example, annotators from different backgrounds may rank the same responses differently. This setting presents two central challenges: (1) identifying similarity across users to effectively aggregate data, especially under scenarios where offline data is imbalanced across dimensions, and (2) handling the imbalanced offline data where some preference dimensions are underrepresented. To address these challenges, we study the Offline Clustering of Preference Learning problem, where the learner has access to fixed datasets from multiple users with potentially different preferences and aims to maximize utility for a test user. To tackle the first challenge, we first propose Off-C$^2$PL for the pure offline setting, where the learner relies solely on offline data. Our theoretical analysis provides a suboptimality bound that explicitly captures the tradeoff between sample noise and bias. To address the second challenge of inbalanced data, we extend our framework to the setting with active-data augmentation where the learner is allowed to select a limited number of additional active-data for the test user based on the cluster structure learned by Off-C$^2$PL. In this setting, our second algorithm, A$^2$-Off-C$^2$PL, actively selects samples that target the least-informative dimensions of the test user's preference. We prove that these actively collected samples contribute more effectively than offline ones. Finally, we validate our theoretical results through simulations on synthetic and real-world datasets.
Signal-Aware Workload Shifting Algorithms with Uncertainty-Quantified Predictors
Sep 30, 2025Abstract:A wide range of sustainability and grid-integration strategies depend on workload shifting, which aligns the timing of energy consumption with external signals such as grid curtailment events, carbon intensity, or time-of-use electricity prices. The main challenge lies in the online nature of the problem: operators must make real-time decisions (e.g., whether to consume energy now) without knowledge of the future. While forecasts of signal values are typically available, prior work on learning-augmented online algorithms has relied almost exclusively on simple point forecasts. In parallel, the forecasting research has made significant progress in uncertainty quantification (UQ), which provides richer and more fine-grained predictive information. In this paper, we study how online workload shifting can leverage UQ predictors to improve decision-making. We introduce $\texttt{UQ-Advice}$, a learning-augmented algorithm that systematically integrates UQ forecasts through a $\textit{decision uncertainty score}$ that measures how forecast uncertainty affects optimal future decisions. By introducing $\textit{UQ-robustness}$, a new metric that characterizes how performance degrades with forecast uncertainty, we establish theoretical performance guarantees for $\texttt{UQ-Advice}$. Finally, using trace-driven experiments on carbon intensity and electricity price data, we demonstrate that $\texttt{UQ-Advice}$ consistently outperforms robust baselines and existing learning-augmented methods that ignore uncertainty.
Learning Best Paths in Quantum Networks
Jun 14, 2025Abstract:Quantum networks (QNs) transmit delicate quantum information across noisy quantum channels. Crucial applications, like quantum key distribution (QKD) and distributed quantum computation (DQC), rely on efficient quantum information transmission. Learning the best path between a pair of end nodes in a QN is key to enhancing such applications. This paper addresses learning the best path in a QN in the online learning setting. We explore two types of feedback: "link-level" and "path-level". Link-level feedback pertains to QNs with advanced quantum switches that enable link-level benchmarking. Path-level feedback, on the other hand, is associated with basic quantum switches that permit only path-level benchmarking. We introduce two online learning algorithms, BeQuP-Link and BeQuP-Path, to identify the best path using link-level and path-level feedback, respectively. To learn the best path, BeQuP-Link benchmarks the critical links dynamically, while BeQuP-Path relies on a subroutine, transferring path-level observations to estimate link-level parameters in a batch manner. We analyze the quantum resource complexity of these algorithms and demonstrate that both can efficiently and, with high probability, determine the best path. Finally, we perform NetSquid-based simulations and validate that both algorithms accurately and efficiently identify the best path.
Offline Clustering of Linear Bandits: Unlocking the Power of Clusters in Data-Limited Environments
May 25, 2025Abstract:Contextual linear multi-armed bandits are a learning framework for making a sequence of decisions, e.g., advertising recommendations for a sequence of arriving users. Recent works have shown that clustering these users based on the similarity of their learned preferences can significantly accelerate the learning. However, prior work has primarily focused on the online setting, which requires continually collecting user data, ignoring the offline data widely available in many applications. To tackle these limitations, we study the offline clustering of bandits (Off-ClusBand) problem, which studies how to use the offline dataset to learn cluster properties and improve decision-making across multiple users. The key challenge in Off-ClusBand arises from data insufficiency for users: unlike the online case, in the offline case, we have a fixed, limited dataset to work from and thus must determine whether we have enough data to confidently cluster users together. To address this challenge, we propose two algorithms: Off-C$^2$LUB, which we analytically show performs well for arbitrary amounts of user data, and Off-CLUB, which is prone to bias when data is limited but, given sufficient data, matches a theoretical lower bound that we derive for the offline clustered MAB problem. We experimentally validate these results on both real and synthetic datasets.
Fusing Reward and Dueling Feedback in Stochastic Bandits
Apr 22, 2025Abstract:This paper investigates the fusion of absolute (reward) and relative (dueling) feedback in stochastic bandits, where both feedback types are gathered in each decision round. We derive a regret lower bound, demonstrating that an efficient algorithm may incur only the smaller among the reward and dueling-based regret for each individual arm. We propose two fusion approaches: (1) a simple elimination fusion algorithm that leverages both feedback types to explore all arms and unifies collected information by sharing a common candidate arm set, and (2) a decomposition fusion algorithm that selects the more effective feedback to explore the corresponding arms and randomly assigns one feedback type for exploration and the other for exploitation in each round. The elimination fusion experiences a suboptimal multiplicative term of the number of arms in regret due to the intrinsic suboptimality of dueling elimination. In contrast, the decomposition fusion achieves regret matching the lower bound up to a constant under a common assumption. Extensive experiments confirm the efficacy of our algorithms and theoretical results.
Heterogeneous Multi-Agent Bandits with Parsimonious Hints
Feb 22, 2025



Abstract:We study a hinted heterogeneous multi-agent multi-armed bandits problem (HMA2B), where agents can query low-cost observations (hints) in addition to pulling arms. In this framework, each of the $M$ agents has a unique reward distribution over $K$ arms, and in $T$ rounds, they can observe the reward of the arm they pull only if no other agent pulls that arm. The goal is to maximize the total utility by querying the minimal necessary hints without pulling arms, achieving time-independent regret. We study HMA2B in both centralized and decentralized setups. Our main centralized algorithm, GP-HCLA, which is an extension of HCLA, uses a central decision-maker for arm-pulling and hint queries, achieving $O(M^4K)$ regret with $O(MK\log T)$ adaptive hints. In decentralized setups, we propose two algorithms, HD-ETC and EBHD-ETC, that allow agents to choose actions independently through collision-based communication and query hints uniformly until stopping, yielding $O(M^3K^2)$ regret with $O(M^3K\log T)$ hints, where the former requires knowledge of the minimum gap and the latter does not. Finally, we establish lower bounds to prove the optimality of our results and verify them through numerical simulations.
Heterogeneous Multi-agent Multi-armed Bandits on Stochastic Block Models
Feb 11, 2025
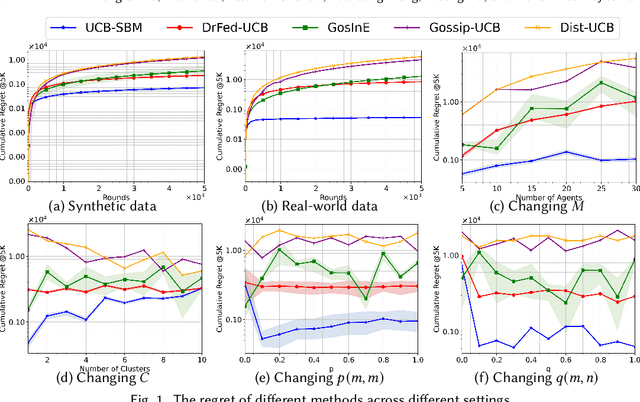
Abstract:We study a novel heterogeneous multi-agent multi-armed bandit problem with a cluster structure induced by stochastic block models, influencing not only graph topology, but also reward heterogeneity. Specifically, agents are distributed on random graphs based on stochastic block models - a generalized Erdos-Renyi model with heterogeneous edge probabilities: agents are grouped into clusters (known or unknown); edge probabilities for agents within the same cluster differ from those across clusters. In addition, the cluster structure in stochastic block model also determines our heterogeneous rewards. Rewards distributions of the same arm vary across agents in different clusters but remain consistent within a cluster, unifying homogeneous and heterogeneous settings and varying degree of heterogeneity, and rewards are independent samples from these distributions. The objective is to minimize system-wide regret across all agents. To address this, we propose a novel algorithm applicable to both known and unknown cluster settings. The algorithm combines an averaging-based consensus approach with a newly introduced information aggregation and weighting technique, resulting in a UCB-type strategy. It accounts for graph randomness, leverages both intra-cluster (homogeneous) and inter-cluster (heterogeneous) information from rewards and graphs, and incorporates cluster detection for unknown cluster settings. We derive optimal instance-dependent regret upper bounds of order $\log{T}$ under sub-Gaussian rewards. Importantly, our regret bounds capture the degree of heterogeneity in the system (an additional layer of complexity), exhibit smaller constants, scale better for large systems, and impose significantly relaxed assumptions on edge probabilities. In contrast, prior works have not accounted for this refined problem complexity, rely on more stringent assumptions, and exhibit limited scalability.
Towards Environmentally Equitable AI
Dec 21, 2024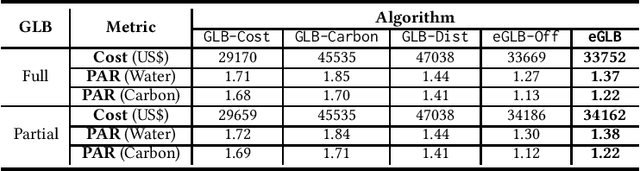
Abstract:The skyrocketing demand for artificial intelligence (AI) has created an enormous appetite for globally deployed power-hungry servers. As a result, the environmental footprint of AI systems has come under increasing scrutiny. More crucially, the current way that we exploit AI workloads' flexibility and manage AI systems can lead to wildly different environmental impacts across locations, increasingly raising environmental inequity concerns and creating unintended sociotechnical consequences. In this paper, we advocate environmental equity as a priority for the management of future AI systems, advancing the boundaries of existing resource management for sustainable AI and also adding a unique dimension to AI fairness. Concretely, we uncover the potential of equity-aware geographical load balancing to fairly re-distribute the environmental cost across different regions, followed by algorithmic challenges. We conclude by discussing a few future directions to exploit the full potential of system management approaches to mitigate AI's environmental inequity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge