Distance Adaptive Beam Search for Provably Accurate Graph-Based Nearest Neighbor Search

Nearest neighbor search is central in machine learning, information retrieval, and databases. For high-dimensional datasets, graph-based methods such as HNSW, DiskANN, and NSG have become popular thanks to their empirical accuracy and efficiency. These methods construct a directed graph over the dataset and perform beam search on the graph to find nodes close to a given query. While significant work has focused on practical refinements and theoretical understanding of graph-based methods, many questions remain. We propose a new distance-based termination condition for beam search to replace the commonly used condition based on beam width. We prove that, as long as the search graph is navigable, our resulting Adaptive Beam Search method is guaranteed to approximately solve the nearest-neighbor problem, establishing a connection between navigability and the performance of graph-based search. We also provide extensive experiments on our new termination condition for both navigable graphs and approximately navigable graphs used in practice, such as HNSW and Vamana graphs. We find that Adaptive Beam Search outperforms standard beam search over a range of recall values, data sets, graph constructions, and target number of nearest neighbors. It thus provides a simple and practical way to improve the performance of popular methods.

Efficient and Private Marginal Reconstruction with Local Non-Negativity

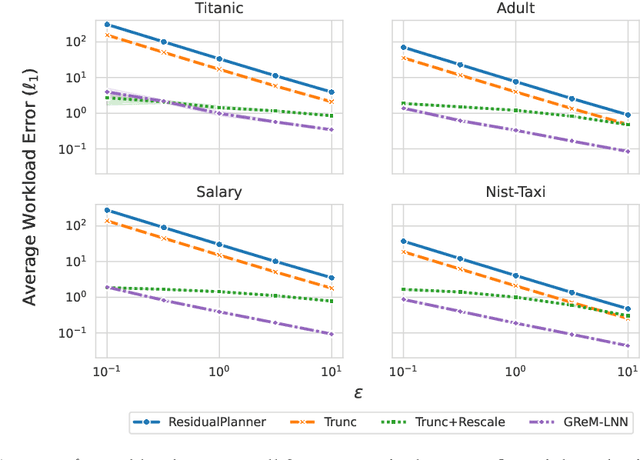
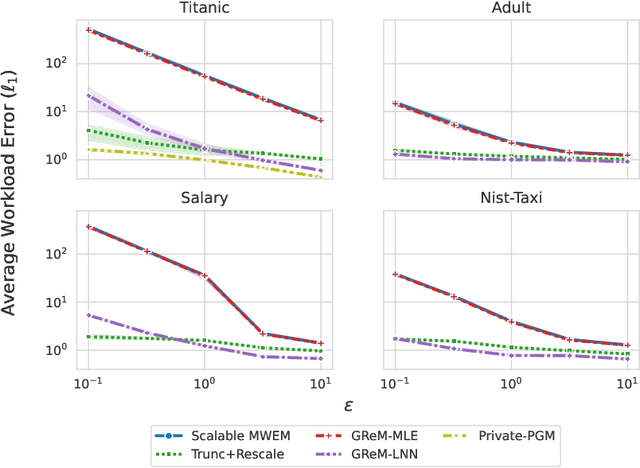
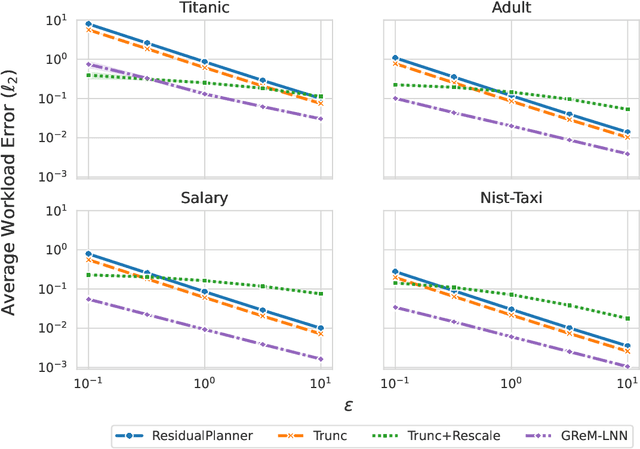
Differential privacy is the dominant standard for formal and quantifiable privacy and has been used in major deployments that impact millions of people. Many differentially private algorithms for query release and synthetic data contain steps that reconstruct answers to queries from answers to other queries measured by the mechanism. Reconstruction is an important subproblem for such mechanisms to economize the privacy budget, minimize error on reconstructed answers, and allow for scalability to high-dimensional datasets. In this paper, we introduce a principled and efficient postprocessing method ReM (Residuals-to-Marginals) for reconstructing answers to marginal queries. Our method builds on recent work on efficient mechanisms for marginal query release, based on making measurements using a residual query basis that admits efficient pseudoinversion, which is an important primitive used in reconstruction. An extension GReM-LNN (Gaussian Residuals-to-Marginals with Local Non-negativity) reconstructs marginals under Gaussian noise satisfying consistency and non-negativity, which often reduces error on reconstructed answers. We demonstrate the utility of ReM and GReM-LNN by applying them to improve existing private query answering mechanisms: ResidualPlanner and MWEM.

Sharper Bounds for Chebyshev Moment Matching with Applications to Differential Privacy and Beyond

We study the problem of approximately recovering a probability distribution given noisy measurements of its Chebyshev polynomial moments. We sharpen prior work, proving that accurate recovery in the Wasserstein distance is possible with more noise than previously known. As a main application, our result yields a simple "linear query" algorithm for constructing a differentially private synthetic data distribution with Wasserstein-1 error $\tilde{O}(1/n)$ based on a dataset of $n$ points in $[-1,1]$. This bound is optimal up to log factors and matches a recent breakthrough of Boedihardjo, Strohmer, and Vershynin [Probab. Theory. Rel., 2024], which uses a more complex "superregular random walk" method to beat an $O(1/\sqrt{n})$ accuracy barrier inherent to earlier approaches. We illustrate a second application of our new moment-based recovery bound in numerical linear algebra: by improving an approach of Braverman, Krishnan, and Musco [STOC 2022], our result yields a faster algorithm for estimating the spectral density of a symmetric matrix up to small error in the Wasserstein distance.

Competitive Algorithms for Online Knapsack with Succinct Predictions

In the online knapsack problem, the goal is to pack items arriving online with different values and weights into a capacity-limited knapsack to maximize the total value of the accepted items. We study \textit{learning-augmented} algorithms for this problem, which aim to use machine-learned predictions to move beyond pessimistic worst-case guarantees. Existing learning-augmented algorithms for online knapsack consider relatively complicated prediction models that give an algorithm substantial information about the input, such as the total weight of items at each value. In practice, such predictions can be error-sensitive and difficult to learn. Motivated by this limitation, we introduce a family of learning-augmented algorithms for online knapsack that use \emph{succinct predictions}. In particular, the machine-learned prediction given to the algorithm is just a single value or interval that estimates the minimum value of any item accepted by an offline optimal solution. By leveraging a relaxation to online \emph{fractional} knapsack, we design algorithms that can leverage such succinct predictions in both the trusted setting (i.e., with perfect prediction) and the untrusted setting, where we prove that a simple meta-algorithm achieves a nearly optimal consistency-robustness trade-off. Empirically, we show that our algorithms significantly outperform baselines that do not use predictions and often outperform algorithms based on more complex prediction models.

Navigable Graphs for High-Dimensional Nearest Neighbor Search: Constructions and Limits

There has been significant recent interest in graph-based nearest neighbor search methods, many of which are centered on the construction of navigable graphs over high-dimensional point sets. A graph is navigable if we can successfully move from any starting node to any target node using a greedy routing strategy where we always move to the neighbor that is closest to the destination according to a given distance function. The complete graph is navigable for any point set, but the important question for applications is if sparser graphs can be constructed. While this question is fairly well understood in low-dimensions, we establish some of the first upper and lower bounds for high-dimensional point sets. First, we give a simple and efficient way to construct a navigable graph with average degree $O(\sqrt{n \log n })$ for any set of $n$ points, in any dimension, for any distance function. We compliment this result with a nearly matching lower bound: even under the Euclidean metric in $O(\log n)$ dimensions, a random point set has no navigable graph with average degree $O(n^{\alpha})$ for any $\alpha < 1/2$. Our lower bound relies on sharp anti-concentration bounds for binomial random variables, which we use to show that the near-neighborhoods of a set of random points do not overlap significantly, forcing any navigable graph to have many edges.

On the Role of Edge Dependency in Graph Generative Models

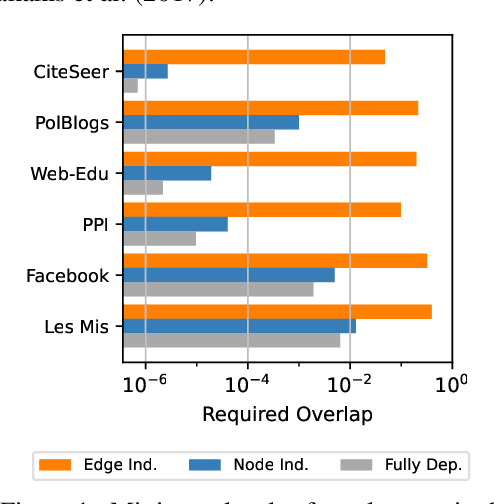
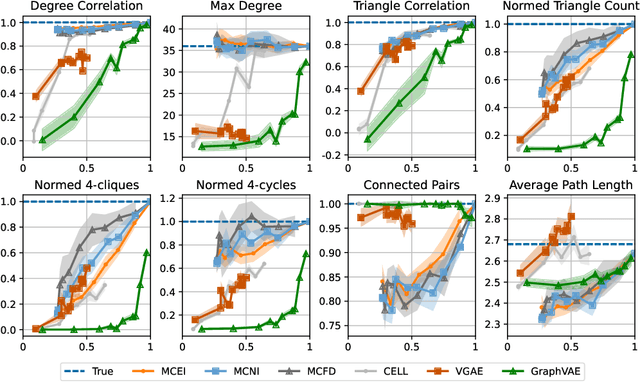
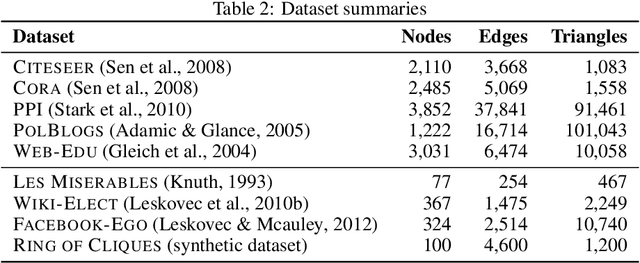
In this work, we introduce a novel evaluation framework for generative models of graphs, emphasizing the importance of model-generated graph overlap (Chanpuriya et al., 2021) to ensure both accuracy and edge-diversity. We delineate a hierarchy of graph generative models categorized into three levels of complexity: edge independent, node independent, and fully dependent models. This hierarchy encapsulates a wide range of prevalent methods. We derive theoretical bounds on the number of triangles and other short-length cycles producible by each level of the hierarchy, contingent on the model overlap. We provide instances demonstrating the asymptotic optimality of our bounds. Furthermore, we introduce new generative models for each of the three hierarchical levels, leveraging dense subgraph discovery (Gionis & Tsourakakis, 2015). Our evaluation, conducted on real-world datasets, focuses on assessing the output quality and overlap of our proposed models in comparison to other popular models. Our results indicate that our simple, interpretable models provide competitive baselines to popular generative models. Through this investigation, we aim to propel the advancement of graph generative models by offering a structured framework and robust evaluation metrics, thereby facilitating the development of models capable of generating accurate and edge-diverse graphs.

Latent Random Steps as Relaxations of Max-Cut, Min-Cut, and More

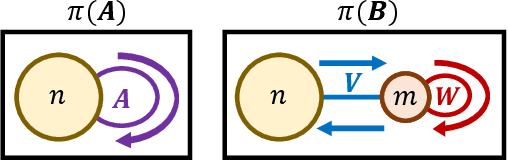
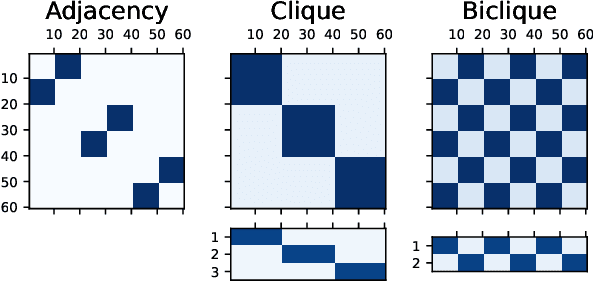
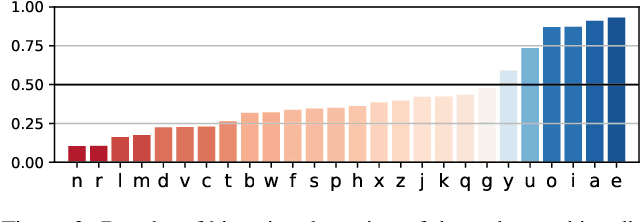
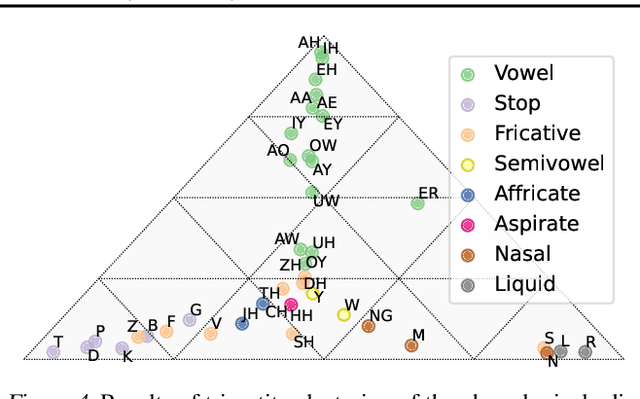
Algorithms for node clustering typically focus on finding homophilous structure in graphs. That is, they find sets of similar nodes with many edges within, rather than across, the clusters. However, graphs often also exhibit heterophilous structure, as exemplified by (nearly) bipartite and tripartite graphs, where most edges occur across the clusters. Grappling with such structure is typically left to the task of graph simplification. We present a probabilistic model based on non-negative matrix factorization which unifies clustering and simplification, and provides a framework for modeling arbitrary graph structure. Our model is based on factorizing the process of taking a random walk on the graph. It permits an unconstrained parametrization, allowing for optimization via simple gradient descent. By relaxing the hard clustering to a soft clustering, our algorithm relaxes potentially hard clustering problems to a tractable ones. We illustrate our algorithm's capabilities on a synthetic graph, as well as simple unsupervised learning tasks involving bipartite and tripartite clustering of orthographic and phonological data.

Kernel Interpolation with Sparse Grids

Structured kernel interpolation (SKI) accelerates Gaussian process (GP) inference by interpolating the kernel covariance function using a dense grid of inducing points, whose corresponding kernel matrix is highly structured and thus amenable to fast linear algebra. Unfortunately, SKI scales poorly in the dimension of the input points, since the dense grid size grows exponentially with the dimension. To mitigate this issue, we propose the use of sparse grids within the SKI framework. These grids enable accurate interpolation, but with a number of points growing more slowly with dimension. We contribute a novel nearly linear time matrix-vector multiplication algorithm for the sparse grid kernel matrix. Next, we describe how sparse grids can be combined with an efficient interpolation scheme based on simplices. With these changes, we demonstrate that SKI can be scaled to higher dimensions while maintaining accuracy.

Optimal Sketching Bounds for Sparse Linear Regression

We study oblivious sketching for $k$-sparse linear regression under various loss functions such as an $\ell_p$ norm, or from a broad class of hinge-like loss functions, which includes the logistic and ReLU losses. We show that for sparse $\ell_2$ norm regression, there is a distribution over oblivious sketches with $\Theta(k\log(d/k)/\varepsilon^2)$ rows, which is tight up to a constant factor. This extends to $\ell_p$ loss with an additional additive $O(k\log(k/\varepsilon)/\varepsilon^2)$ term in the upper bound. This establishes a surprising separation from the related sparse recovery problem, which is an important special case of sparse regression. For this problem, under the $\ell_2$ norm, we observe an upper bound of $O(k \log (d)/\varepsilon + k\log(k/\varepsilon)/\varepsilon^2)$ rows, showing that sparse recovery is strictly easier to sketch than sparse regression. For sparse regression under hinge-like loss functions including sparse logistic and sparse ReLU regression, we give the first known sketching bounds that achieve $o(d)$ rows showing that $O(\mu^2 k\log(\mu n d/\varepsilon)/\varepsilon^2)$ rows suffice, where $\mu$ is a natural complexity parameter needed to obtain relative error bounds for these loss functions. We again show that this dimension is tight, up to lower order terms and the dependence on $\mu$. Finally, we show that similar sketching bounds can be achieved for LASSO regression, a popular convex relaxation of sparse regression, where one aims to minimize $\|Ax-b\|_2^2+\lambda\|x\|_1$ over $x\in\mathbb{R}^d$. We show that sketching dimension $O(\log(d)/(\lambda \varepsilon)^2)$ suffices and that the dependence on $d$ and $\lambda$ is tight.

No-regret Algorithms for Fair Resource Allocation

We consider a fair resource allocation problem in the no-regret setting against an unrestricted adversary. The objective is to allocate resources equitably among several agents in an online fashion so that the difference of the aggregate $\alpha$-fair utilities of the agents between an optimal static clairvoyant allocation and that of the online policy grows sub-linearly with time. The problem is challenging due to the non-additive nature of the $\alpha$-fairness function. Previously, it was shown that no online policy can exist for this problem with a sublinear standard regret. In this paper, we propose an efficient online resource allocation policy, called Online Proportional Fair (OPF), that achieves $c_\alpha$-approximate sublinear regret with the approximation factor $c_\alpha=(1-\alpha)^{-(1-\alpha)}\leq 1.445,$ for $0\leq \alpha < 1$. The upper bound to the $c_\alpha$-regret for this problem exhibits a surprising phase transition phenomenon. The regret bound changes from a power-law to a constant at the critical exponent $\alpha=\frac{1}{2}.$ As a corollary, our result also resolves an open problem raised by Even-Dar et al. [2009] on designing an efficient no-regret policy for the online job scheduling problem in certain parameter regimes. The proof of our results introduces new algorithmic and analytical techniques, including greedy estimation of the future gradients for non-additive global reward functions and bootstrapping adaptive regret bounds, which may be of independent interest.