On the Role of Edge Dependency in Graph Generative Models

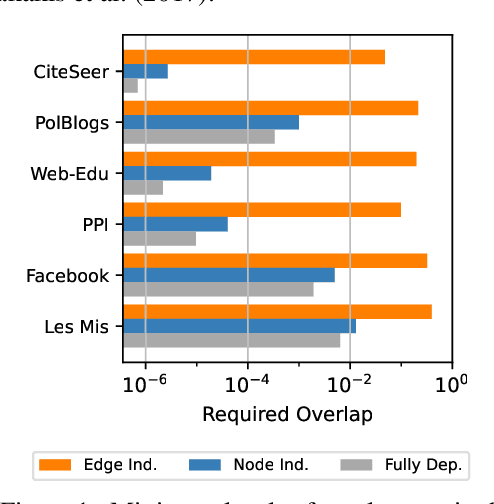
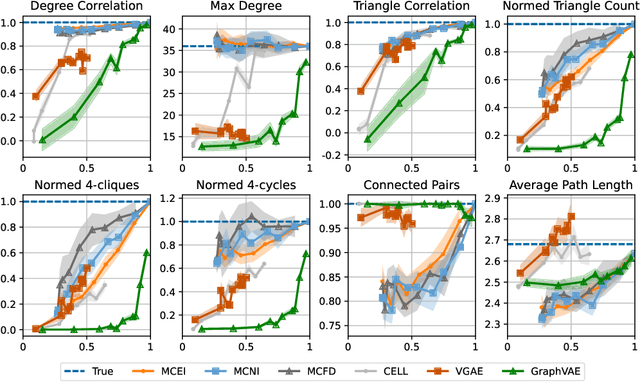
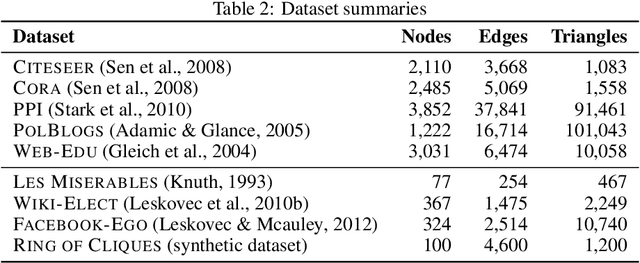
In this work, we introduce a novel evaluation framework for generative models of graphs, emphasizing the importance of model-generated graph overlap (Chanpuriya et al., 2021) to ensure both accuracy and edge-diversity. We delineate a hierarchy of graph generative models categorized into three levels of complexity: edge independent, node independent, and fully dependent models. This hierarchy encapsulates a wide range of prevalent methods. We derive theoretical bounds on the number of triangles and other short-length cycles producible by each level of the hierarchy, contingent on the model overlap. We provide instances demonstrating the asymptotic optimality of our bounds. Furthermore, we introduce new generative models for each of the three hierarchical levels, leveraging dense subgraph discovery (Gionis & Tsourakakis, 2015). Our evaluation, conducted on real-world datasets, focuses on assessing the output quality and overlap of our proposed models in comparison to other popular models. Our results indicate that our simple, interpretable models provide competitive baselines to popular generative models. Through this investigation, we aim to propel the advancement of graph generative models by offering a structured framework and robust evaluation metrics, thereby facilitating the development of models capable of generating accurate and edge-diverse graphs.

Query-Efficient Correlation Clustering

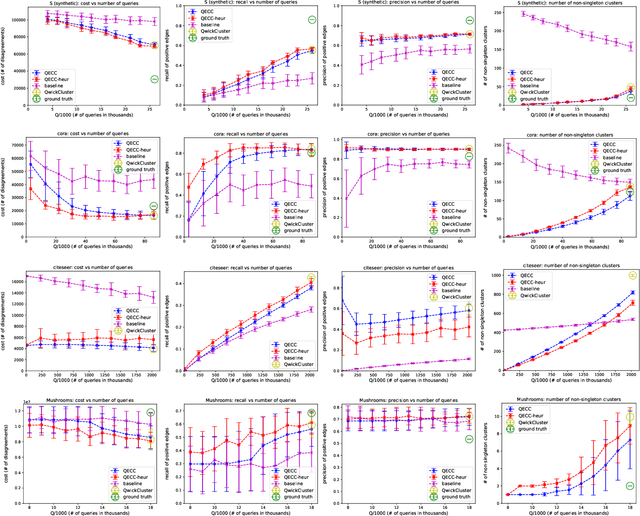
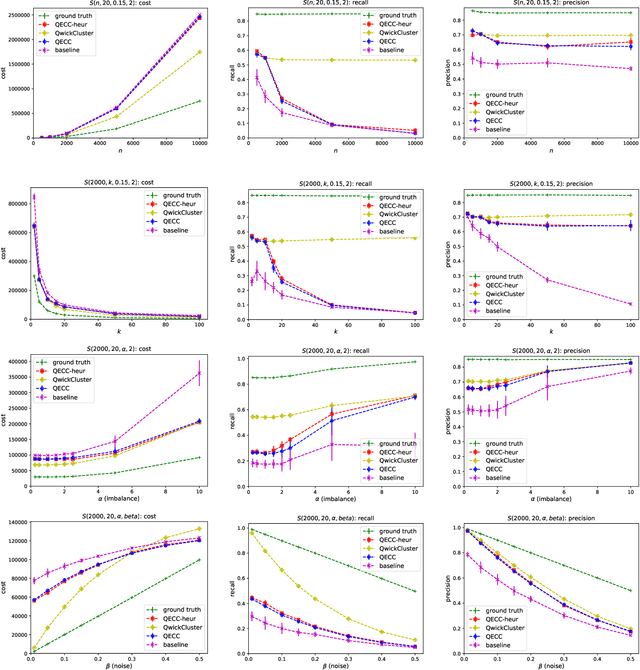
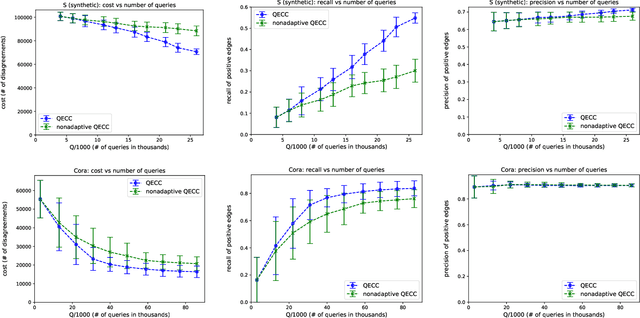
Correlation clustering is arguably the most natural formulation of clustering. Given n objects and a pairwise similarity measure, the goal is to cluster the objects so that, to the best possible extent, similar objects are put in the same cluster and dissimilar objects are put in different clusters. A main drawback of correlation clustering is that it requires as input the $\Theta(n^2)$ pairwise similarities. This is often infeasible to compute or even just to store. In this paper we study \emph{query-efficient} algorithms for correlation clustering. Specifically, we devise a correlation clustering algorithm that, given a budget of $Q$ queries, attains a solution whose expected number of disagreements is at most $3\cdot OPT + O(\frac{n^3}{Q})$, where $OPT$ is the optimal cost for the instance. Its running time is $O(Q)$, and can be easily made non-adaptive (meaning it can specify all its queries at the outset and make them in parallel) with the same guarantees. Up to constant factors, our algorithm yields a provably optimal trade-off between the number of queries $Q$ and the worst-case error attained, even for adaptive algorithms. Finally, we perform an experimental study of our proposed method on both synthetic and real data, showing the scalability and the accuracy of our algorithm.