ULTRA-MC: A Unified Approach to Learning Mixtures of Markov Chains via Hitting Times

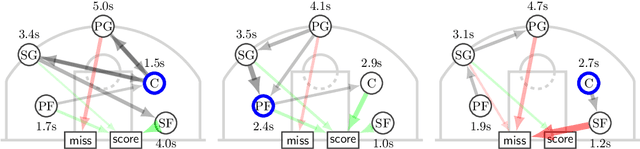
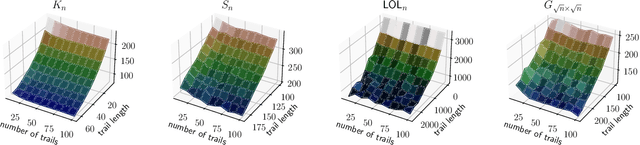
This study introduces a novel approach for learning mixtures of Markov chains, a critical process applicable to various fields, including healthcare and the analysis of web users. Existing research has identified a clear divide in methodologies for learning mixtures of discrete and continuous-time Markov chains, while the latter presents additional complexities for recovery accuracy and efficiency. We introduce a unifying strategy for learning mixtures of discrete and continuous-time Markov chains, focusing on hitting times, which are well defined for both types. Specifically, we design a reconstruction algorithm that outputs a mixture which accurately reflects the estimated hitting times and demonstrates resilience to noise. We introduce an efficient gradient-descent approach, specifically tailored to manage the computational complexity and non-symmetric characteristics inherent in the calculation of hitting time derivatives. Our approach is also of significant interest when applied to a single Markov chain, thus extending the methodologies previously established by Hoskins et al. and Wittmann et al. We complement our theoretical work with experiments conducted on synthetic and real-world datasets, providing a comprehensive evaluation of our methodology.

On the Role of Edge Dependency in Graph Generative Models

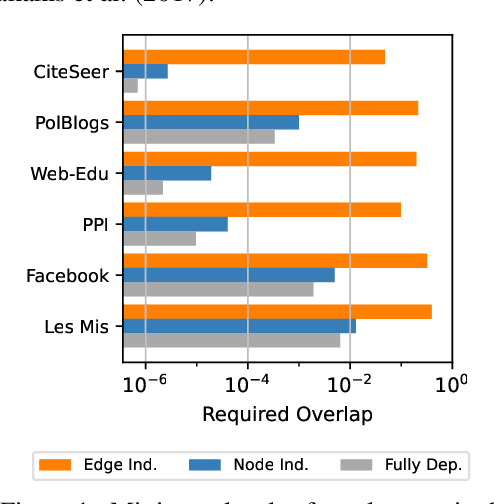
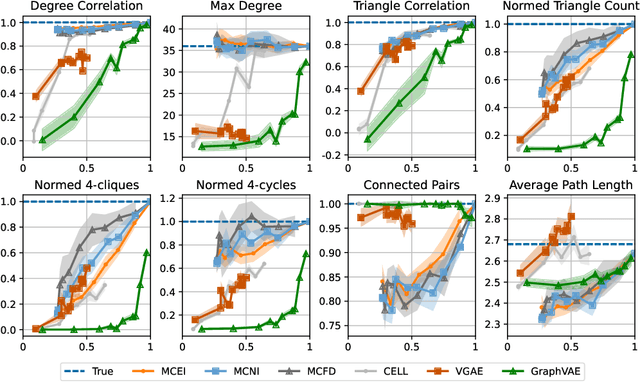
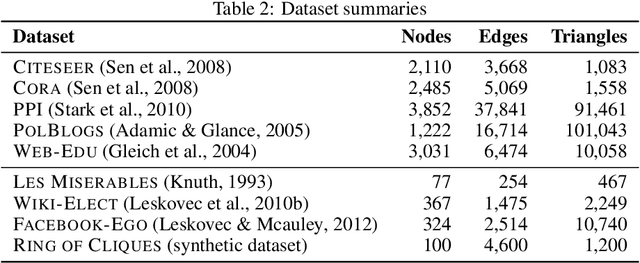
In this work, we introduce a novel evaluation framework for generative models of graphs, emphasizing the importance of model-generated graph overlap (Chanpuriya et al., 2021) to ensure both accuracy and edge-diversity. We delineate a hierarchy of graph generative models categorized into three levels of complexity: edge independent, node independent, and fully dependent models. This hierarchy encapsulates a wide range of prevalent methods. We derive theoretical bounds on the number of triangles and other short-length cycles producible by each level of the hierarchy, contingent on the model overlap. We provide instances demonstrating the asymptotic optimality of our bounds. Furthermore, we introduce new generative models for each of the three hierarchical levels, leveraging dense subgraph discovery (Gionis & Tsourakakis, 2015). Our evaluation, conducted on real-world datasets, focuses on assessing the output quality and overlap of our proposed models in comparison to other popular models. Our results indicate that our simple, interpretable models provide competitive baselines to popular generative models. Through this investigation, we aim to propel the advancement of graph generative models by offering a structured framework and robust evaluation metrics, thereby facilitating the development of models capable of generating accurate and edge-diverse graphs.

ADAMM: Anomaly Detection of Attributed Multi-graphs with Metadata: A Unified Neural Network Approach

Given a complex graph database of node- and edge-attributed multi-graphs as well as associated metadata for each graph, how can we spot the anomalous instances? Many real-world problems can be cast as graph inference tasks where the graph representation could capture complex relational phenomena (e.g., transactions among financial accounts in a journal entry), along with metadata reflecting tabular features (e.g. approver, effective date, etc.). While numerous anomaly detectors based on Graph Neural Networks (GNNs) have been proposed, none are capable of directly handling directed graphs with multi-edges and self-loops. Furthermore, the simultaneous handling of relational and tabular features remains an unexplored area. In this work we propose ADAMM, a novel graph neural network model that handles directed multi-graphs, providing a unified end-to-end architecture that fuses metadata and graph-level representation learning through an unsupervised anomaly detection objective. Experiments on datasets from two different domains, namely, general-ledger journal entries from different firms (accounting) as well as human GPS trajectories from thousands of individuals (urban mobility) validate ADAMM's generality and detection effectiveness of expert-guided and ground-truth anomalies. Notably, ADAMM outperforms existing baselines that handle the two data modalities (graph and metadata) separately with post hoc synthesis efforts.

On the Power of Edge Independent Graph Models

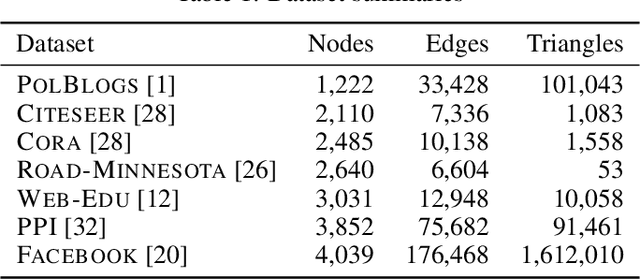
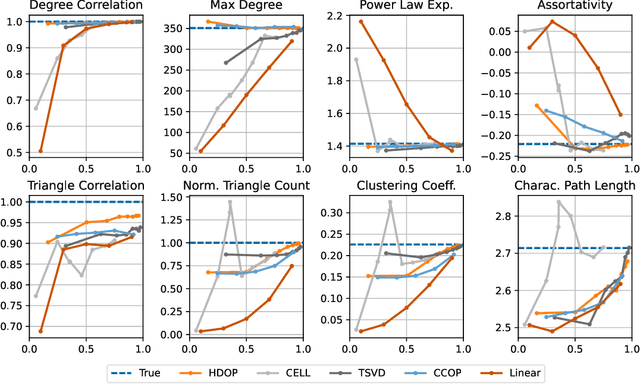
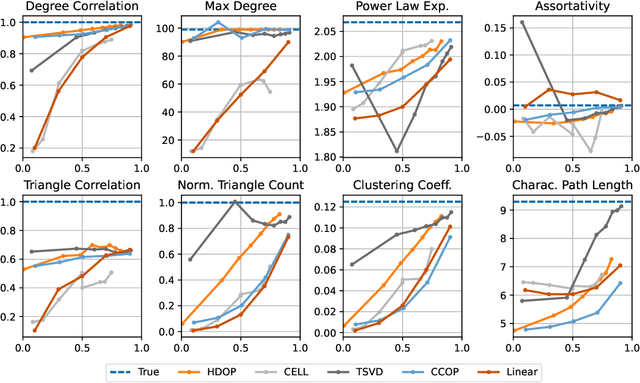
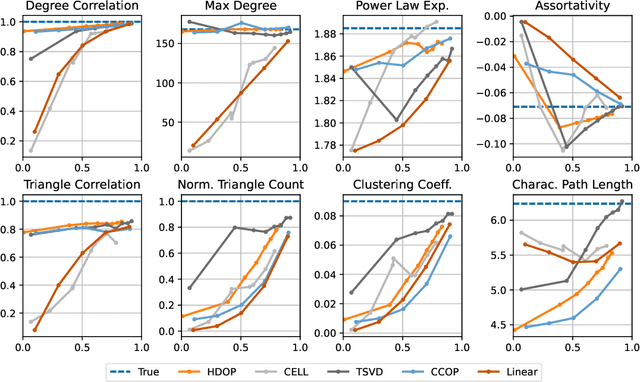
Why do many modern neural-network-based graph generative models fail to reproduce typical real-world network characteristics, such as high triangle density? In this work we study the limitations of edge independent random graph models, in which each edge is added to the graph independently with some probability. Such models include both the classic Erd\"{o}s-R\'{e}nyi and stochastic block models, as well as modern generative models such as NetGAN, variational graph autoencoders, and CELL. We prove that subject to a bounded overlap condition, which ensures that the model does not simply memorize a single graph, edge independent models are inherently limited in their ability to generate graphs with high triangle and other subgraph densities. Notably, such high densities are known to appear in real-world social networks and other graphs. We complement our negative results with a simple generative model that balances overlap and accuracy, performing comparably to more complex models in reconstructing many graph statistics.

DeepWalking Backwards: From Embeddings Back to Graphs

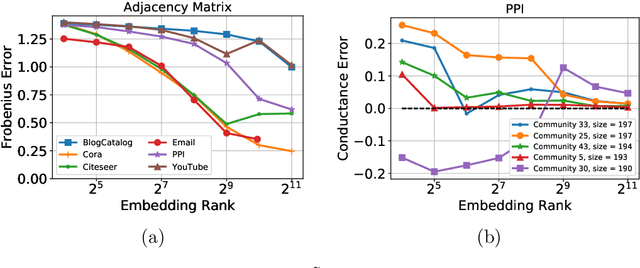
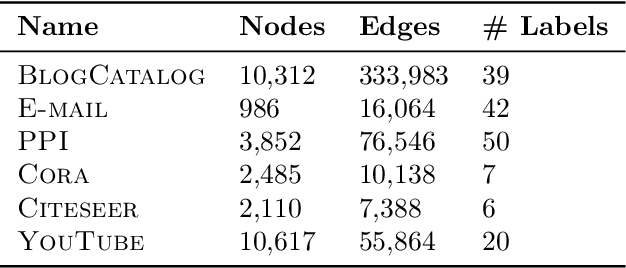
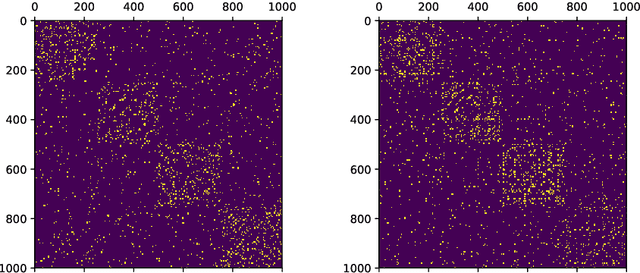
Low-dimensional node embeddings play a key role in analyzing graph datasets. However, little work studies exactly what information is encoded by popular embedding methods, and how this information correlates with performance in downstream machine learning tasks. We tackle this question by studying whether embeddings can be inverted to (approximately) recover the graph used to generate them. Focusing on a variant of the popular DeepWalk method (Perozzi et al., 2014; Qiu et al., 2018), we present algorithms for accurate embedding inversion - i.e., from the low-dimensional embedding of a graph G, we can find a graph H with a very similar embedding. We perform numerous experiments on real-world networks, observing that significant information about G, such as specific edges and bulk properties like triangle density, is often lost in H. However, community structure is often preserved or even enhanced. Our findings are a step towards a more rigorous understanding of exactly what information embeddings encode about the input graph, and why this information is useful for learning tasks.

Node Embeddings and Exact Low-Rank Representations of Complex Networks

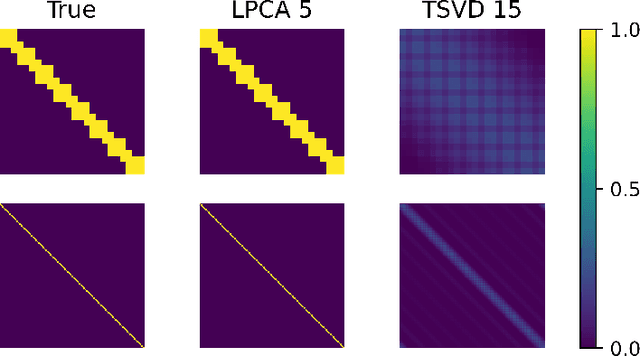
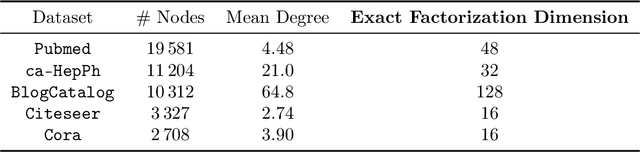
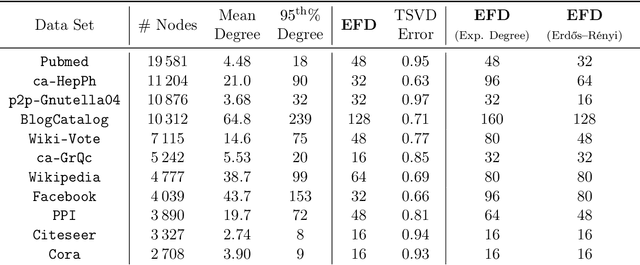
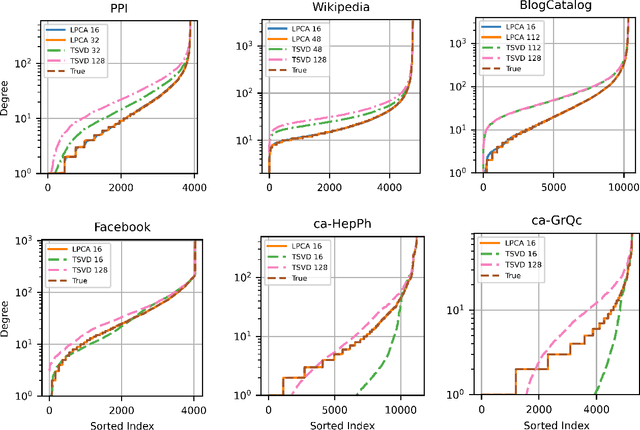
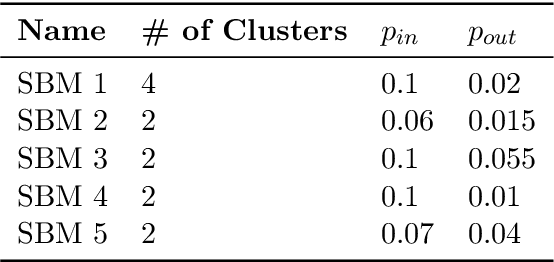
Low-dimensional embeddings, from classical spectral embeddings to modern neural-net-inspired methods, are a cornerstone in the modeling and analysis of complex networks. Recent work by Seshadhri et al. (PNAS 2020) suggests that such embeddings cannot capture local structure arising in complex networks. In particular, they show that any network generated from a natural low-dimensional model cannot be both sparse and have high triangle density (high clustering coefficient), two hallmark properties of many real-world networks. In this work we show that the results of Seshadhri et al. are intimately connected to the model they use rather than the low-dimensional structure of complex networks. Specifically, we prove that a minor relaxation of their model can generate sparse graphs with high triangle density. Surprisingly, we show that this same model leads to exact low-dimensional factorizations of many real-world networks. We give a simple algorithm based on logistic principal component analysis (LPCA) that succeeds in finding such exact embeddings. Finally, we perform a large number of experiments that verify the ability of very low-dimensional embeddings to capture local structure in real-world networks.

TwitterMancer: Predicting Interactions on Twitter Accurately

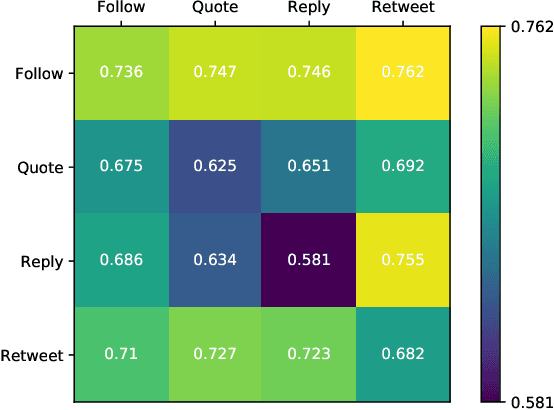
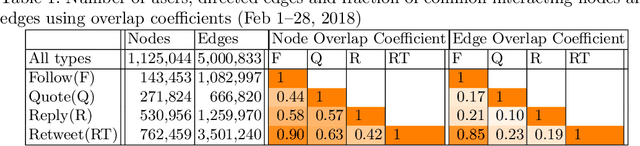
This paper investigates the interplay between different types of user interactions on Twitter, with respect to predicting missing or unseen interactions. For example, given a set of retweet interactions between Twitter users, how accurately can we predict reply interactions? Is it more difficult to predict retweet or quote interactions between a pair of accounts? Also, how important is time locality, and which features of interaction patterns are most important to enable accurate prediction of specific Twitter interactions? Our empirical study of Twitter interactions contributes initial answers to these questions. We have crawled an extensive dataset of Greek-speaking Twitter accounts and their follow, quote, retweet, reply interactions over a period of a month. We find we can accurately predict many interactions of Twitter users. Interestingly, the most predictive features vary with the user profiles, and are not the same across all users. For example, for a pair of users that interact with a large number of other Twitter users, we find that certain "higher-dimensional" triads, i.e., triads that involve multiple types of interactions, are very informative, whereas for less active Twitter users, certain in-degrees and out-degrees play a major role. Finally, we provide various other insights on Twitter user behavior. Our code and data are available at https://github.com/twittermancer/. Keywords: Graph mining, machine learning, social media, social networks