ULTRA-MC: A Unified Approach to Learning Mixtures of Markov Chains via Hitting Times
Paper and Code
May 23, 2024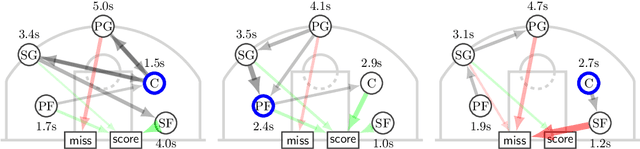

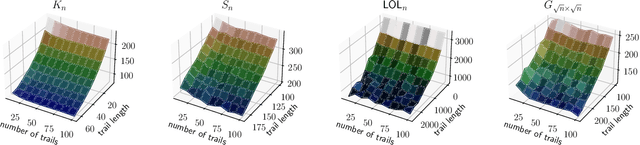

This study introduces a novel approach for learning mixtures of Markov chains, a critical process applicable to various fields, including healthcare and the analysis of web users. Existing research has identified a clear divide in methodologies for learning mixtures of discrete and continuous-time Markov chains, while the latter presents additional complexities for recovery accuracy and efficiency. We introduce a unifying strategy for learning mixtures of discrete and continuous-time Markov chains, focusing on hitting times, which are well defined for both types. Specifically, we design a reconstruction algorithm that outputs a mixture which accurately reflects the estimated hitting times and demonstrates resilience to noise. We introduce an efficient gradient-descent approach, specifically tailored to manage the computational complexity and non-symmetric characteristics inherent in the calculation of hitting time derivatives. Our approach is also of significant interest when applied to a single Markov chain, thus extending the methodologies previously established by Hoskins et al. and Wittmann et al. We complement our theoretical work with experiments conducted on synthetic and real-world datasets, providing a comprehensive evaluation of our methodology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge