ULTRA-MC: A Unified Approach to Learning Mixtures of Markov Chains via Hitting Times

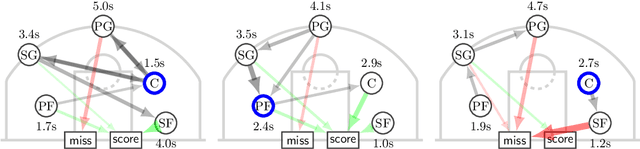
This study introduces a novel approach for learning mixtures of Markov chains, a critical process applicable to various fields, including healthcare and the analysis of web users. Existing research has identified a clear divide in methodologies for learning mixtures of discrete and continuous-time Markov chains, while the latter presents additional complexities for recovery accuracy and efficiency. We introduce a unifying strategy for learning mixtures of discrete and continuous-time Markov chains, focusing on hitting times, which are well defined for both types. Specifically, we design a reconstruction algorithm that outputs a mixture which accurately reflects the estimated hitting times and demonstrates resilience to noise. We introduce an efficient gradient-descent approach, specifically tailored to manage the computational complexity and non-symmetric characteristics inherent in the calculation of hitting time derivatives. Our approach is also of significant interest when applied to a single Markov chain, thus extending the methodologies previously established by Hoskins et al. and Wittmann et al. We complement our theoretical work with experiments conducted on synthetic and real-world datasets, providing a comprehensive evaluation of our methodology.

Markovletics: Methods and A Novel Application for Learning Continuous-Time Markov Chain Mixtures

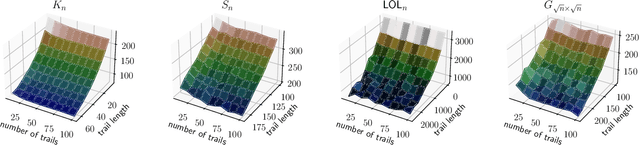
Sequential data naturally arises from user engagement on digital platforms like social media, music streaming services, and web navigation, encapsulating evolving user preferences and behaviors through continuous information streams. A notable unresolved query in stochastic processes is learning mixtures of continuous-time Markov chains (CTMCs). While there is progress in learning mixtures of discrete-time Markov chains with recovery guarantees [GKV16,ST23,KTT2023], the continuous scenario uncovers unique unexplored challenges. The intrigue in CTMC mixtures stems from their potential to model intricate continuous-time stochastic processes prevalent in various fields including social media, finance, and biology. In this study, we introduce a novel framework for exploring CTMCs, emphasizing the influence of observed trails' length and mixture parameters on problem regimes, which demands specific algorithms. Through thorough experimentation, we examine the impact of discretizing continuous-time trails on the learnability of the continuous-time mixture, given that these processes are often observed via discrete, resource-demanding observations. Our comparative analysis with leading methods explores sample complexity and the trade-off between the number of trails and their lengths, offering crucial insights for method selection in different problem instances. We apply our algorithms on an extensive collection of Lastfm's user-generated trails spanning three years, demonstrating the capability of our algorithms to differentiate diverse user preferences. We pioneer the use of CTMC mixtures on a basketball passing dataset to unveil intricate offensive tactics of NBA teams. This underscores the pragmatic utility and versatility of our proposed framework. All results presented in this study are replicable, and we provide the implementations to facilitate reproducibility.

Online and Streaming Algorithms for Constrained $k$-Submodular Maximization

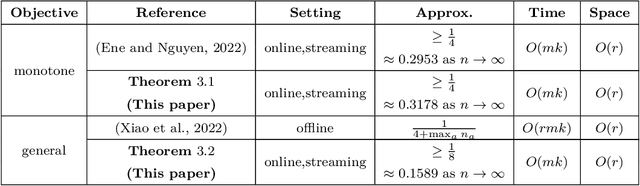
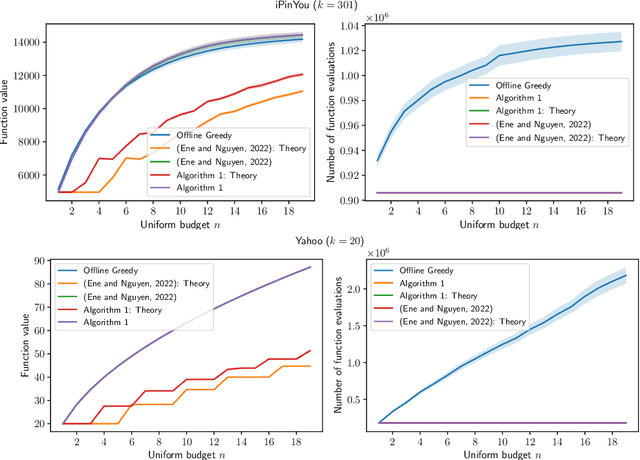
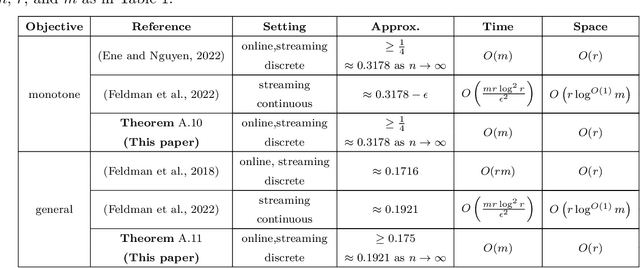
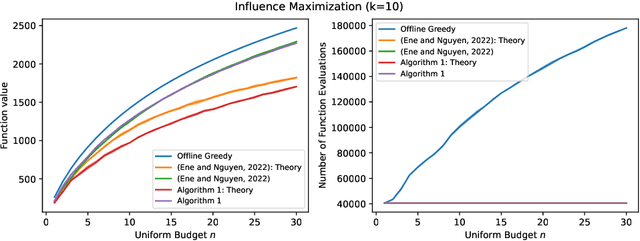
Constrained $k$-submodular maximization is a general framework that captures many discrete optimization problems such as ad allocation, influence maximization, personalized recommendation, and many others. In many of these applications, datasets are large or decisions need to be made in an online manner, which motivates the development of efficient streaming and online algorithms. In this work, we develop single-pass streaming and online algorithms for constrained $k$-submodular maximization with both monotone and general (possibly non-monotone) objectives subject to cardinality and knapsack constraints. Our algorithms achieve provable constant-factor approximation guarantees which improve upon the state of the art in almost all settings. Moreover, they are combinatorial and very efficient, and have optimal space and running time. We experimentally evaluate our algorithms on instances for ad allocation and other applications, where we observe that our algorithms are efficient and scalable, and construct solutions that are comparable in value to offline greedy algorithms.

Learning Mixtures of Markov Chains with Quality Guarantees

A large number of modern applications ranging from listening songs online and browsing the Web to using a navigation app on a smartphone generate a plethora of user trails. Clustering such trails into groups with a common sequence pattern can reveal significant structure in human behavior that can lead to improving user experience through better recommendations, and even prevent suicides [LMCR14]. One approach to modeling this problem mathematically is as a mixture of Markov chains. Recently, Gupta, Kumar and Vassilvitski [GKV16] introduced an algorithm (GKV-SVD) based on the singular value decomposition (SVD) that under certain conditions can perfectly recover a mixture of L chains on n states, given only the distribution of trails of length 3 (3-trail). In this work we contribute to the problem of unmixing Markov chains by highlighting and addressing two important constraints of the GKV-SVD algorithm [GKV16]: some chains in the mixture may not even be weakly connected, and secondly in practice one does not know beforehand the true number of chains. We resolve these issues in the Gupta et al. paper [GKV16]. Specifically, we propose an algebraic criterion that enables us to choose a value of L efficiently that avoids overfitting. Furthermore, we design a reconstruction algorithm that outputs the true mixture in the presence of disconnected chains and is robust to noise. We complement our theoretical results with experiments on both synthetic and real data, where we observe that our method outperforms the GKV-SVD algorithm. Finally, we empirically observe that combining an EM-algorithm with our method performs best in practice, both in terms of reconstruction error with respect to the distribution of 3-trails and the mixture of Markov Chains.

Online Ad Allocation with Predictions

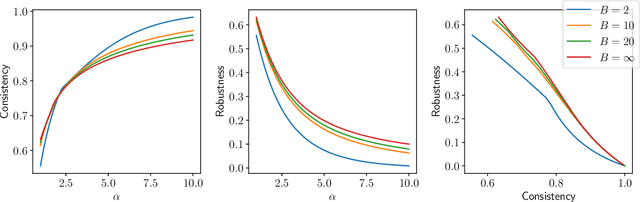
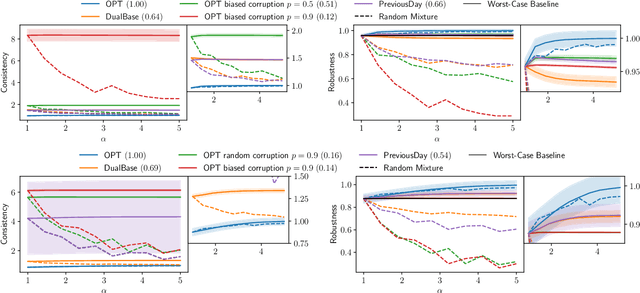
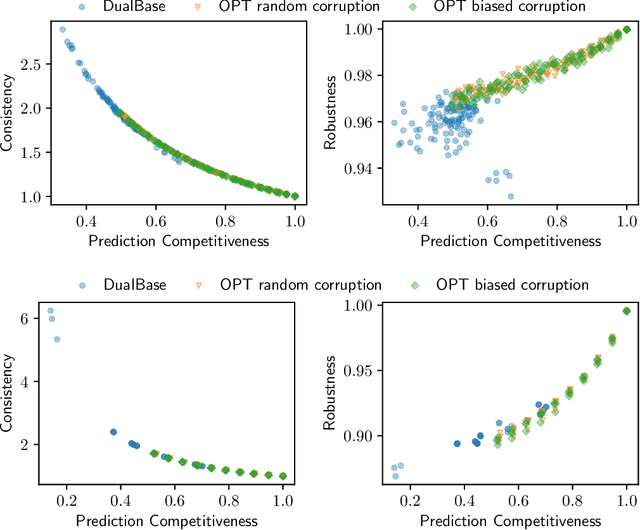
Display Ads and the generalized assignment problem are two well-studied online packing problems with important applications in ad allocation and other areas. In both problems, ad impressions arrive online and have to be allocated immediately to budget-constrained advertisers. Worst-case algorithms that achieve the ideal competitive ratio are known, but might act overly conservative given the predictable and usually tame nature of real-world input. Given this discrepancy, we develop an algorithm for both problems that incorporate machine-learned predictions and can thus improve the performance beyond the worst-case. Our algorithm is based on the work of Feldman et al. (2009) and similar in nature to Mahdian et al. (2007) who were the first to develop a learning-augmented algorithm for the related, but more structured Ad Words problem. We use a novel analysis to show that our algorithm is able to capitalize on a good prediction, while being robust against poor predictions. We experimentally evaluate our algorithm on synthetic and real-world data on a wide range of predictions. Our algorithm is consistently outperforming the worst-case algorithm without predictions.

Global Evaluation for Decision Tree Learning

We transfer distances on clusterings to the building process of decision trees, and as a consequence extend the classical ID3 algorithm to perform modifications based on the global distance of the tree to the ground truth--instead of considering single leaves. Next, we evaluate this idea in comparison with the original version and discuss occurring problems, but also strengths of the global approach. On this basis, we finish by identifying other scenarios where global evaluations are worthwhile.