On the Role of Edge Dependency in Graph Generative Models
Paper and Code
Dec 06, 2023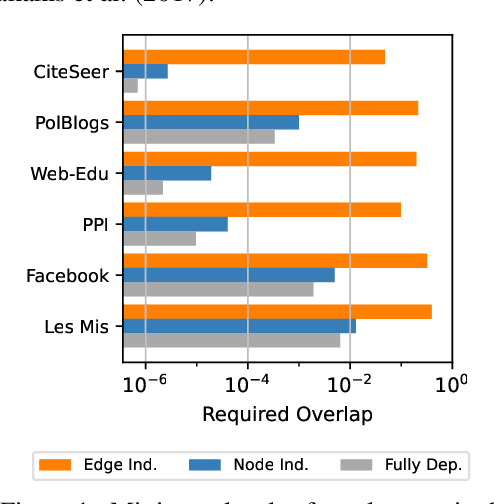

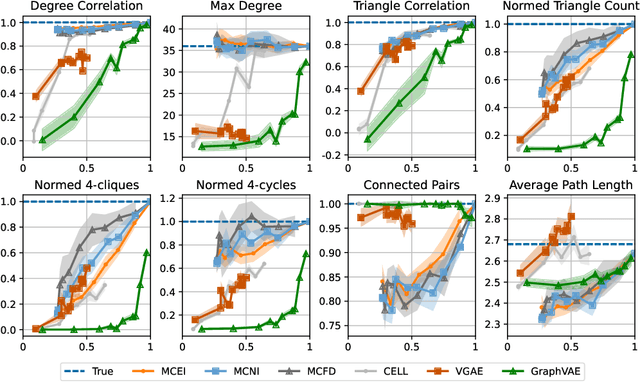
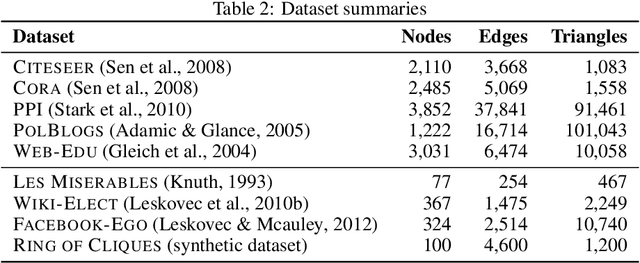
In this work, we introduce a novel evaluation framework for generative models of graphs, emphasizing the importance of model-generated graph overlap (Chanpuriya et al., 2021) to ensure both accuracy and edge-diversity. We delineate a hierarchy of graph generative models categorized into three levels of complexity: edge independent, node independent, and fully dependent models. This hierarchy encapsulates a wide range of prevalent methods. We derive theoretical bounds on the number of triangles and other short-length cycles producible by each level of the hierarchy, contingent on the model overlap. We provide instances demonstrating the asymptotic optimality of our bounds. Furthermore, we introduce new generative models for each of the three hierarchical levels, leveraging dense subgraph discovery (Gionis & Tsourakakis, 2015). Our evaluation, conducted on real-world datasets, focuses on assessing the output quality and overlap of our proposed models in comparison to other popular models. Our results indicate that our simple, interpretable models provide competitive baselines to popular generative models. Through this investigation, we aim to propel the advancement of graph generative models by offering a structured framework and robust evaluation metrics, thereby facilitating the development of models capable of generating accurate and edge-diverse graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge