LoNe Sampler: Graph node embeddings by coordinated local neighborhood sampling

Local graph neighborhood sampling is a fundamental computational problem that is at the heart of algorithms for node representation learning. Several works have presented algorithms for learning discrete node embeddings where graph nodes are represented by discrete features such as attributes of neighborhood nodes. Discrete embeddings offer several advantages compared to continuous word2vec-like node embeddings: ease of computation, scalability, and interpretability. We present LoNe Sampler, a suite of algorithms for generating discrete node embeddings by Local Neighborhood Sampling, and address two shortcomings of previous work. First, our algorithms have rigorously understood theoretical properties. Second, we show how to generate approximate explicit vector maps that avoid the expensive computation of a Gram matrix for the training of a kernel model. Experiments on benchmark datasets confirm the theoretical findings and demonstrate the advantages of the proposed methods.

COLOGNE: Coordinated Local Graph Neighborhood Sampling

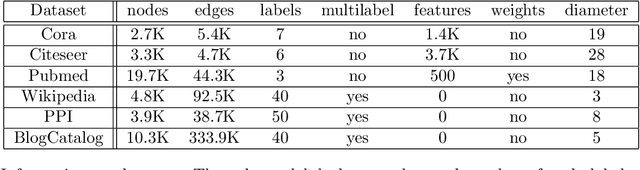
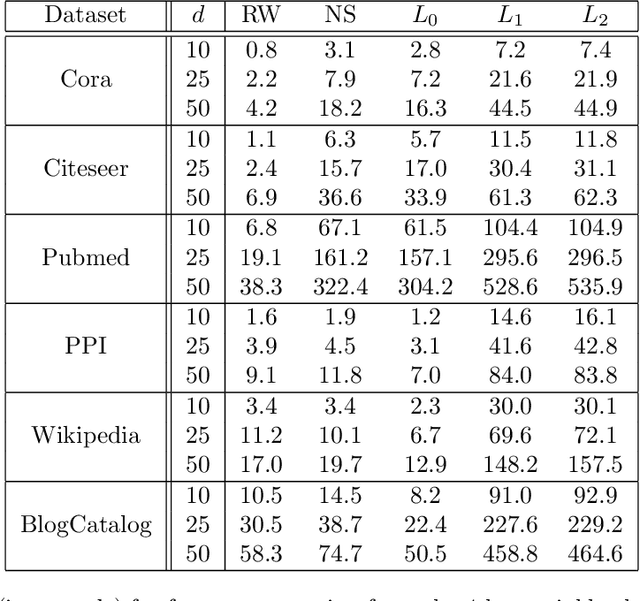
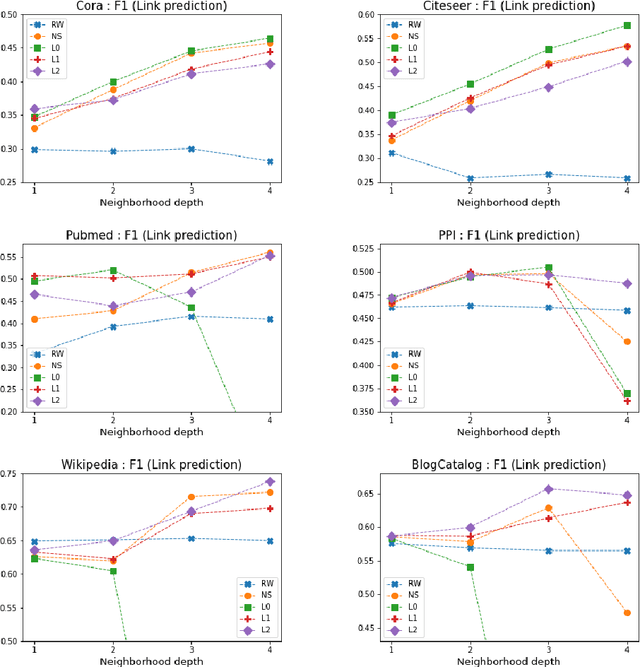
Representation learning for graphs enables the application of standard machine learning algorithms and data analysis tools to graph data. Replacing discrete unordered objects such as graph nodes by real-valued vectors is at the heart of many approaches to learning from graph data. Such vector representations, or embeddings, capture the discrete relationships in the original data by representing nodes as vectors in a high-dimensional space. In most applications graphs model the relationship between real-life objects and often nodes contain valuable meta-information about the original objects. While being a powerful machine learning tool, embeddings are not able to preserve such node attributes. We address this shortcoming and consider the problem of learning discrete node embeddings such that the coordinates of the node vector representations are graph nodes. This opens the door to designing interpretable machine learning algorithms for graphs as all attributes originally present in the nodes are preserved. We present a framework for coordinated local graph neighborhood sampling (COLOGNE) such that each node is represented by a fixed number of graph nodes, together with their attributes. Individual samples are coordinated and they preserve the similarity between node neighborhoods. We consider different notions of similarity for which we design scalable algorithms. We show theoretical results for all proposed algorithms. Experiments on benchmark graphs evaluate the quality of the designed embeddings and demonstrate how the proposed embeddings can be used in training interpretable machine learning algorithms for graph data.

Query-Efficient Correlation Clustering

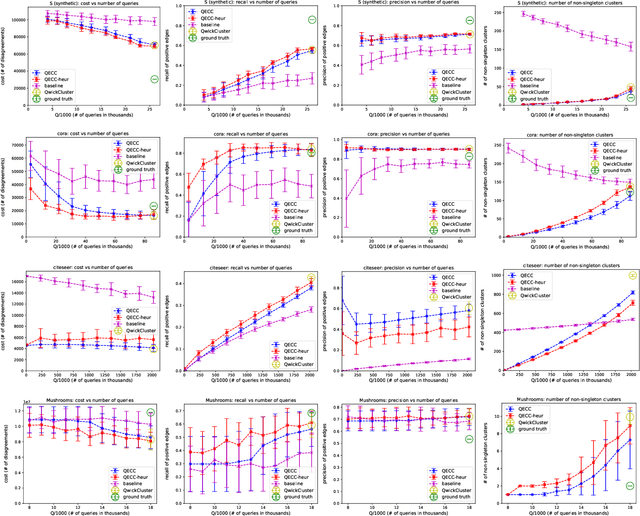
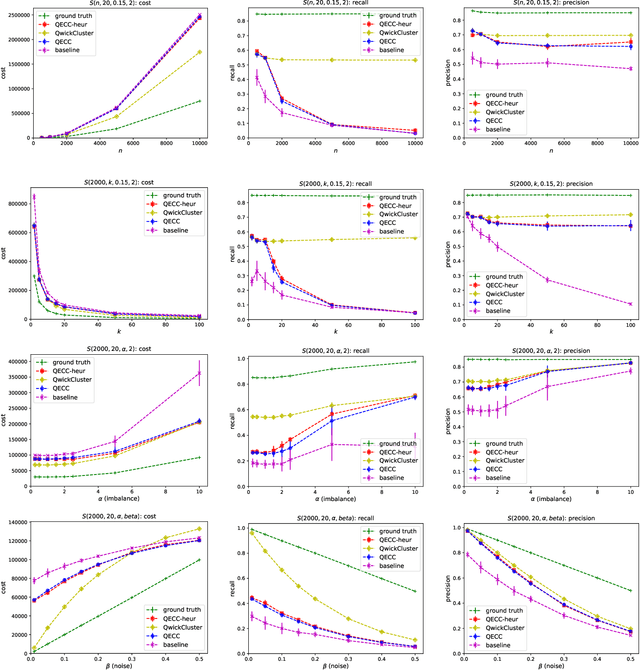
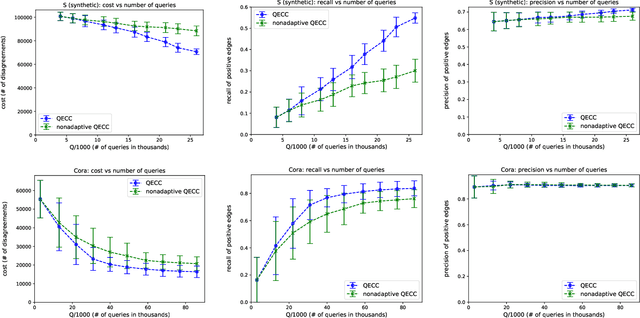
Correlation clustering is arguably the most natural formulation of clustering. Given n objects and a pairwise similarity measure, the goal is to cluster the objects so that, to the best possible extent, similar objects are put in the same cluster and dissimilar objects are put in different clusters. A main drawback of correlation clustering is that it requires as input the $\Theta(n^2)$ pairwise similarities. This is often infeasible to compute or even just to store. In this paper we study \emph{query-efficient} algorithms for correlation clustering. Specifically, we devise a correlation clustering algorithm that, given a budget of $Q$ queries, attains a solution whose expected number of disagreements is at most $3\cdot OPT + O(\frac{n^3}{Q})$, where $OPT$ is the optimal cost for the instance. Its running time is $O(Q)$, and can be easily made non-adaptive (meaning it can specify all its queries at the outset and make them in parallel) with the same guarantees. Up to constant factors, our algorithm yields a provably optimal trade-off between the number of queries $Q$ and the worst-case error attained, even for adaptive algorithms. Finally, we perform an experimental study of our proposed method on both synthetic and real data, showing the scalability and the accuracy of our algorithm.

KONG: Kernels for ordered-neighborhood graphs

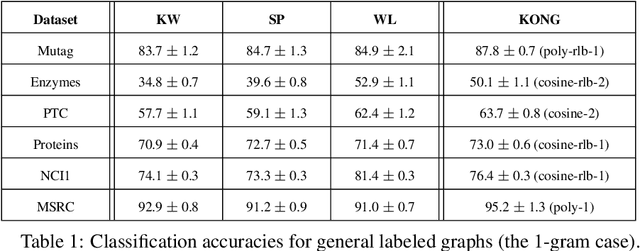
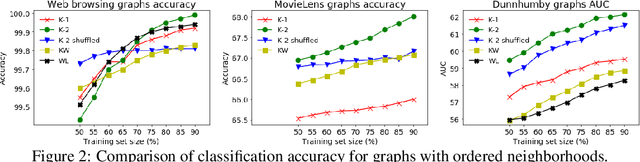
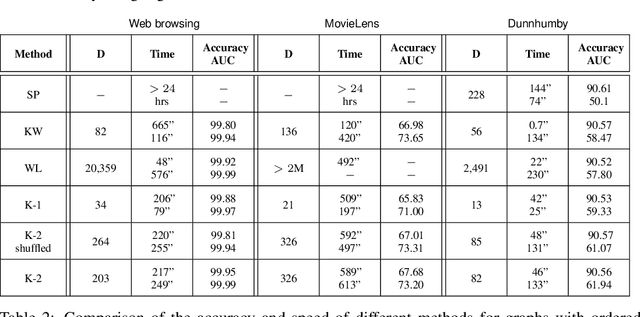
We present novel graph kernels for graphs with node and edge labels that have ordered neighborhoods, i.e. when neighbor nodes follow an order. Graphs with ordered neighborhoods are a natural data representation for evolving graphs where edges are created over time, which induces an order. Combining convolutional subgraph kernels and string kernels, we design new scalable algorithms for generation of explicit graph feature maps using sketching techniques. We obtain precise bounds for the approximation accuracy and computational complexity of the proposed approaches and demonstrate their applicability on real datasets. In particular, our experiments demonstrate that neighborhood ordering results in more informative features. For the special case of general graphs, i.e. graphs without ordered neighborhoods, the new graph kernels yield efficient and simple algorithms for the comparison of label distributions between graphs.

Learning Convolutional Neural Networks for Graphs

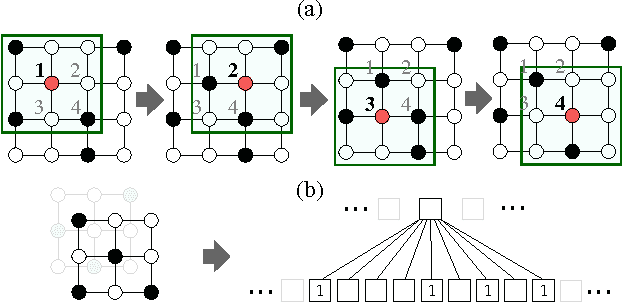
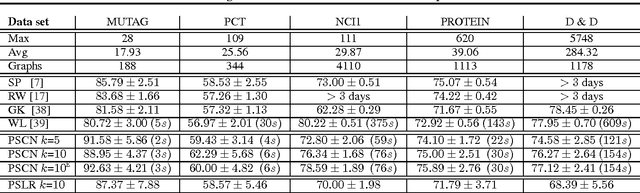
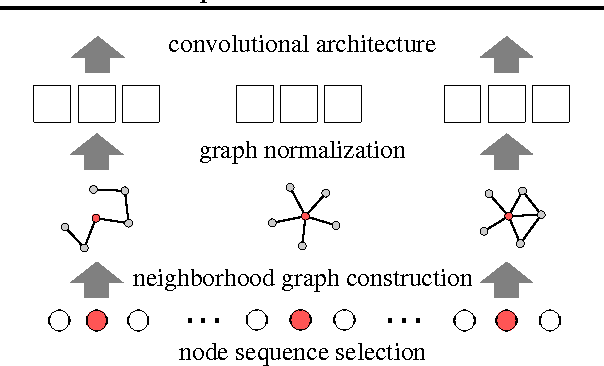
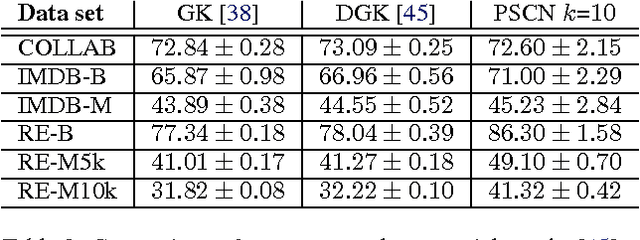
Numerous important problems can be framed as learning from graph data. We propose a framework for learning convolutional neural networks for arbitrary graphs. These graphs may be undirected, directed, and with both discrete and continuous node and edge attributes. Analogous to image-based convolutional networks that operate on locally connected regions of the input, we present a general approach to extracting locally connected regions from graphs. Using established benchmark data sets, we demonstrate that the learned feature representations are competitive with state of the art graph kernels and that their computation is highly efficient.