Rotting Infinitely Many-armed Bandits beyond the Worst-case Rotting: An Adaptive Approach

In this study, we consider the infinitely many armed bandit problems in rotting environments, where the mean reward of an arm may decrease with each pull, while otherwise, it remains unchanged. We explore two scenarios capturing problem-dependent characteristics regarding the decay of rewards: one in which the cumulative amount of rotting is bounded by $V_T$, referred to as the slow-rotting scenario, and the other in which the number of rotting instances is bounded by $S_T$, referred to as the abrupt-rotting scenario. To address the challenge posed by rotting rewards, we introduce an algorithm that utilizes UCB with an adaptive sliding window, designed to manage the bias and variance trade-off arising due to rotting rewards. Our proposed algorithm achieves tight regret bounds for both slow and abrupt rotting scenarios. Lastly, we demonstrate the performance of our algorithms using synthetic datasets.

On the convergence of loss and uncertainty-based active learning algorithms

We study convergence rates of loss and uncertainty-based active learning algorithms under various assumptions. First, we provide a set of conditions under which a convergence rate guarantee holds, and use this for linear classifiers and linearly separable datasets to show convergence rate guarantees for loss-based sampling and different loss functions. Second, we provide a framework that allows us to derive convergence rate bounds for loss-based sampling by deploying known convergence rate bounds for stochastic gradient descent algorithms. Third, and last, we propose an active learning algorithm that combines sampling of points and stochastic Polyak's step size. We show a condition on the sampling that ensures a convergence rate guarantee for this algorithm for smooth convex loss functions. Our numerical results demonstrate efficiency of our proposed algorithm.

Rotting infinitely many-armed bandits

We consider the infinitely many-armed bandit problem with rotting rewards, where the mean reward of an arm decreases at each pull of the arm according to an arbitrary trend with maximum rotting rate $\varrho=o(1)$. We show that this learning problem has an $\Omega(\max\{\varrho^{1/3}T,\sqrt{T}\})$ worst-case regret lower bound where $T$ is the horizon time. We show that a matching upper bound $\tilde{O}(\max\{\varrho^{1/3}T,\sqrt{T}\})$, up to a poly-logarithmic factor, can be achieved by an algorithm that uses a UCB index for each arm and a threshold value to decide whether to continue pulling an arm or remove the arm from further consideration, when the algorithm knows the value of the maximum rotting rate $\varrho$. We also show that an $\tilde{O}(\max\{\varrho^{1/3}T,T^{3/4}\})$ regret upper bound can be achieved by an algorithm that does not know the value of $\varrho$, by using an adaptive UCB index along with an adaptive threshold value.

Scheduling Servers with Stochastic Bilinear Rewards

In this paper we study a multi-class, multi-server queueing system with stochastic rewards of job-server assignments following a bilinear model in feature vectors representing jobs and servers. Our goal is regret minimization against an oracle policy that has a complete information about system parameters. We propose a scheduling algorithm that uses a linear bandit algorithm along with dynamic allocation of jobs to servers. For the baseline setting, in which mean job service times are identical for all jobs, we show that our algorithm has a sub-linear regret, as well as a sub-linear bound on the mean queue length, in the horizon time. We further show that similar bounds hold under more general assumptions, allowing for non-identical mean job service times for different job classes and a time-varying set of server classes. We also show that better regret and mean queue length bounds can be guaranteed by an algorithm having access to traffic intensities of job classes. We present results of numerical experiments demonstrating how regret and mean queue length of our algorithms depend on various system parameters and compare their performance against a previously proposed algorithm using synthetic randomly generated data and a real-world cluster computing data trace.

Pure Exploration and Regret Minimization in Matching Bandits

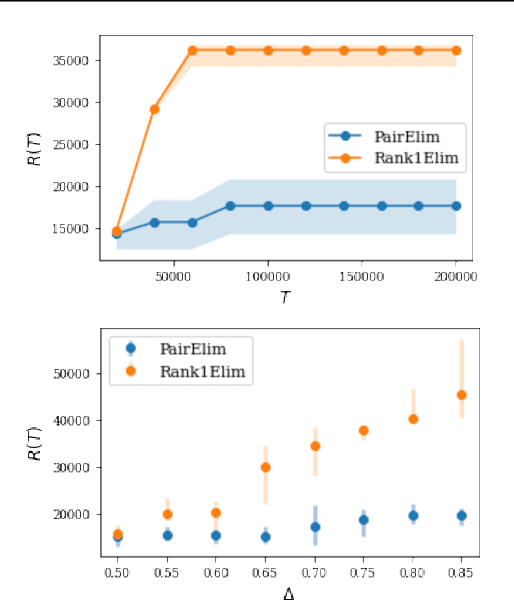
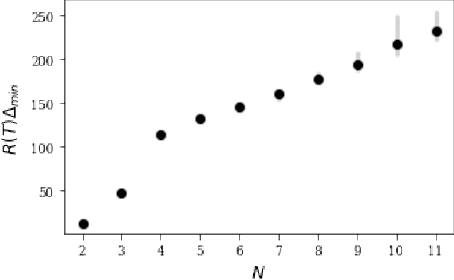
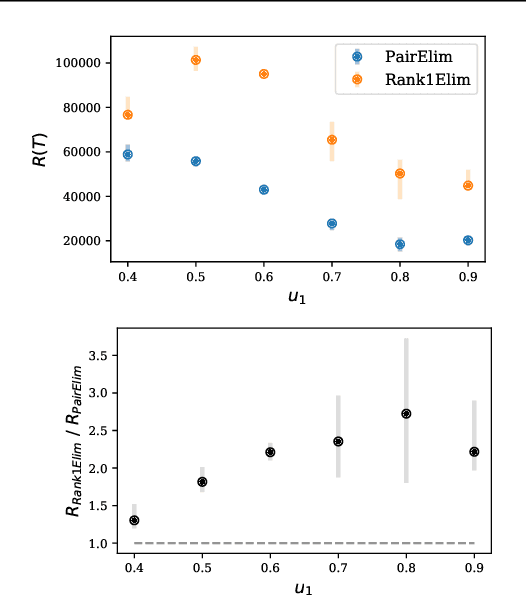
Finding an optimal matching in a weighted graph is a standard combinatorial problem. We consider its semi-bandit version where either a pair or a full matching is sampled sequentially. We prove that it is possible to leverage a rank-1 assumption on the adjacency matrix to reduce the sample complexity and the regret of off-the-shelf algorithms up to reaching a linear dependency in the number of vertices (up to poly log terms).

Learning to Schedule

This paper proposes a learning and scheduling algorithm to minimize the expected cumulative holding cost incurred by jobs, where statistical parameters defining their individual holding costs are unknown a priori. In each time slot, the server can process a job while receiving the realized random holding costs of the jobs remaining in the system. Our algorithm is a learning-based variant of the $c\mu$ rule for scheduling: it starts with a preemption period of fixed length which serves as a learning phase, and after accumulating enough data about individual jobs, it switches to nonpreemptive scheduling mode. The algorithm is designed to handle instances with large or small gaps in jobs' parameters and achieves near-optimal performance guarantees. The performance of our algorithm is captured by its regret, where the benchmark is the minimum possible cost attained when the statistical parameters of jobs are fully known. We prove upper bounds on the regret of our algorithm, and we derive a regret lower bound that is almost matching the proposed upper bounds. Our numerical results demonstrate the effectiveness of our algorithm and show that our theoretical regret analysis is nearly tight.

Test Score Algorithms for Budgeted Stochastic Utility Maximization

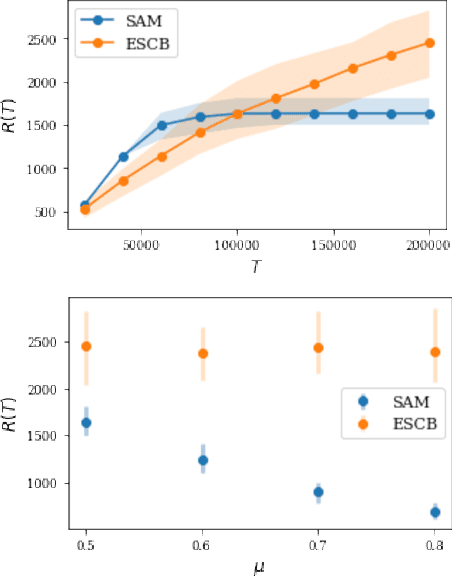
Motivated by recent developments in designing algorithms based on individual item scores for solving utility maximization problems, we study the framework of using test scores, defined as a statistic of observed individual item performance data, for solving the budgeted stochastic utility maximization problem. We extend an existing scoring mechanism, namely the replication test scores, to incorporate heterogeneous item costs as well as item values. We show that a natural greedy algorithm that selects items solely based on their replication test scores outputs solutions within a constant factor of the optimum for a broad class of utility functions. Our algorithms and approximation guarantees assume that test scores are noisy estimates of certain expected values with respect to marginal distributions of individual item values, thus making our algorithms practical and extending previous work that assumes noiseless estimates. Moreover, we show how our algorithm can be adapted to the setting where items arrive in a streaming fashion while maintaining the same approximation guarantee. We present numerical results, using synthetic data and data sets from the Academia.StackExchange Q&A forum, which show that our test score algorithm can achieve competitiveness, and in some cases better performance than a benchmark algorithm that requires access to a value oracle to evaluate function values.

Convergence Rates of Gradient Descent and MM Algorithms for Generalized Bradley-Terry Models

We show tight convergence rate bounds for gradient descent and MM algorithms for maximum likelihood estimation and maximum aposteriori probability estimation of a popular Bayesian inference method for generalized Bradley-Terry models. This class of models includes the Bradley-Terry model of paired comparisons, the Rao-Kupper model of paired comparisons with ties, the Luce choice model, and the Plackett-Luce ranking model. Our results show that MM algorithms have same convergence rates as gradient descent algorithms up to constant factors. For the maximum likelihood estimation, the convergence is linear with the rate crucially determined by the algebraic connectivity of the matrix of item pair co-occurrences in observed comparison data. For the Bayesian inference, the convergence rate is also linear, with the rate determined by a parameter of the prior distribution in a way that can make convergence arbitrarily slow for small values of this parameter. We propose a simple, first-order acceleration method that resolves the slow convergence issue.

Adaptive Matching for Expert Systems with Uncertain Task Types

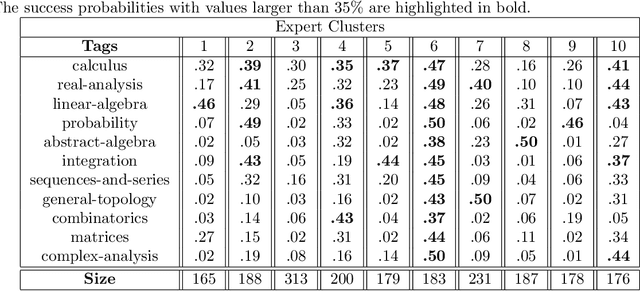
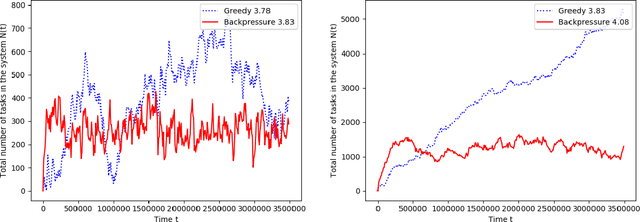
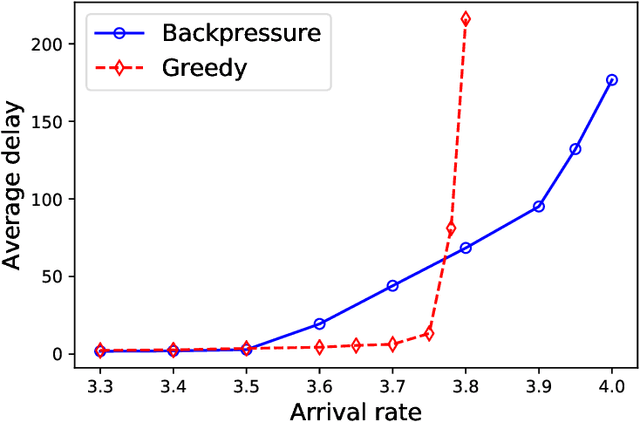
A matching in a two-sided market often incurs an externality: a matched resource may become unavailable to the other side of the market, at least for a while. This is especially an issue in online platforms involving human experts as the expert resources are often scarce. The efficient utilization of experts in these platforms is made challenging by the fact that the information available about the parties involved is usually limited. To address this challenge, we develop a model of a task-expert matching system where a task is matched to an expert using not only the prior information about the task but also the feedback obtained from the past matches. In our model the tasks arrive online while the experts are fixed and constrained by a finite service capacity. For this model, we characterize the maximum task resolution throughput a platform can achieve. We show that the natural greedy approaches where each expert is assigned a task most suitable to her skill is suboptimal, as it does not internalize the above externality. We develop a throughput optimal backpressure algorithm which does so by accounting for the `congestion' among different task types. Finally, we validate our model and confirm our theoretical findings with data-driven simulations via logs of Math.StackExchange, a StackOverflow forum dedicated to mathematics.

KONG: Kernels for ordered-neighborhood graphs

We present novel graph kernels for graphs with node and edge labels that have ordered neighborhoods, i.e. when neighbor nodes follow an order. Graphs with ordered neighborhoods are a natural data representation for evolving graphs where edges are created over time, which induces an order. Combining convolutional subgraph kernels and string kernels, we design new scalable algorithms for generation of explicit graph feature maps using sketching techniques. We obtain precise bounds for the approximation accuracy and computational complexity of the proposed approaches and demonstrate their applicability on real datasets. In particular, our experiments demonstrate that neighborhood ordering results in more informative features. For the special case of general graphs, i.e. graphs without ordered neighborhoods, the new graph kernels yield efficient and simple algorithms for the comparison of label distributions between graphs.