Regret-Minimization Algorithms for Multi-Agent Cooperative Learning Systems

A Multi-Agent Cooperative Learning (MACL) system is an artificial intelligence (AI) system where multiple learning agents work together to complete a common task. Recent empirical success of MACL systems in various domains (e.g. traffic control, cloud computing, robotics) has sparked active research into the design and analysis of MACL systems for sequential decision making problems. One important metric of the learning algorithm for decision making problems is its regret, i.e. the difference between the highest achievable reward and the actual reward that the algorithm gains. The design and development of a MACL system with low-regret learning algorithms can create huge economic values. In this thesis, I analyze MACL systems for different sequential decision making problems. Concretely, the Chapter 3 and 4 investigate the cooperative multi-agent multi-armed bandit problems, with full-information or bandit feedback, in which multiple learning agents can exchange their information through a communication network and the agents can only observe the rewards of the actions they choose. Chapter 5 considers the communication-regret trade-off for online convex optimization in the distributed setting. Chapter 6 discusses how to form high-productive teams for agents based on their unknown but fixed types using adaptive incremental matchings. For the above problems, I present the regret lower bounds for feasible learning algorithms and provide the efficient algorithms to achieve this bound. The regret bounds I present in Chapter 3, 4 and 5 quantify how the regret depends on the connectivity of the communication network and the communication delay, thus giving useful guidance on design of the communication protocol in MACL systems

Doubly Adversarial Federated Bandits

We study a new non-stochastic federated multi-armed bandit problem with multiple agents collaborating via a communication network. The losses of the arms are assigned by an oblivious adversary that specifies the loss of each arm not only for each time step but also for each agent, which we call ``doubly adversarial". In this setting, different agents may choose the same arm in the same time step but observe different feedback. The goal of each agent is to find a globally best arm in hindsight that has the lowest cumulative loss averaged over all agents, which necessities the communication among agents. We provide regret lower bounds for any federated bandit algorithm under different settings, when agents have access to full-information feedback, or the bandit feedback. For the bandit feedback setting, we propose a near-optimal federated bandit algorithm called FEDEXP3. Our algorithm gives a positive answer to an open question proposed in Cesa-Bianchi et al. (2016): FEDEXP3 can guarantee a sub-linear regret without exchanging sequences of selected arm identities or loss sequences among agents. We also provide numerical evaluations of our algorithm to validate our theoretical results and demonstrate its effectiveness on synthetic and real-world datasets

On Regret-optimal Cooperative Nonstochastic Multi-armed Bandits

We consider the nonstochastic multi-agent multi-armed bandit problem with agents collaborating via a communication network with delays. We show a lower bound for individual regret of all agents. We show that with suitable regularizers and communication protocols, a collaborative multi-agent \emph{follow-the-regularized-leader} (FTRL) algorithm has an individual regret upper bound that matches the lower bound up to a constant factor when the number of arms is large enough relative to degrees of agents in the communication graph. We also show that an FTRL algorithm with a suitable regularizer is regret optimal with respect to the scaling with the edge-delay parameter. We present numerical experiments validating our theoretical results and demonstrate cases when our algorithms outperform previously proposed algorithms.

Pure Exploration and Regret Minimization in Matching Bandits

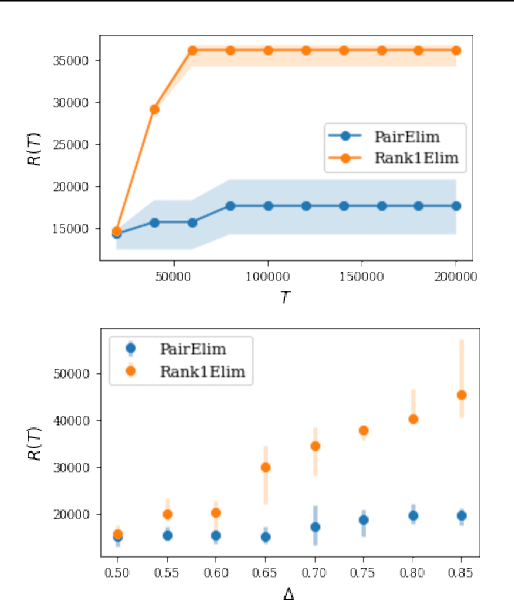
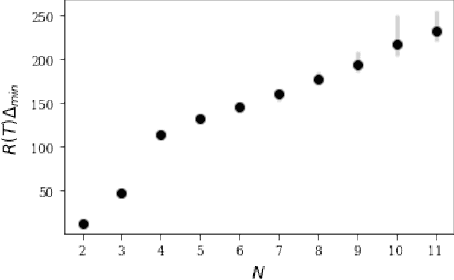
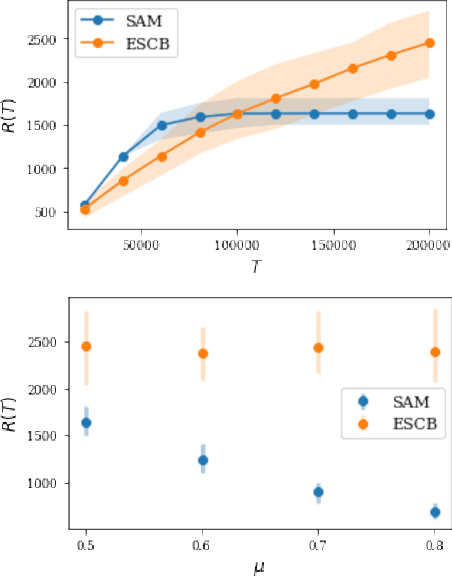
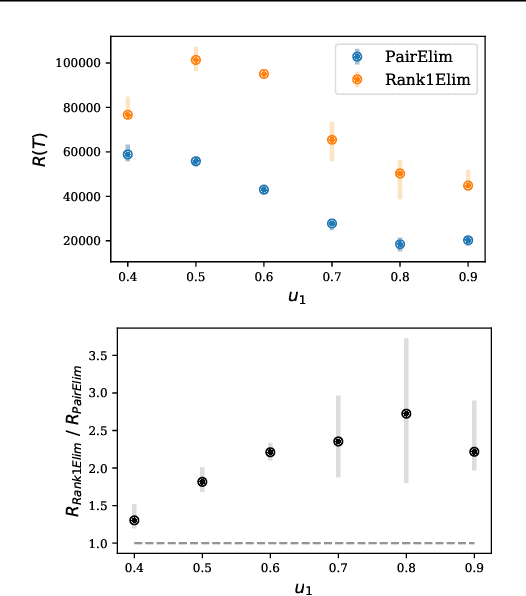
Finding an optimal matching in a weighted graph is a standard combinatorial problem. We consider its semi-bandit version where either a pair or a full matching is sampled sequentially. We prove that it is possible to leverage a rank-1 assumption on the adjacency matrix to reduce the sample complexity and the regret of off-the-shelf algorithms up to reaching a linear dependency in the number of vertices (up to poly log terms).