Strategic Arms with Side Communication Prevail Over Low-Regret MAB Algorithms

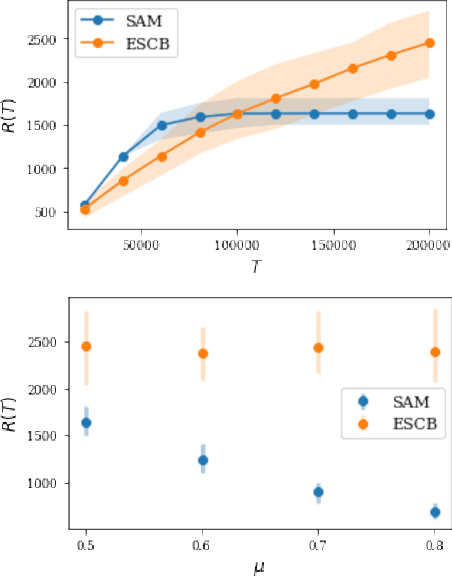
In the strategic multi-armed bandit setting, when arms possess perfect information about the player's behavior, they can establish an equilibrium where: 1. they retain almost all of their value, 2. they leave the player with a substantial (linear) regret. This study illustrates that, even if complete information is not publicly available to all arms but is shared among them, it is possible to achieve a similar equilibrium. The primary challenge lies in designing a communication protocol that incentivizes the arms to communicate truthfully.

Robust Consensus in Ranking Data Analysis: Definitions, Properties and Computational Issues

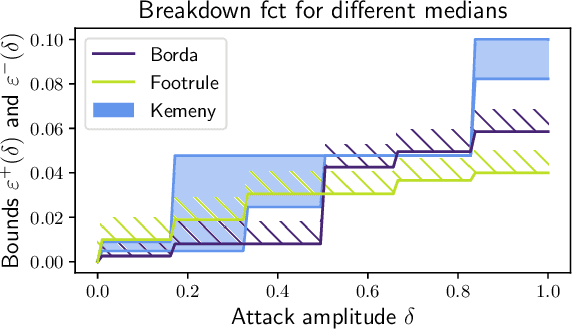
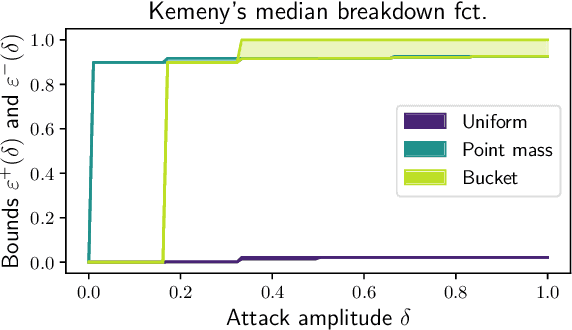
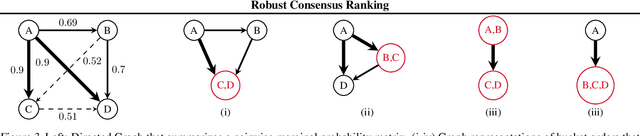
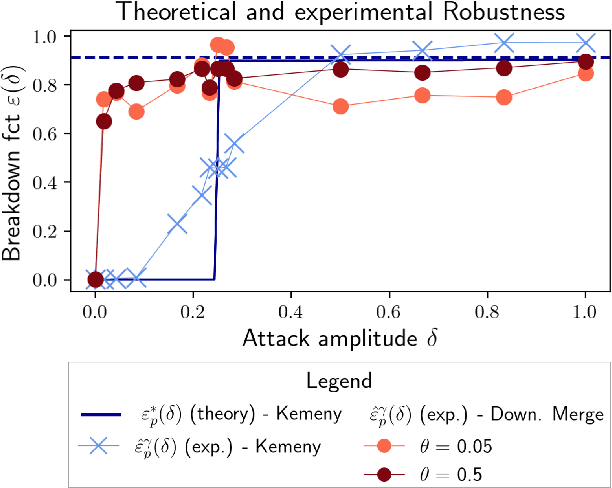
As the issue of robustness in AI systems becomes vital, statistical learning techniques that are reliable even in presence of partly contaminated data have to be developed. Preference data, in the form of (complete) rankings in the simplest situations, are no exception and the demand for appropriate concepts and tools is all the more pressing given that technologies fed by or producing this type of data (e.g. search engines, recommending systems) are now massively deployed. However, the lack of vector space structure for the set of rankings (i.e. the symmetric group $\mathfrak{S}_n$) and the complex nature of statistics considered in ranking data analysis make the formulation of robustness objectives in this domain challenging. In this paper, we introduce notions of robustness, together with dedicated statistical methods, for Consensus Ranking the flagship problem in ranking data analysis, aiming at summarizing a probability distribution on $\mathfrak{S}_n$ by a median ranking. Precisely, we propose specific extensions of the popular concept of breakdown point, tailored to consensus ranking, and address the related computational issues. Beyond the theoretical contributions, the relevance of the approach proposed is supported by an experimental study.

Jointly Efficient and Optimal Algorithms for Logistic Bandits

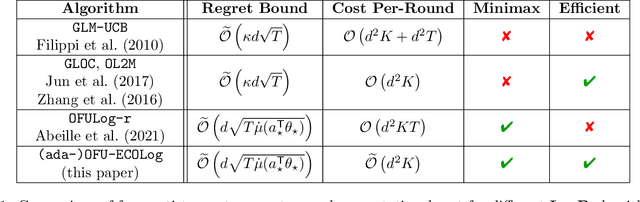
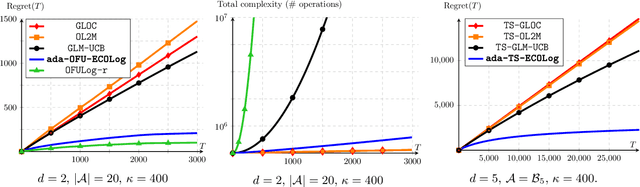
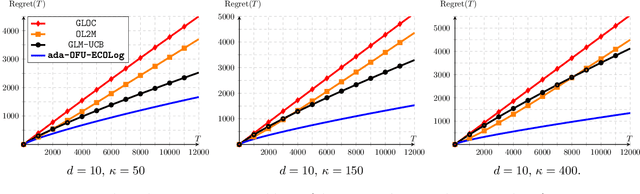
Logistic Bandits have recently undergone careful scrutiny by virtue of their combined theoretical and practical relevance. This research effort delivered statistically efficient algorithms, improving the regret of previous strategies by exponentially large factors. Such algorithms are however strikingly costly as they require $\Omega(t)$ operations at each round. On the other hand, a different line of research focused on computational efficiency ($\mathcal{O}(1)$ per-round cost), but at the cost of letting go of the aforementioned exponential improvements. Obtaining the best of both world is unfortunately not a matter of marrying both approaches. Instead we introduce a new learning procedure for Logistic Bandits. It yields confidence sets which sufficient statistics can be easily maintained online without sacrificing statistical tightness. Combined with efficient planning mechanisms we design fast algorithms which regret performance still match the problem-dependent lower-bound of Abeille et al. (2021). To the best of our knowledge, those are the first Logistic Bandit algorithms that simultaneously enjoy statistical and computational efficiency.

Pure Exploration and Regret Minimization in Matching Bandits

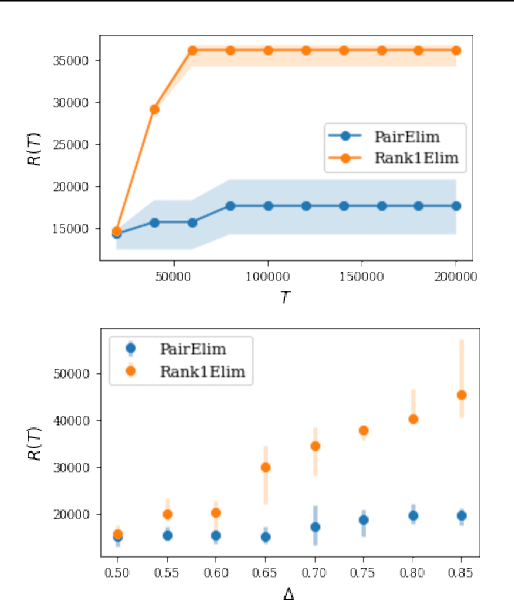
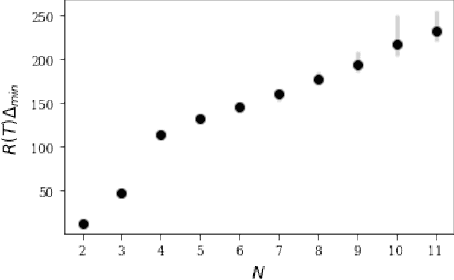
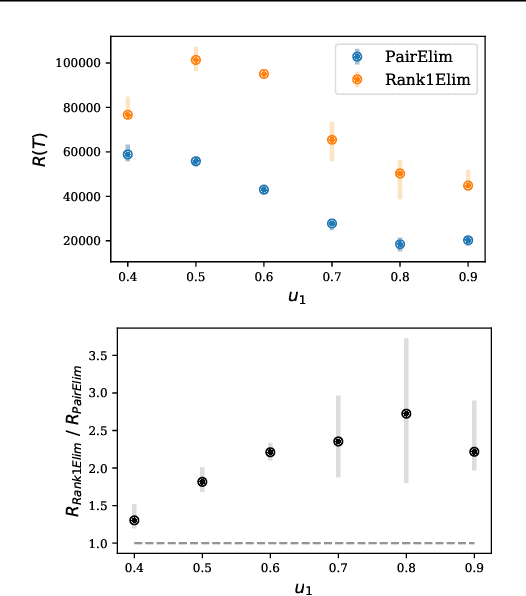
Finding an optimal matching in a weighted graph is a standard combinatorial problem. We consider its semi-bandit version where either a pair or a full matching is sampled sequentially. We prove that it is possible to leverage a rank-1 assumption on the adjacency matrix to reduce the sample complexity and the regret of off-the-shelf algorithms up to reaching a linear dependency in the number of vertices (up to poly log terms).

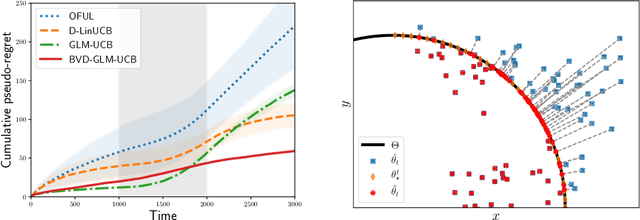
Regret Bounds for Generalized Linear Bandits under Parameter Drift

Generalized Linear Bandits (GLBs) are powerful extensions to the Linear Bandit (LB) setting, broadening the benefits of reward parametrization beyond linearity. In this paper we study GLBs in non-stationary environments, characterized by a general metric of non-stationarity known as the variation-budget or \emph{parameter-drift}, denoted $B_T$. While previous attempts have been made to extend LB algorithms to this setting, they overlook a salient feature of GLBs which flaws their results. In this work, we introduce a new algorithm that addresses this difficulty. We prove that under a geometric assumption on the action set, our approach enjoys a $\tilde{\mathcal{O}}(B_T^{1/3}T^{2/3})$ regret bound. In the general case, we show that it suffers at most a $\tilde{\mathcal{O}}(B_T^{1/5}T^{4/5})$ regret. At the core of our contribution is a generalization of the projection step introduced in Filippi et al. (2010), adapted to the non-stationary nature of the problem. Our analysis sheds light on central mechanisms inherited from the setting by explicitly splitting the treatment of the learning and tracking aspects of the problem.

Wasserstein Learning of Determinantal Point Processes

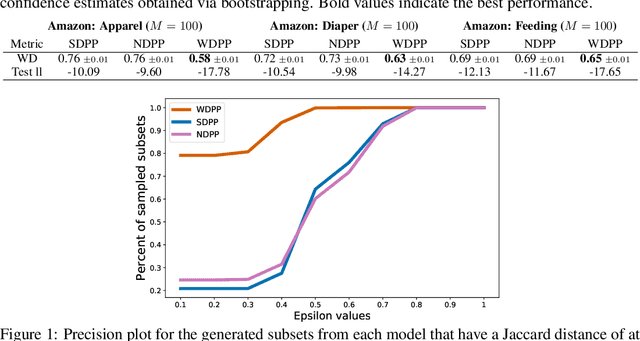
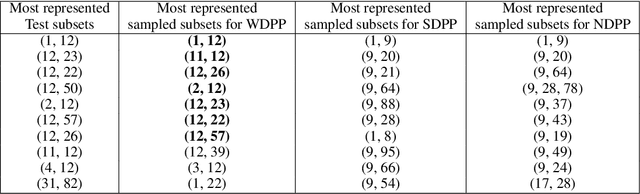
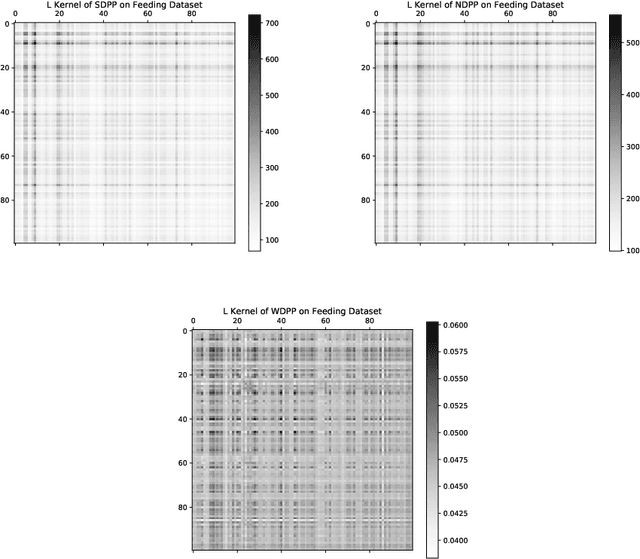
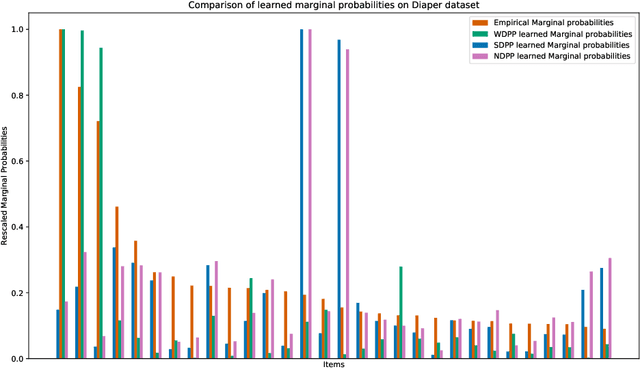
Determinantal point processes (DPPs) have received significant attention as an elegant probabilistic model for discrete subset selection. Most prior work on DPP learning focuses on maximum likelihood estimation (MLE). While efficient and scalable, MLE approaches do not leverage any subset similarity information and may fail to recover the true generative distribution of discrete data. In this work, by deriving a differentiable relaxation of a DPP sampling algorithm, we present a novel approach for learning DPPs that minimizes the Wasserstein distance between the model and data composed of observed subsets. Through an evaluation on a real-world dataset, we show that our Wasserstein learning approach provides significantly improved predictive performance on a generative task compared to DPPs trained using MLE.

Instance-Wise Minimax-Optimal Algorithms for Logistic Bandits

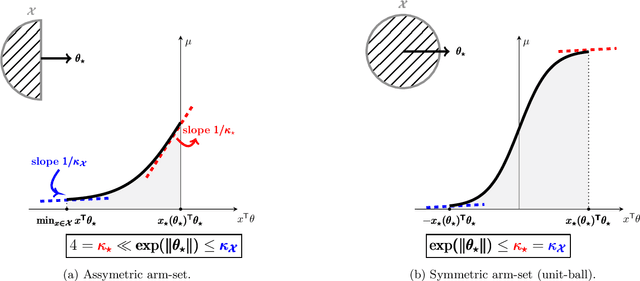
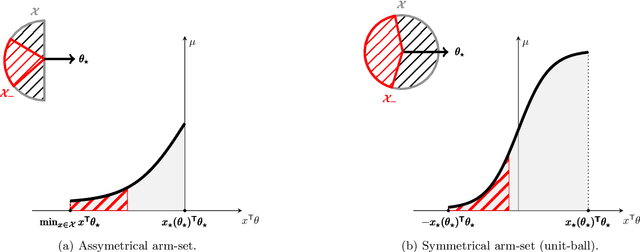
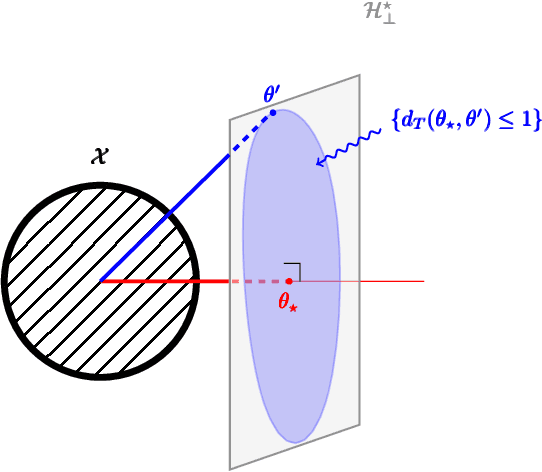
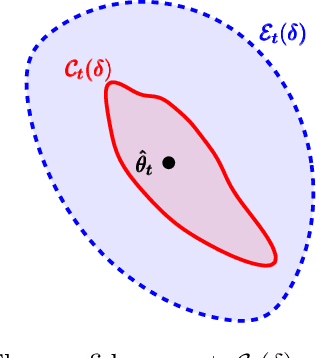
Logistic Bandits have recently attracted substantial attention, by providing an uncluttered yet challenging framework for understanding the impact of non-linearity in parametrized bandits. It was shown by Faury et al. (2020) that the learning-theoretic difficulties of Logistic Bandits can be embodied by a large (sometimes prohibitively) problem-dependent constant $\kappa$, characterizing the magnitude of the reward's non-linearity. In this paper we introduce a novel algorithm for which we provide a refined analysis. This allows for a better characterization of the effect of non-linearity and yields improved problem-dependent guarantees. In most favorable cases this leads to a regret upper-bound scaling as $\tilde{\mathcal{O}}(d\sqrt{T/\kappa})$, which dramatically improves over the $\tilde{\mathcal{O}}(d\sqrt{T}+\kappa)$ state-of-the-art guarantees. We prove that this rate is minimax-optimal by deriving a $\Omega(d\sqrt{T/\kappa})$ problem-dependent lower-bound. Our analysis identifies two regimes (permanent and transitory) of the regret, which ultimately re-conciliates Faury et al. (2020) with the Bayesian approach of Dong et al. (2019). In contrast to previous works, we find that in the permanent regime non-linearity can dramatically ease the exploration-exploitation trade-off. While it also impacts the length of the transitory phase in a problem-dependent fashion, we show that this impact is mild in most reasonable configurations.

Real-Time Optimisation for Online Learning in Auctions

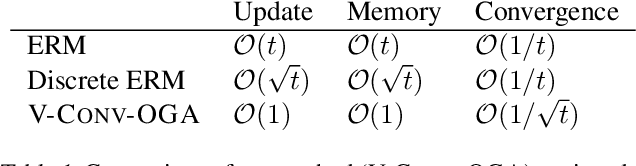
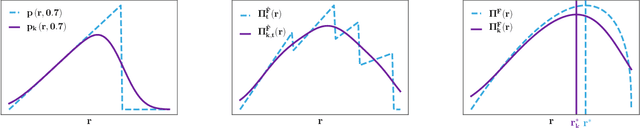
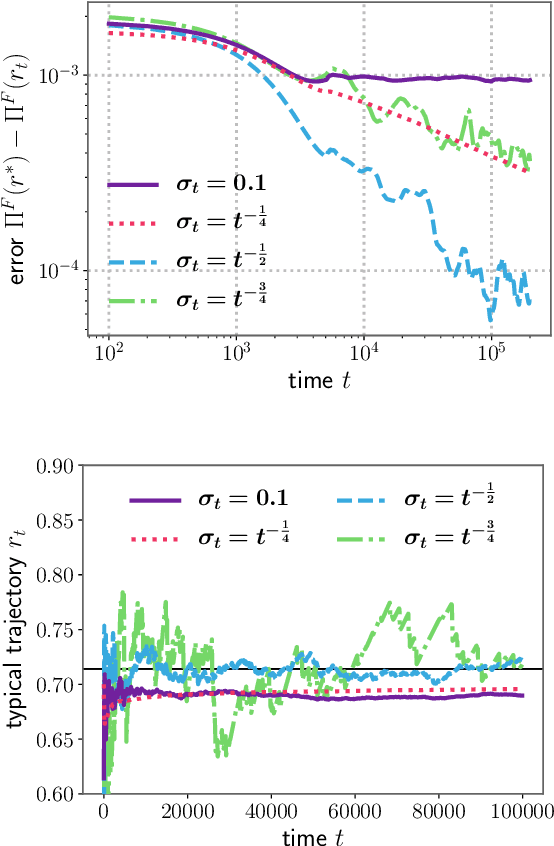
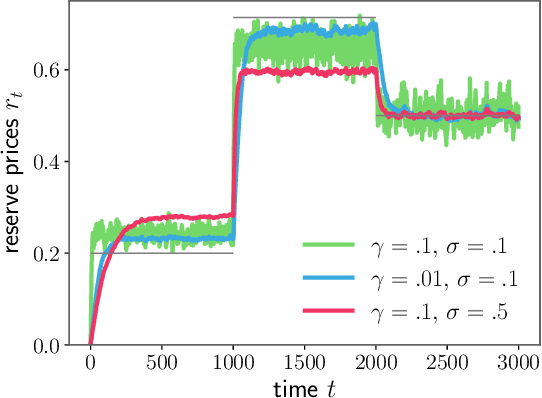
In display advertising, a small group of sellers and bidders face each other in up to 10 12 auctions a day. In this context, revenue maximisation via monopoly price learning is a high-value problem for sellers. By nature, these auctions are online and produce a very high frequency stream of data. This results in a computational strain that requires algorithms be real-time. Unfortunately, existing methods inherited from the batch setting suffer O($\sqrt t$) time/memory complexity at each update, prohibiting their use. In this paper, we provide the first algorithm for online learning of monopoly prices in online auctions whose update is constant in time and memory.

Do Not Mask What You Do Not Need to Mask: a Parser-Free Virtual Try-On

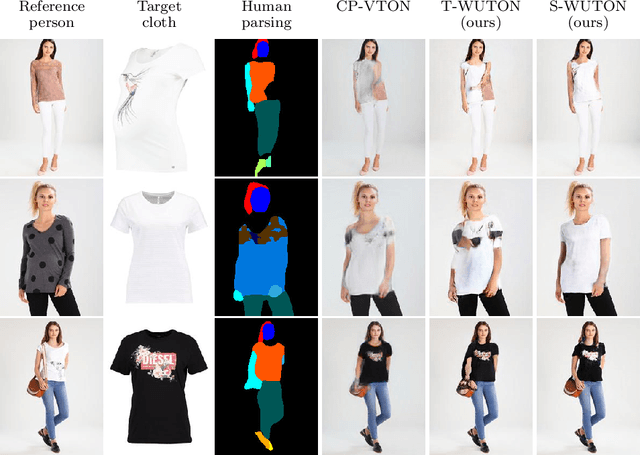
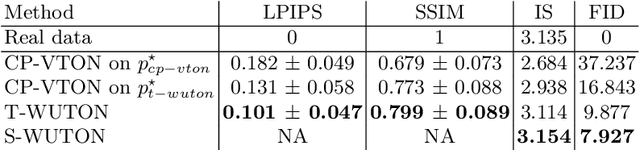
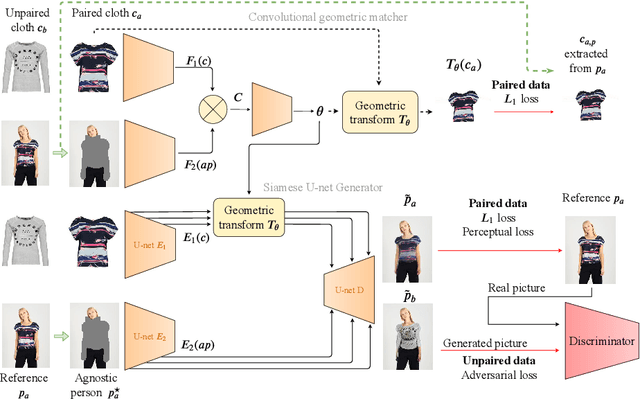
The 2D virtual try-on task has recently attracted a great interest from the research community, for its direct potential applications in online shopping as well as for its inherent and non-addressed scientific challenges. This task requires fitting an in-shop cloth image on the image of a person, which is highly challenging because it involves cloth warping, image compositing, and synthesizing. Casting virtual try-on into a supervised task faces a difficulty: available datasets are composed of pairs of pictures (cloth, person wearing the cloth). Thus, we have no access to ground-truth when the cloth on the person changes. State-of-the-art models solve this by masking the cloth information on the person with both a human parser and a pose estimator. Then, image synthesis modules are trained to reconstruct the person image from the masked person image and the cloth image. This procedure has several caveats: firstly, human parsers are prone to errors; secondly, it is a costly pre-processing step, which also has to be applied at inference time; finally, it makes the task harder than it is since the mask covers information that should be kept such as hands or accessories. In this paper, we propose a novel student-teacher paradigm where the teacher is trained in the standard way (reconstruction) before guiding the student to focus on the initial task (changing the cloth). The student additionally learns from an adversarial loss, which pushes it to follow the distribution of the real images. Consequently, the student exploits information that is masked to the teacher. A student trained without the adversarial loss would not use this information. Also, getting rid of both human parser and pose estimator at inference time allows obtaining a real-time virtual try-on.

Improved Optimistic Algorithms for Logistic Bandits

The generalized linear bandit framework has attracted a lot of attention in recent years by extending the well-understood linear setting and allowing to model richer reward structures. It notably covers the logistic model, widely used when rewards are binary. For logistic bandits, the frequentist regret guarantees of existing algorithms are $\tilde{\mathcal{O}}(\kappa \sqrt{T})$, where $\kappa$ is a problem-dependent constant. Unfortunately, $\kappa$ can be arbitrarily large as it scales exponentially with the size of the decision set. This may lead to significantly loose regret bounds and poor empirical performance. In this work, we study the logistic bandit with a focus on the prohibitive dependencies introduced by $\kappa$. We propose a new optimistic algorithm based on a finer examination of the non-linearities of the reward function. We show that it enjoys a $\tilde{\mathcal{O}}(\sqrt{T})$ regret with no dependency in $\kappa$, but for a second order term. Our analysis is based on a new tail-inequality for self-normalized martingales, of independent interest.