Bandit Optimal Transport

Despite the impressive progress in statistical Optimal Transport (OT) in recent years, there has been little interest in the study of the \emph{sequential learning} of OT. Surprisingly so, as this problem is both practically motivated and a challenging extension of existing settings such as linear bandits. This article considers (for the first time) the stochastic bandit problem of learning to solve generic Kantorovich and entropic OT problems from repeated interactions when the marginals are known but the cost is unknown. We provide $\tilde{\mathcal O}(\sqrt{T})$ regret algorithms for both problems by extending linear bandits on Hilbert spaces. These results provide a reduction to infinite-dimensional linear bandits. To deal with the dimension, we provide a method to exploit the intrinsic regularity of the cost to learn, yielding corresponding regret bounds which interpolate between $\tilde{\mathcal O}(\sqrt{T})$ and $\tilde{\mathcal O}(T)$.

Pareto-Optimality, Smoothness, and Stochasticity in Learning-Augmented One-Max-Search

One-max search is a classic problem in online decision-making, in which a trader acts on a sequence of revealed prices and accepts one of them irrevocably to maximise its profit. The problem has been studied both in probabilistic and in worst-case settings, notably through competitive analysis, and more recently in learning-augmented settings in which the trader has access to a prediction on the sequence. However, existing approaches either lack smoothness, or do not achieve optimal worst-case guarantees: they do not attain the best possible trade-off between the consistency and the robustness of the algorithm. We close this gap by presenting the first algorithm that simultaneously achieves both of these important objectives. Furthermore, we show how to leverage the obtained smoothness to provide an analysis of one-max search in stochastic learning-augmented settings which capture randomness in both the observed prices and the prediction.

Near-continuous time Reinforcement Learning for continuous state-action spaces

We consider the Reinforcement Learning problem of controlling an unknown dynamical system to maximise the long-term average reward along a single trajectory. Most of the literature considers system interactions that occur in discrete time and discrete state-action spaces. Although this standpoint is suitable for games, it is often inadequate for mechanical or digital systems in which interactions occur at a high frequency, if not in continuous time, and whose state spaces are large if not inherently continuous. Perhaps the only exception is the Linear Quadratic framework for which results exist both in discrete and continuous time. However, its ability to handle continuous states comes with the drawback of a rigid dynamic and reward structure. This work aims to overcome these shortcomings by modelling interaction times with a Poisson clock of frequency $\varepsilon^{-1}$, which captures arbitrary time scales: from discrete ($\varepsilon=1$) to continuous time ($\varepsilon\downarrow0$). In addition, we consider a generic reward function and model the state dynamics according to a jump process with an arbitrary transition kernel on $\mathbb{R}^d$. We show that the celebrated optimism protocol applies when the sub-tasks (learning and planning) can be performed effectively. We tackle learning within the eluder dimension framework and propose an approximate planning method based on a diffusive limit approximation of the jump process. Overall, our algorithm enjoys a regret of order $\tilde{\mathcal{O}}(\varepsilon^{1/2} T+\sqrt{T})$. As the frequency of interactions blows up, the approximation error $\varepsilon^{1/2} T$ vanishes, showing that $\tilde{\mathcal{O}}(\sqrt{T})$ is attainable in near-continuous time.

Real-Time Optimisation for Online Learning in Auctions

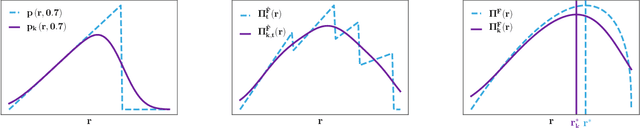
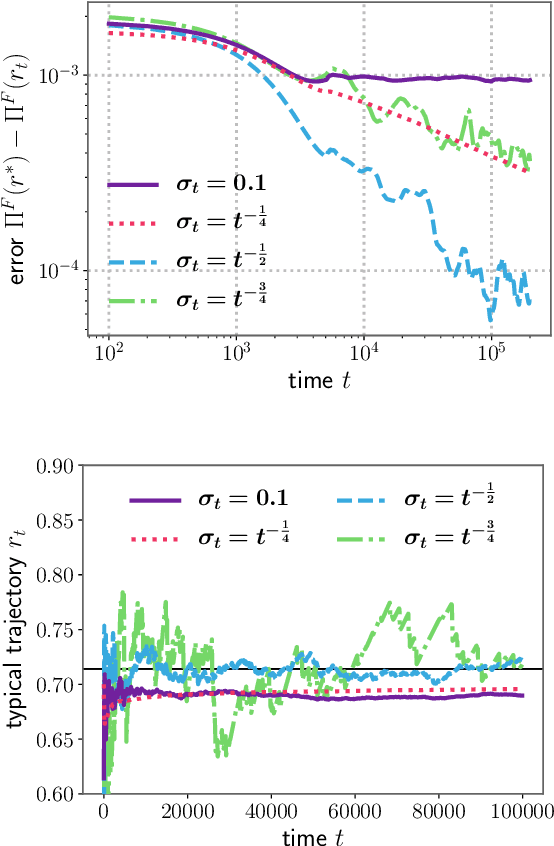
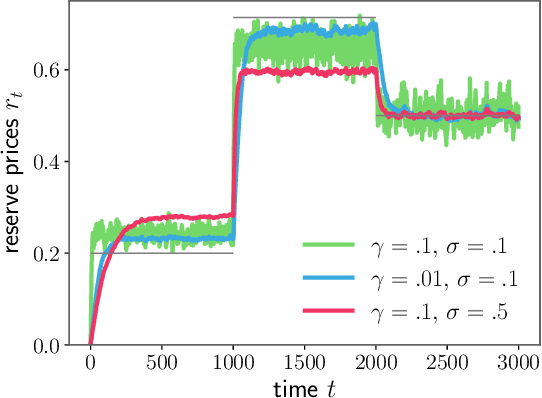
In display advertising, a small group of sellers and bidders face each other in up to 10 12 auctions a day. In this context, revenue maximisation via monopoly price learning is a high-value problem for sellers. By nature, these auctions are online and produce a very high frequency stream of data. This results in a computational strain that requires algorithms be real-time. Unfortunately, existing methods inherited from the batch setting suffer O($\sqrt t$) time/memory complexity at each update, prohibiting their use. In this paper, we provide the first algorithm for online learning of monopoly prices in online auctions whose update is constant in time and memory.