Marc Abeille
CEREMADE
Multi-Armed Bandits with Minimum Aggregated Revenue Constraints
Oct 14, 2025Abstract:We examine a multi-armed bandit problem with contextual information, where the objective is to ensure that each arm receives a minimum aggregated reward across contexts while simultaneously maximizing the total cumulative reward. This framework captures a broad class of real-world applications where fair revenue allocation is critical and contextual variation is inherent. The cross-context aggregation of minimum reward constraints, while enabling better performance and easier feasibility, introduces significant technical challenges -- particularly the absence of closed-form optimal allocations typically available in standard MAB settings. We design and analyze algorithms that either optimistically prioritize performance or pessimistically enforce constraint satisfaction. For each algorithm, we derive problem-dependent upper bounds on both regret and constraint violations. Furthermore, we establish a lower bound demonstrating that the dependence on the time horizon in our results is optimal in general and revealing fundamental limitations of the free exploration principle leveraged in prior work.
When and why randomised exploration works (in linear bandits)
Feb 13, 2025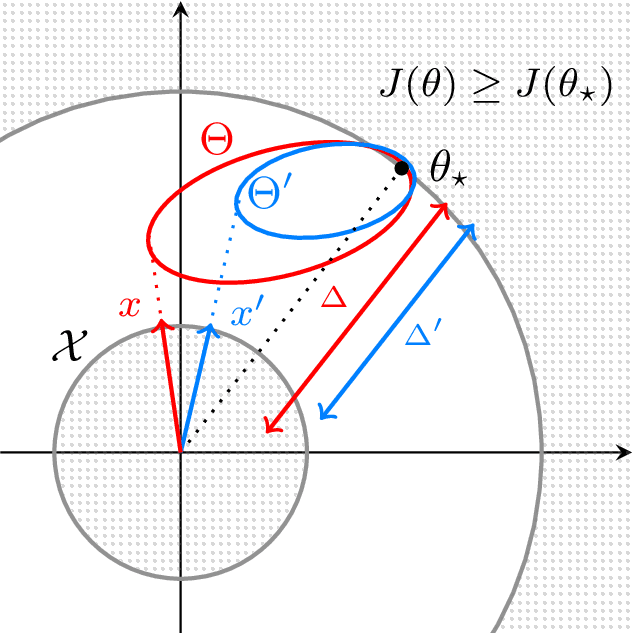
Abstract:We provide an approach for the analysis of randomised exploration algorithms like Thompson sampling that does not rely on forced optimism or posterior inflation. With this, we demonstrate that in the $d$-dimensional linear bandit setting, when the action space is smooth and strongly convex, randomised exploration algorithms enjoy an $n$-step regret bound of the order $O(d\sqrt{n} \log(n))$. Notably, this shows for the first time that there exist non-trivial linear bandit settings where Thompson sampling can achieve optimal dimension dependence in the regret.
Near-continuous time Reinforcement Learning for continuous state-action spaces
Sep 06, 2023Abstract:We consider the Reinforcement Learning problem of controlling an unknown dynamical system to maximise the long-term average reward along a single trajectory. Most of the literature considers system interactions that occur in discrete time and discrete state-action spaces. Although this standpoint is suitable for games, it is often inadequate for mechanical or digital systems in which interactions occur at a high frequency, if not in continuous time, and whose state spaces are large if not inherently continuous. Perhaps the only exception is the Linear Quadratic framework for which results exist both in discrete and continuous time. However, its ability to handle continuous states comes with the drawback of a rigid dynamic and reward structure. This work aims to overcome these shortcomings by modelling interaction times with a Poisson clock of frequency $\varepsilon^{-1}$, which captures arbitrary time scales: from discrete ($\varepsilon=1$) to continuous time ($\varepsilon\downarrow0$). In addition, we consider a generic reward function and model the state dynamics according to a jump process with an arbitrary transition kernel on $\mathbb{R}^d$. We show that the celebrated optimism protocol applies when the sub-tasks (learning and planning) can be performed effectively. We tackle learning within the eluder dimension framework and propose an approximate planning method based on a diffusive limit approximation of the jump process. Overall, our algorithm enjoys a regret of order $\tilde{\mathcal{O}}(\varepsilon^{1/2} T+\sqrt{T})$. As the frequency of interactions blows up, the approximation error $\varepsilon^{1/2} T$ vanishes, showing that $\tilde{\mathcal{O}}(\sqrt{T})$ is attainable in near-continuous time.
Jointly Efficient and Optimal Algorithms for Logistic Bandits
Jan 19, 2022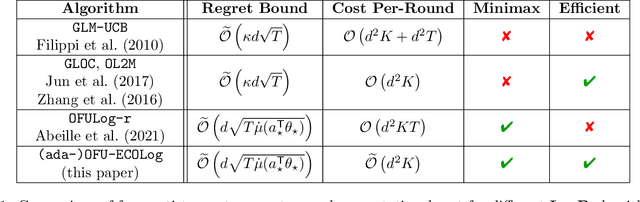
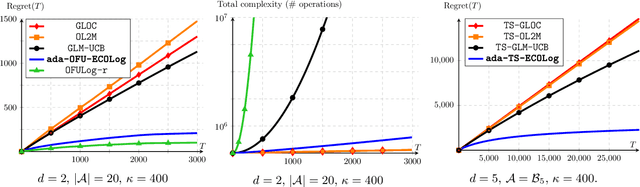
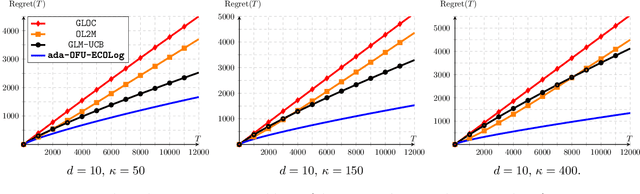
Abstract:Logistic Bandits have recently undergone careful scrutiny by virtue of their combined theoretical and practical relevance. This research effort delivered statistically efficient algorithms, improving the regret of previous strategies by exponentially large factors. Such algorithms are however strikingly costly as they require $\Omega(t)$ operations at each round. On the other hand, a different line of research focused on computational efficiency ($\mathcal{O}(1)$ per-round cost), but at the cost of letting go of the aforementioned exponential improvements. Obtaining the best of both world is unfortunately not a matter of marrying both approaches. Instead we introduce a new learning procedure for Logistic Bandits. It yields confidence sets which sufficient statistics can be easily maintained online without sacrificing statistical tightness. Combined with efficient planning mechanisms we design fast algorithms which regret performance still match the problem-dependent lower-bound of Abeille et al. (2021). To the best of our knowledge, those are the first Logistic Bandit algorithms that simultaneously enjoy statistical and computational efficiency.
Regret Bounds for Generalized Linear Bandits under Parameter Drift
Mar 09, 2021
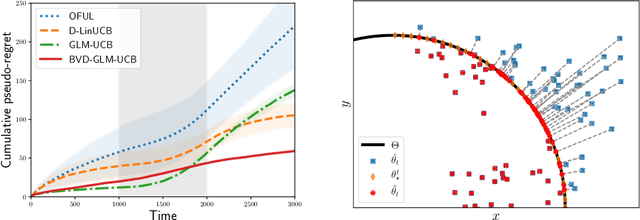
Abstract:Generalized Linear Bandits (GLBs) are powerful extensions to the Linear Bandit (LB) setting, broadening the benefits of reward parametrization beyond linearity. In this paper we study GLBs in non-stationary environments, characterized by a general metric of non-stationarity known as the variation-budget or \emph{parameter-drift}, denoted $B_T$. While previous attempts have been made to extend LB algorithms to this setting, they overlook a salient feature of GLBs which flaws their results. In this work, we introduce a new algorithm that addresses this difficulty. We prove that under a geometric assumption on the action set, our approach enjoys a $\tilde{\mathcal{O}}(B_T^{1/3}T^{2/3})$ regret bound. In the general case, we show that it suffers at most a $\tilde{\mathcal{O}}(B_T^{1/5}T^{4/5})$ regret. At the core of our contribution is a generalization of the projection step introduced in Filippi et al. (2010), adapted to the non-stationary nature of the problem. Our analysis sheds light on central mechanisms inherited from the setting by explicitly splitting the treatment of the learning and tracking aspects of the problem.
Instance-Wise Minimax-Optimal Algorithms for Logistic Bandits
Oct 23, 2020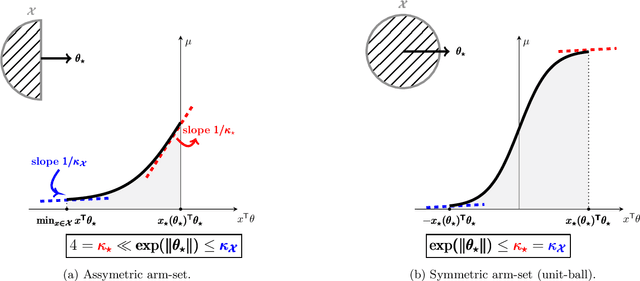
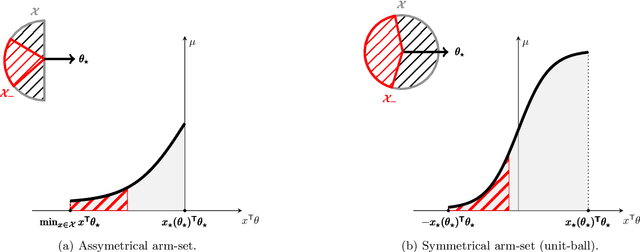
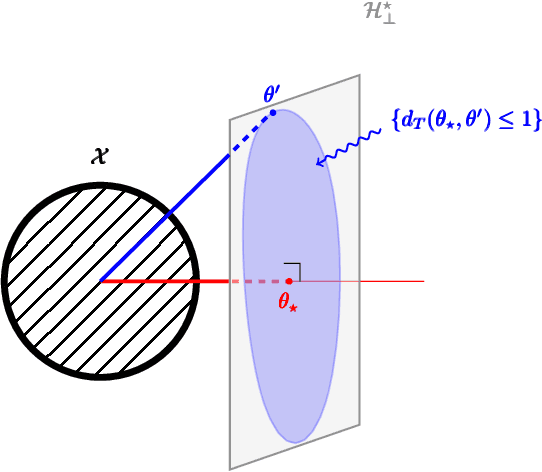
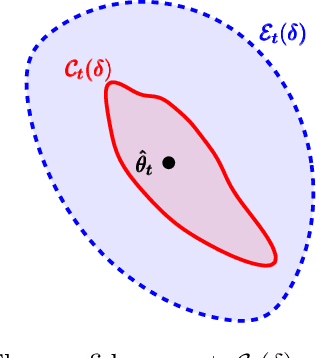
Abstract:Logistic Bandits have recently attracted substantial attention, by providing an uncluttered yet challenging framework for understanding the impact of non-linearity in parametrized bandits. It was shown by Faury et al. (2020) that the learning-theoretic difficulties of Logistic Bandits can be embodied by a large (sometimes prohibitively) problem-dependent constant $\kappa$, characterizing the magnitude of the reward's non-linearity. In this paper we introduce a novel algorithm for which we provide a refined analysis. This allows for a better characterization of the effect of non-linearity and yields improved problem-dependent guarantees. In most favorable cases this leads to a regret upper-bound scaling as $\tilde{\mathcal{O}}(d\sqrt{T/\kappa})$, which dramatically improves over the $\tilde{\mathcal{O}}(d\sqrt{T}+\kappa)$ state-of-the-art guarantees. We prove that this rate is minimax-optimal by deriving a $\Omega(d\sqrt{T/\kappa})$ problem-dependent lower-bound. Our analysis identifies two regimes (permanent and transitory) of the regret, which ultimately re-conciliates Faury et al. (2020) with the Bayesian approach of Dong et al. (2019). In contrast to previous works, we find that in the permanent regime non-linearity can dramatically ease the exploration-exploitation trade-off. While it also impacts the length of the transitory phase in a problem-dependent fashion, we show that this impact is mild in most reasonable configurations.
Real-Time Optimisation for Online Learning in Auctions
Oct 20, 2020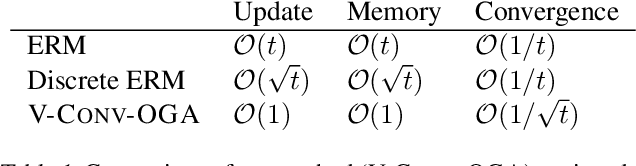
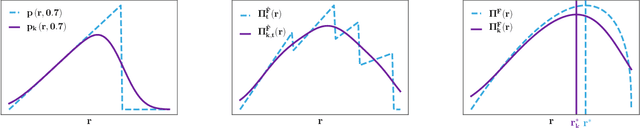
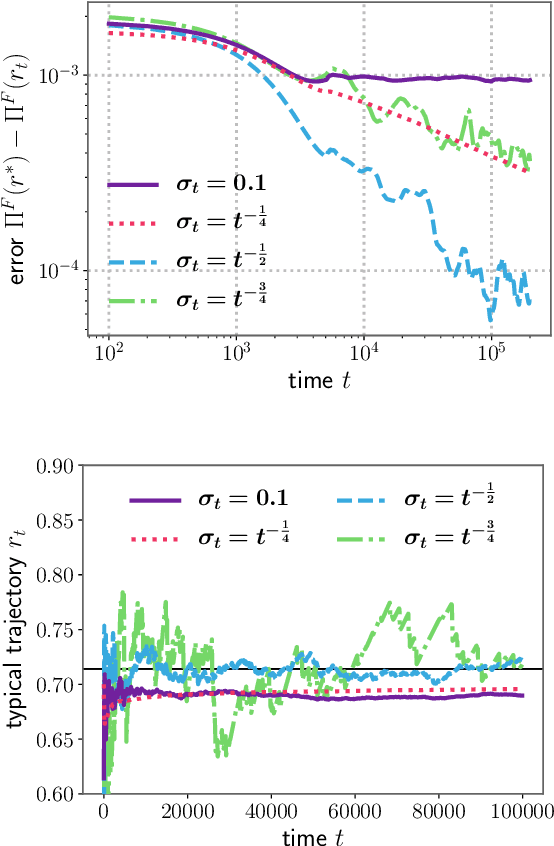
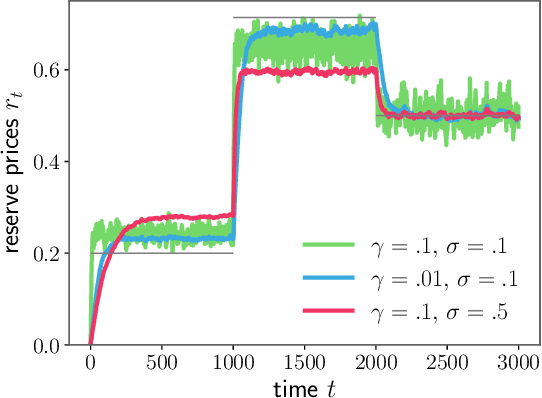
Abstract:In display advertising, a small group of sellers and bidders face each other in up to 10 12 auctions a day. In this context, revenue maximisation via monopoly price learning is a high-value problem for sellers. By nature, these auctions are online and produce a very high frequency stream of data. This results in a computational strain that requires algorithms be real-time. Unfortunately, existing methods inherited from the batch setting suffer O($\sqrt t$) time/memory complexity at each update, prohibiting their use. In this paper, we provide the first algorithm for online learning of monopoly prices in online auctions whose update is constant in time and memory.
Efficient Optimistic Exploration in Linear-Quadratic Regulators via Lagrangian Relaxation
Jul 13, 2020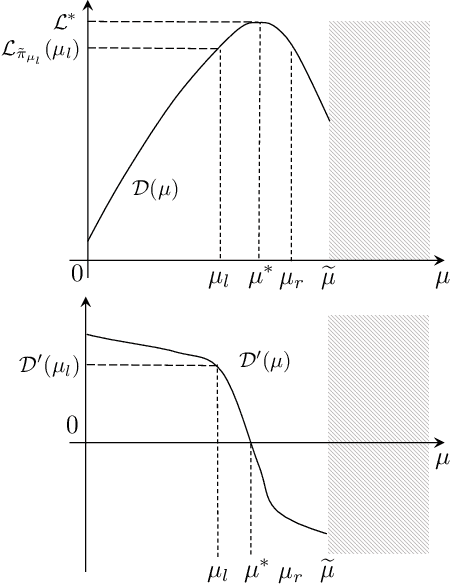

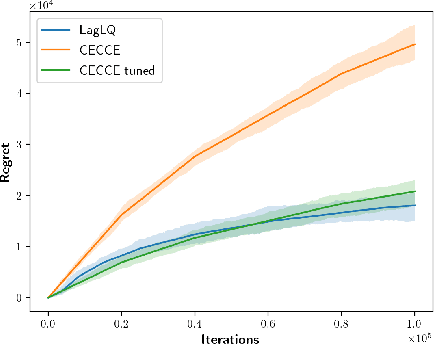

Abstract:We study the exploration-exploitation dilemma in the linear quadratic regulator (LQR) setting. Inspired by the extended value iteration algorithm used in optimistic algorithms for finite MDPs, we propose to relax the optimistic optimization of \ofulq and cast it into a constrained \textit{extended} LQR problem, where an additional control variable implicitly selects the system dynamics within a confidence interval. We then move to the corresponding Lagrangian formulation for which we prove strong duality. As a result, we show that an $\epsilon$-optimistic controller can be computed efficiently by solving at most $O\big(\log(1/\epsilon)\big)$ Riccati equations. Finally, we prove that relaxing the original \ofu problem does not impact the learning performance, thus recovering the $\tilde{O}(\sqrt{T})$ regret of \ofulq. To the best of our knowledge, this is the first computationally efficient confidence-based algorithm for LQR with worst-case optimal regret guarantees.
Improved Optimistic Algorithms for Logistic Bandits
Feb 18, 2020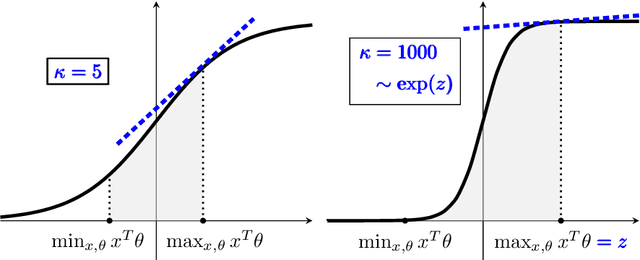

Abstract:The generalized linear bandit framework has attracted a lot of attention in recent years by extending the well-understood linear setting and allowing to model richer reward structures. It notably covers the logistic model, widely used when rewards are binary. For logistic bandits, the frequentist regret guarantees of existing algorithms are $\tilde{\mathcal{O}}(\kappa \sqrt{T})$, where $\kappa$ is a problem-dependent constant. Unfortunately, $\kappa$ can be arbitrarily large as it scales exponentially with the size of the decision set. This may lead to significantly loose regret bounds and poor empirical performance. In this work, we study the logistic bandit with a focus on the prohibitive dependencies introduced by $\kappa$. We propose a new optimistic algorithm based on a finer examination of the non-linearities of the reward function. We show that it enjoys a $\tilde{\mathcal{O}}(\sqrt{T})$ regret with no dependency in $\kappa$, but for a second order term. Our analysis is based on a new tail-inequality for self-normalized martingales, of independent interest.
Thompson Sampling in Non-Episodic Restless Bandits
Oct 12, 2019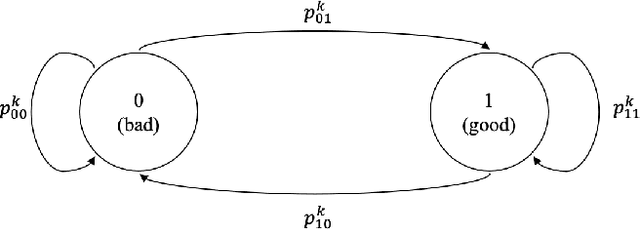
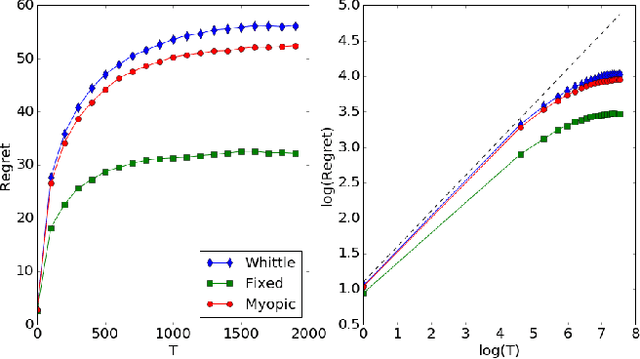
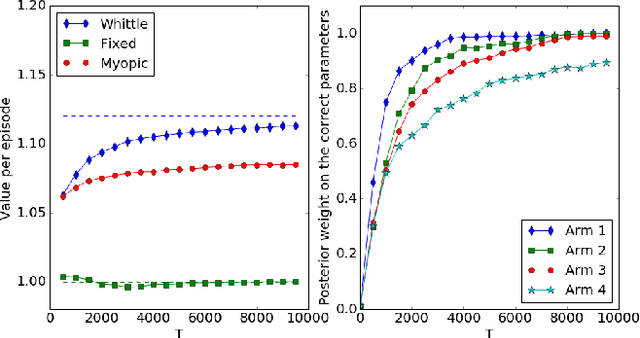
Abstract:Restless bandit problems assume time-varying reward distributions of the arms, which adds flexibility to the model but makes the analysis more challenging. We study learning algorithms over the unknown reward distributions and prove a sub-linear, $O(\sqrt{T}\log T)$, regret bound for a variant of Thompson sampling. Our analysis applies in the infinite time horizon setting, resolving the open question raised by Jung and Tewari (2019) whose analysis is limited to the episodic case. We adopt their policy mapping framework, which allows our algorithm to be efficient and simultaneously keeps the regret meaningful. Our algorithm adapts the TSDE algorithm of Ouyang et al. (2017) in a non-trivial manner to account for the special structure of restless bandits. We test our algorithm on a simulated dynamic channel access problem with several policy mappings, and the empirical regrets agree with the theoretical bound regardless of the choice of the policy mapping.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge