Efficient Optimistic Exploration in Linear-Quadratic Regulators via Lagrangian Relaxation
Paper and Code
Jul 13, 2020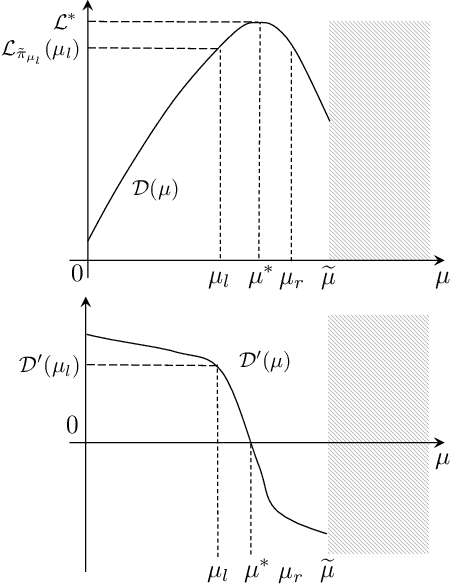

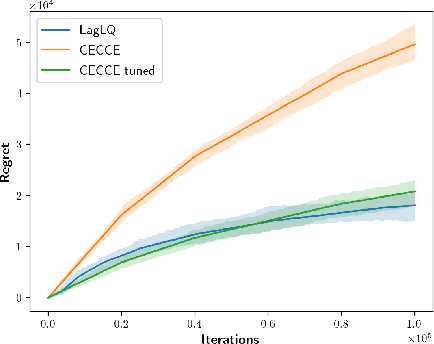

We study the exploration-exploitation dilemma in the linear quadratic regulator (LQR) setting. Inspired by the extended value iteration algorithm used in optimistic algorithms for finite MDPs, we propose to relax the optimistic optimization of \ofulq and cast it into a constrained \textit{extended} LQR problem, where an additional control variable implicitly selects the system dynamics within a confidence interval. We then move to the corresponding Lagrangian formulation for which we prove strong duality. As a result, we show that an $\epsilon$-optimistic controller can be computed efficiently by solving at most $O\big(\log(1/\epsilon)\big)$ Riccati equations. Finally, we prove that relaxing the original \ofu problem does not impact the learning performance, thus recovering the $\tilde{O}(\sqrt{T})$ regret of \ofulq. To the best of our knowledge, this is the first computationally efficient confidence-based algorithm for LQR with worst-case optimal regret guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge