Continuum Transformers Perform In-Context Learning by Operator Gradient Descent

Transformers robustly exhibit the ability to perform in-context learning, whereby their predictive accuracy on a task can increase not by parameter updates but merely with the placement of training samples in their context windows. Recent works have shown that transformers achieve this by implementing gradient descent in their forward passes. Such results, however, are restricted to standard transformer architectures, which handle finite-dimensional inputs. In the space of PDE surrogate modeling, a generalization of transformers to handle infinite-dimensional function inputs, known as "continuum transformers," has been proposed and similarly observed to exhibit in-context learning. Despite impressive empirical performance, such in-context learning has yet to be theoretically characterized. We herein demonstrate that continuum transformers perform in-context operator learning by performing gradient descent in an operator RKHS. We demonstrate this using novel proof strategies that leverage a generalized representer theorem for Hilbert spaces and gradient flows over the space of functionals of a Hilbert space. We additionally show the operator learned in context is the Bayes Optimal Predictor in the infinite depth limit of the transformer. We then provide empirical validations of this optimality result and demonstrate that the parameters under which such gradient descent is performed are recovered through the continuum transformer training.

Offline Constrained Reinforcement Learning under Partial Data Coverage

We study offline constrained reinforcement learning (RL) with general function approximation. We aim to learn a policy from a pre-collected dataset that maximizes the expected discounted cumulative reward for a primary reward signal while ensuring that expected discounted returns for multiple auxiliary reward signals are above predefined thresholds. Existing algorithms either require fully exploratory data, are computationally inefficient, or depend on an additional auxiliary function classes to obtain an $\epsilon$-optimal policy with sample complexity $O(\epsilon^{-2})$. In this paper, we propose an oracle-efficient primal-dual algorithm based on a linear programming (LP) formulation, achieving $O(\epsilon^{-2})$ sample complexity under partial data coverage. By introducing a realizability assumption, our approach ensures that all saddle points of the Lagrangian are optimal, removing the need for regularization that complicated prior analyses. Through Lagrangian decomposition, our method extracts policies without requiring knowledge of the data-generating distribution, enhancing practical applicability.

Operator Learning for Schrödinger Equation: Unitarity, Error Bounds, and Time Generalization

We consider the problem of learning the evolution operator for the time-dependent Schr\"{o}dinger equation, where the Hamiltonian may vary with time. Existing neural network-based surrogates often ignore fundamental properties of the Schr\"{o}dinger equation, such as linearity and unitarity, and lack theoretical guarantees on prediction error or time generalization. To address this, we introduce a linear estimator for the evolution operator that preserves a weak form of unitarity. We establish both upper and lower bounds on the prediction error that hold uniformly over all sufficiently smooth initial wave functions. Additionally, we derive time generalization bounds that quantify how the estimator extrapolates beyond the time points seen during training. Experiments across real-world Hamiltonians -- including hydrogen atoms, ion traps for qubit design, and optical lattices -- show that our estimator achieves relative errors $10^{-2}$ to $10^{-3}$ times smaller than state-of-the-art methods such as the Fourier Neural Operator and DeepONet.

Generator-Mediated Bandits: Thompson Sampling for GenAI-Powered Adaptive Interventions

Recent advances in generative artificial intelligence (GenAI) models have enabled the generation of personalized content that adapts to up-to-date user context. While personalized decision systems are often modeled using bandit formulations, the integration of GenAI introduces new structure into otherwise classical sequential learning problems. In GenAI-powered interventions, the agent selects a query, but the environment experiences a stochastic response drawn from the generative model. Standard bandit methods do not explicitly account for this structure, where actions influence rewards only through stochastic, observed treatments. We introduce generator-mediated bandit-Thompson sampling (GAMBITTS), a bandit approach designed for this action/treatment split, using mobile health interventions with large language model-generated text as a motivating case study. GAMBITTS explicitly models both the treatment and reward generation processes, using information in the delivered treatment to accelerate policy learning relative to standard methods. We establish regret bounds for GAMBITTS by decomposing sources of uncertainty in treatment and reward, identifying conditions where it achieves stronger guarantees than standard bandit approaches. In simulation studies, GAMBITTS consistently outperforms conventional algorithms by leveraging observed treatments to more accurately estimate expected rewards.

On Next-Token Prediction in LLMs: How End Goals Determine the Consistency of Decoding Algorithms

Probabilistic next-token prediction trained using cross-entropy loss is the basis of most large language models. Given a sequence of previous values, next-token prediction assigns a probability to each possible next value in the vocabulary. There are many ways to use next-token prediction to output token sequences. This paper examines a few of these algorithms (greedy, lookahead, random sampling, and temperature-scaled random sampling) and studies their consistency with respect to various goals encoded as loss functions. Although consistency of surrogate losses with respect to a target loss function is a well researched topic, we are the first to study it in the context of LLMs (to the best of our knowledge). We find that, so long as next-token prediction converges to its true probability distribution, random sampling is consistent with outputting sequences that mimic sampling from the true probability distribution. For the other goals, such as minimizing the 0-1 loss on the entire sequence, we show no polynomial-time algorithm is optimal for all probability distributions and all decoding algorithms studied are only optimal for a subset of probability distributions. When analyzing these results, we see that there is a dichotomy created between the goals of information retrieval and creative generation for the decoding algorithms. This shows that choosing the correct decoding algorithm based on the desired goal is extremely important and many of the ones used are lacking theoretical grounding in numerous scenarios.

A Computationally Efficient Algorithm for Infinite-Horizon Average-Reward Linear MDPs

We study reinforcement learning in infinite-horizon average-reward settings with linear MDPs. Previous work addresses this problem by approximating the average-reward setting by discounted setting and employing a value iteration-based algorithm that uses clipping to constrain the span of the value function for improved statistical efficiency. However, the clipping procedure requires computing the minimum of the value function over the entire state space, which is prohibitive since the state space in linear MDP setting can be large or even infinite. In this paper, we introduce a value iteration method with efficient clipping operation that only requires computing the minimum of value functions over the set of states visited by the algorithm. Our algorithm enjoys the same regret bound as the previous work while being computationally efficient, with computational complexity that is independent of the size of the state space.

Operator Learning: A Statistical Perspective

Operator learning has emerged as a powerful tool in scientific computing for approximating mappings between infinite-dimensional function spaces. A primary application of operator learning is the development of surrogate models for the solution operators of partial differential equations (PDEs). These methods can also be used to develop black-box simulators to model system behavior from experimental data, even without a known mathematical model. In this article, we begin by formalizing operator learning as a function-to-function regression problem and review some recent developments in the field. We also discuss PDE-specific operator learning, outlining strategies for incorporating physical and mathematical constraints into architecture design and training processes. Finally, we end by highlighting key future directions such as active data collection and the development of rigorous uncertainty quantification frameworks.

Learning to Partially Defer for Sequences

In the Learning to Defer (L2D) framework, a prediction model can either make a prediction or defer it to an expert, as determined by a rejector. Current L2D methods train the rejector to decide whether to reject the entire prediction, which is not desirable when the model predicts long sequences. We present an L2D setting for sequence outputs where the system can defer specific outputs of the whole model prediction to an expert in an effort to interleave the expert and machine throughout the prediction. We propose two types of model-based post-hoc rejectors for pre-trained predictors: a token-level rejector, which defers specific token predictions to experts with next token prediction capabilities, and a one-time rejector for experts without such abilities, which defers the remaining sequence from a specific point onward. In the experiments, we also empirically demonstrate that such granular deferrals achieve better cost-accuracy tradeoffs than whole deferrals on Traveling salesman solvers and News summarization models.

Who Wrote This? Zero-Shot Statistical Tests for LLM-Generated Text Detection using Finite Sample Concentration Inequalities

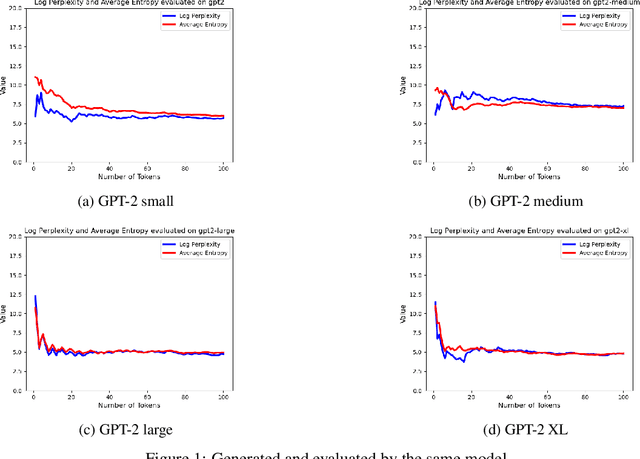
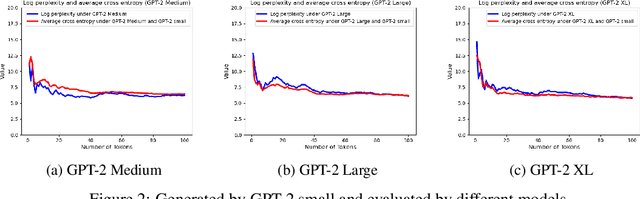
Verifying the provenance of content is crucial to the function of many organizations, e.g., educational institutions, social media platforms, firms, etc. This problem is becoming increasingly difficult as text generated by Large Language Models (LLMs) becomes almost indistinguishable from human-generated content. In addition, many institutions utilize in-house LLMs and want to ensure that external, non-sanctioned LLMs do not produce content within the institution. In this paper, we answer the following question: Given a piece of text, can we identify whether it was produced by LLM $A$ or $B$ (where $B$ can be a human)? We model LLM-generated text as a sequential stochastic process with complete dependence on history and design zero-shot statistical tests to distinguish between (i) the text generated by two different sets of LLMs $A$ (in-house) and $B$ (non-sanctioned) and also (ii) LLM-generated and human-generated texts. We prove that the type I and type II errors for our tests decrease exponentially in the text length. In designing our tests, we derive concentration inequalities on the difference between log-perplexity and the average entropy of the string under $A$. Specifically, for a given string, we demonstrate that if the string is generated by $A$, the log-perplexity of the string under $A$ converges to the average entropy of the string under $A$, except with an exponentially small probability in string length. We also show that if $B$ generates the text, except with an exponentially small probability in string length, the log-perplexity of the string under $A$ converges to the average cross-entropy of $B$ and $A$. Lastly, we present preliminary experimental results to support our theoretical results. By enabling guaranteed (with high probability) finding of the origin of harmful LLM-generated text with arbitrary size, we can help fight misinformation.

Near Optimal Pure Exploration in Logistic Bandits

Bandit algorithms have garnered significant attention due to their practical applications in real-world scenarios. However, beyond simple settings such as multi-arm or linear bandits, optimal algorithms remain scarce. Notably, no optimal solution exists for pure exploration problems in the context of generalized linear model (GLM) bandits. In this paper, we narrow this gap and develop the first track-and-stop algorithm for general pure exploration problems under the logistic bandit called logistic track-and-stop (Log-TS). Log-TS is an efficient algorithm that asymptotically matches an approximation for the instance-specific lower bound of the expected sample complexity up to a logarithmic factor.