Efficient Algorithms for Extreme Bandits

In this paper, we contribute to the Extreme Bandit problem, a variant of Multi-Armed Bandits in which the learner seeks to collect the largest possible reward. We first study the concentration of the maximum of i.i.d random variables under mild assumptions on the tail of the rewards distributions. This analysis motivates the introduction of Quantile of Maxima (QoMax). The properties of QoMax are sufficient to build an Explore-Then-Commit (ETC) strategy, QoMax-ETC, achieving strong asymptotic guarantees despite its simplicity. We then propose and analyze a more adaptive, anytime algorithm, QoMax-SDA, which combines QoMax with a subsampling method recently introduced by Baudry et al. (2021). Both algorithms are more efficient than existing approaches in two aspects (1) they lead to better empirical performance (2) they enjoy a significant reduction of the memory and time complexities.

A/B/n Testing with Control in the Presence of Subpopulations

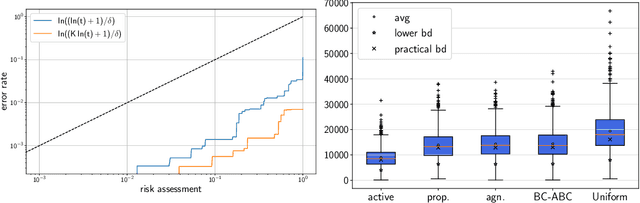
Motivated by A/B/n testing applications, we consider a finite set of distributions (called \emph{arms}), one of which is treated as a \emph{control}. We assume that the population is stratified into homogeneous subpopulations. At every time step, a subpopulation is sampled and an arm is chosen: the resulting observation is an independent draw from the arm conditioned on the subpopulation. The quality of each arm is assessed through a weighted combination of its subpopulation means. We propose a strategy for sequentially choosing one arm per time step so as to discover as fast as possible which arms, if any, have higher weighted expectation than the control. This strategy is shown to be asymptotically optimal in the following sense: if $\tau_\delta$ is the first time when the strategy ensures that it is able to output the correct answer with probability at least $1-\delta$, then $\mathbb{E}[\tau_\delta]$ grows linearly with $\log(1/\delta)$ at the exact optimal rate. This rate is identified in the paper in three different settings: (1) when the experimenter does not observe the subpopulation information, (2) when the subpopulation of each sample is observed but not chosen, and (3) when the experimenter can select the subpopulation from which each response is sampled. We illustrate the efficiency of the proposed strategy with numerical simulations on synthetic and real data collected from an A/B/n experiment.

On Limited-Memory Subsampling Strategies for Bandits

There has been a recent surge of interest in nonparametric bandit algorithms based on subsampling. One drawback however of these approaches is the additional complexity required by random subsampling and the storage of the full history of rewards. Our first contribution is to show that a simple deterministic subsampling rule, proposed in the recent work of Baudry et al. (2020) under the name of ''last-block subsampling'', is asymptotically optimal in one-parameter exponential families. In addition, we prove that these guarantees also hold when limiting the algorithm memory to a polylogarithmic function of the time horizon. These findings open up new perspectives, in particular for non-stationary scenarios in which the arm distributions evolve over time. We propose a variant of the algorithm in which only the most recent observations are used for subsampling, achieving optimal regret guarantees under the assumption of a known number of abrupt changes. Extensive numerical simulations highlight the merits of this approach, particularly when the changes are not only affecting the means of the rewards.

Regret Bounds for Generalized Linear Bandits under Parameter Drift

Generalized Linear Bandits (GLBs) are powerful extensions to the Linear Bandit (LB) setting, broadening the benefits of reward parametrization beyond linearity. In this paper we study GLBs in non-stationary environments, characterized by a general metric of non-stationarity known as the variation-budget or \emph{parameter-drift}, denoted $B_T$. While previous attempts have been made to extend LB algorithms to this setting, they overlook a salient feature of GLBs which flaws their results. In this work, we introduce a new algorithm that addresses this difficulty. We prove that under a geometric assumption on the action set, our approach enjoys a $\tilde{\mathcal{O}}(B_T^{1/3}T^{2/3})$ regret bound. In the general case, we show that it suffers at most a $\tilde{\mathcal{O}}(B_T^{1/5}T^{4/5})$ regret. At the core of our contribution is a generalization of the projection step introduced in Filippi et al. (2010), adapted to the non-stationary nature of the problem. Our analysis sheds light on central mechanisms inherited from the setting by explicitly splitting the treatment of the learning and tracking aspects of the problem.

Self-Concordant Analysis of Generalized Linear Bandits with Forgetting

Contextual sequential decision problems with categorical or numerical observations are ubiquitous and Generalized Linear Bandits (GLB) offer a solid theoretical framework to address them. In contrast to the case of linear bandits, existing algorithms for GLB have two drawbacks undermining their applicability. First, they rely on excessively pessimistic concentration bounds due to the non-linear nature of the model. Second, they require either non-convex projection steps or burn-in phases to enforce boundedness of the estimators. Both of these issues are worsened when considering non-stationary models, in which the GLB parameter may vary with time. In this work, we focus on self-concordant GLB (which include logistic and Poisson regression) with forgetting achieved either by the use of a sliding window or exponential weights. We propose a novel confidence-based algorithm for the maximum-likehood estimator with forgetting and analyze its perfomance in abruptly changing environments. These results as well as the accompanying numerical simulations highlight the potential of the proposed approach to address non-stationarity in GLB.

Algorithms for Non-Stationary Generalized Linear Bandits

The statistical framework of Generalized Linear Models (GLM) can be applied to sequential problems involving categorical or ordinal rewards associated, for instance, with clicks, likes or ratings. In the example of binary rewards, logistic regression is well-known to be preferable to the use of standard linear modeling. Previous works have shown how to deal with GLMs in contextual online learning with bandit feedback when the environment is assumed to be stationary. In this paper, we relax this latter assumption and propose two upper confidence bound based algorithms that make use of either a sliding window or a discounted maximum-likelihood estimator. We provide theoretical guarantees on the behavior of these algorithms for general context sequences and in the presence of abrupt changes. These results take the form of high probability upper bounds for the dynamic regret that are of order d^2/3 G^1/3 T^2/3 , where d, T and G are respectively the dimension of the unknown parameter, the number of rounds and the number of breakpoints up to time T. The empirical performance of the algorithms is illustrated in simulated environments.

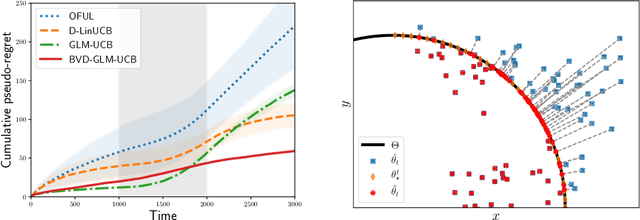
Weighted Linear Bandits for Non-Stationary Environments

We consider a stochastic linear bandit model in which the available actions correspond to arbitrary context vectors whose associated rewards follow a non-stationary linear regression model. In this setting, the unknown regression parameter is allowed to vary in time. To address this problem, we propose D-LinUCB, a novel optimistic algorithm based on discounted linear regression, where exponential weights are used to smoothly forget the past. This involves studying the deviations of the sequential weighted least-squares estimator under generic assumptions. As a by-product, we obtain novel deviation results that can be used beyond non-stationary environments. We provide theoretical guarantees on the behavior of D-LinUCB in both slowly-varying and abruptly-changing environments. We obtain an upper bound on the dynamic regret that is of order $d^{2/3} B_T^{1/3}T^{2/3}$, where $B_T$ is a measure of non-stationarity (d and T being, respectively, dimension and horizon). This rate is known to be optimal. We also illustrate the empirical performance of D-LinUCB and compare it with recently proposed alternatives in simulated environments.