Jointly Efficient and Optimal Algorithms for Logistic Bandits

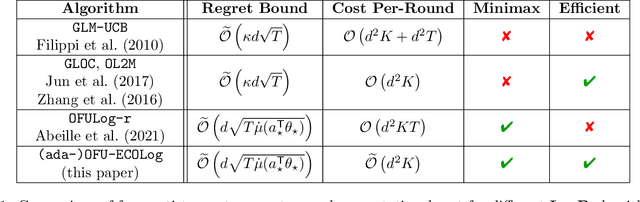
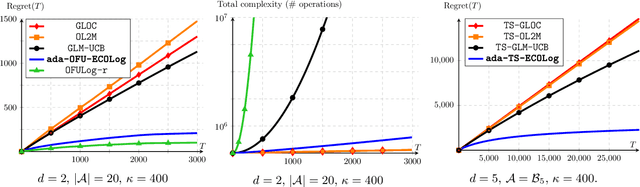
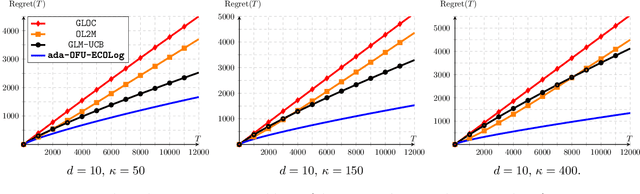
Logistic Bandits have recently undergone careful scrutiny by virtue of their combined theoretical and practical relevance. This research effort delivered statistically efficient algorithms, improving the regret of previous strategies by exponentially large factors. Such algorithms are however strikingly costly as they require $\Omega(t)$ operations at each round. On the other hand, a different line of research focused on computational efficiency ($\mathcal{O}(1)$ per-round cost), but at the cost of letting go of the aforementioned exponential improvements. Obtaining the best of both world is unfortunately not a matter of marrying both approaches. Instead we introduce a new learning procedure for Logistic Bandits. It yields confidence sets which sufficient statistics can be easily maintained online without sacrificing statistical tightness. Combined with efficient planning mechanisms we design fast algorithms which regret performance still match the problem-dependent lower-bound of Abeille et al. (2021). To the best of our knowledge, those are the first Logistic Bandit algorithms that simultaneously enjoy statistical and computational efficiency.

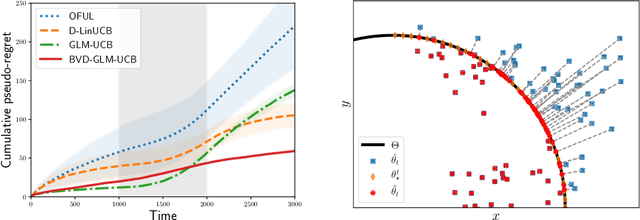
Regret Bounds for Generalized Linear Bandits under Parameter Drift

Generalized Linear Bandits (GLBs) are powerful extensions to the Linear Bandit (LB) setting, broadening the benefits of reward parametrization beyond linearity. In this paper we study GLBs in non-stationary environments, characterized by a general metric of non-stationarity known as the variation-budget or \emph{parameter-drift}, denoted $B_T$. While previous attempts have been made to extend LB algorithms to this setting, they overlook a salient feature of GLBs which flaws their results. In this work, we introduce a new algorithm that addresses this difficulty. We prove that under a geometric assumption on the action set, our approach enjoys a $\tilde{\mathcal{O}}(B_T^{1/3}T^{2/3})$ regret bound. In the general case, we show that it suffers at most a $\tilde{\mathcal{O}}(B_T^{1/5}T^{4/5})$ regret. At the core of our contribution is a generalization of the projection step introduced in Filippi et al. (2010), adapted to the non-stationary nature of the problem. Our analysis sheds light on central mechanisms inherited from the setting by explicitly splitting the treatment of the learning and tracking aspects of the problem.

Improving Offline Contextual Bandits with Distributional Robustness

This paper extends the Distributionally Robust Optimization (DRO) approach for offline contextual bandits. Specifically, we leverage this framework to introduce a convex reformulation of the Counterfactual Risk Minimization principle. Besides relying on convex programs, our approach is compatible with stochastic optimization, and can therefore be readily adapted tothe large data regime. Our approach relies on the construction of asymptotic confidence intervals for offline contextual bandits through the DRO framework. By leveraging known asymptotic results of robust estimators, we also show how to automatically calibrate such confidence intervals, which in turn removes the burden of hyper-parameter selection for policy optimization. We present preliminary empirical results supporting the effectiveness of our approach.

Self-Concordant Analysis of Generalized Linear Bandits with Forgetting

Contextual sequential decision problems with categorical or numerical observations are ubiquitous and Generalized Linear Bandits (GLB) offer a solid theoretical framework to address them. In contrast to the case of linear bandits, existing algorithms for GLB have two drawbacks undermining their applicability. First, they rely on excessively pessimistic concentration bounds due to the non-linear nature of the model. Second, they require either non-convex projection steps or burn-in phases to enforce boundedness of the estimators. Both of these issues are worsened when considering non-stationary models, in which the GLB parameter may vary with time. In this work, we focus on self-concordant GLB (which include logistic and Poisson regression) with forgetting achieved either by the use of a sliding window or exponential weights. We propose a novel confidence-based algorithm for the maximum-likehood estimator with forgetting and analyze its perfomance in abruptly changing environments. These results as well as the accompanying numerical simulations highlight the potential of the proposed approach to address non-stationarity in GLB.

Instance-Wise Minimax-Optimal Algorithms for Logistic Bandits

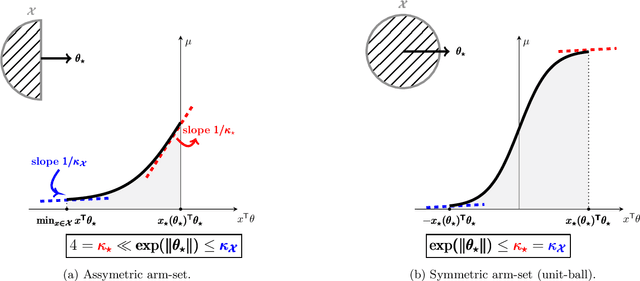
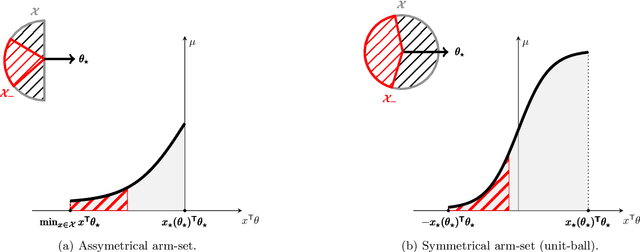
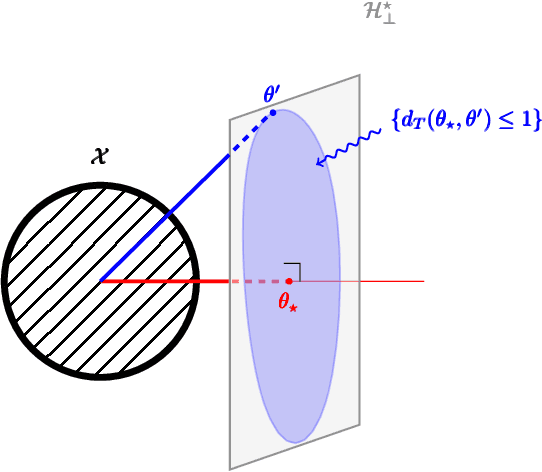
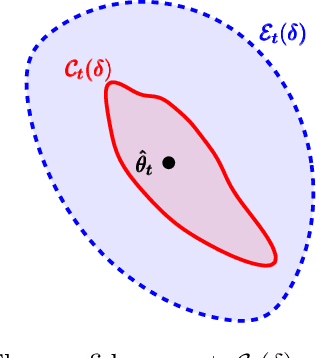
Logistic Bandits have recently attracted substantial attention, by providing an uncluttered yet challenging framework for understanding the impact of non-linearity in parametrized bandits. It was shown by Faury et al. (2020) that the learning-theoretic difficulties of Logistic Bandits can be embodied by a large (sometimes prohibitively) problem-dependent constant $\kappa$, characterizing the magnitude of the reward's non-linearity. In this paper we introduce a novel algorithm for which we provide a refined analysis. This allows for a better characterization of the effect of non-linearity and yields improved problem-dependent guarantees. In most favorable cases this leads to a regret upper-bound scaling as $\tilde{\mathcal{O}}(d\sqrt{T/\kappa})$, which dramatically improves over the $\tilde{\mathcal{O}}(d\sqrt{T}+\kappa)$ state-of-the-art guarantees. We prove that this rate is minimax-optimal by deriving a $\Omega(d\sqrt{T/\kappa})$ problem-dependent lower-bound. Our analysis identifies two regimes (permanent and transitory) of the regret, which ultimately re-conciliates Faury et al. (2020) with the Bayesian approach of Dong et al. (2019). In contrast to previous works, we find that in the permanent regime non-linearity can dramatically ease the exploration-exploitation trade-off. While it also impacts the length of the transitory phase in a problem-dependent fashion, we show that this impact is mild in most reasonable configurations.

Improved Optimistic Algorithms for Logistic Bandits

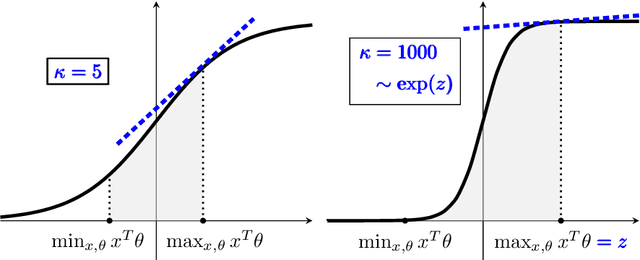
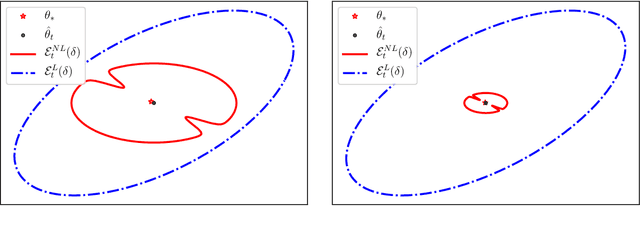
The generalized linear bandit framework has attracted a lot of attention in recent years by extending the well-understood linear setting and allowing to model richer reward structures. It notably covers the logistic model, widely used when rewards are binary. For logistic bandits, the frequentist regret guarantees of existing algorithms are $\tilde{\mathcal{O}}(\kappa \sqrt{T})$, where $\kappa$ is a problem-dependent constant. Unfortunately, $\kappa$ can be arbitrarily large as it scales exponentially with the size of the decision set. This may lead to significantly loose regret bounds and poor empirical performance. In this work, we study the logistic bandit with a focus on the prohibitive dependencies introduced by $\kappa$. We propose a new optimistic algorithm based on a finer examination of the non-linearities of the reward function. We show that it enjoys a $\tilde{\mathcal{O}}(\sqrt{T})$ regret with no dependency in $\kappa$, but for a second order term. Our analysis is based on a new tail-inequality for self-normalized martingales, of independent interest.

Distributionally Robust Counterfactual Risk Minimization

This manuscript introduces the idea of using Distributionally Robust Optimization (DRO) for the Counterfactual Risk Minimization (CRM) problem. Tapping into a rich existing literature, we show that DRO is a principled tool for counterfactual decision making. We also show that well-established solutions to the CRM problem like sample variance penalization schemes are special instances of a more general DRO problem. In this unifying framework, a variety of distributionally robust counterfactual risk estimators can be constructed using various probability distances and divergences as uncertainty measures. We propose the use of Kullback-Leibler divergence as an alternative way to model uncertainty in CRM and derive a new robust counterfactual objective. In our experiments, we show that this approach outperforms the state-of-the-art on four benchmark datasets, validating the relevance of using other uncertainty measures in practical applications.

Improving Evolutionary Strategies with Generative Neural Networks

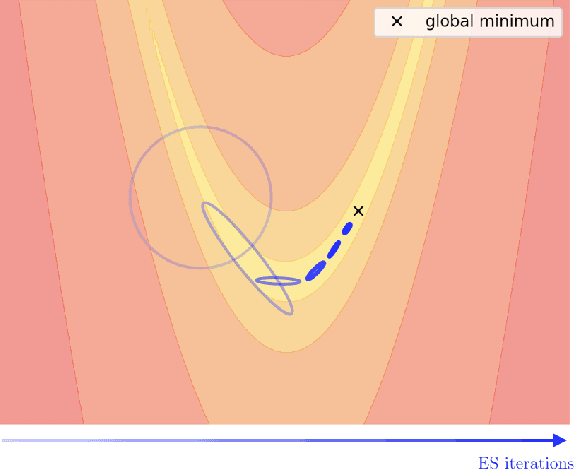
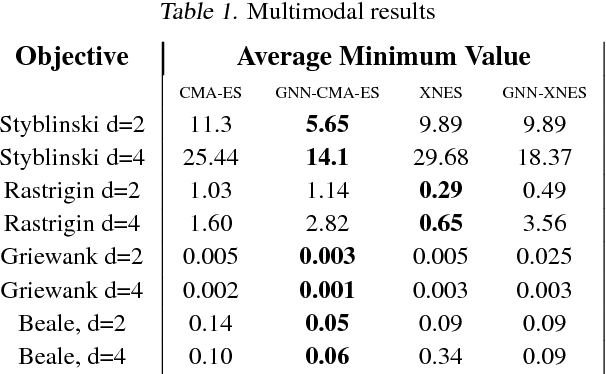
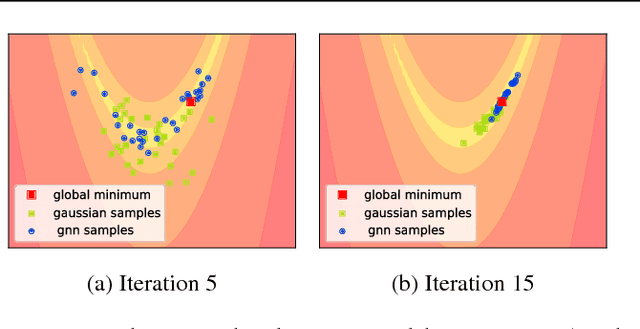
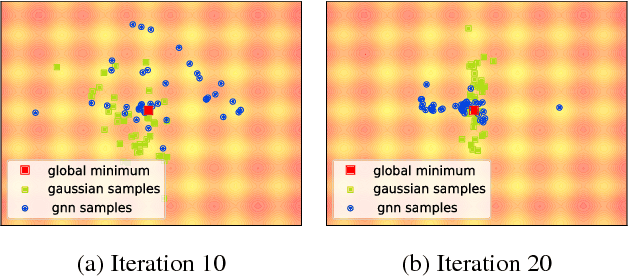
Evolutionary Strategies (ES) are a popular family of black-box zeroth-order optimization algorithms which rely on search distributions to efficiently optimize a large variety of objective functions. This paper investigates the potential benefits of using highly flexible search distributions in classical ES algorithms, in contrast to standard ones (typically Gaussians). We model such distributions with Generative Neural Networks (GNNs) and introduce a new training algorithm that leverages their expressiveness to accelerate the ES procedure. We show that this tailored algorithm can readily incorporate existing ES algorithms, and outperforms the state-of-the-art on diverse objective functions.

Neural Generative Models for Global Optimization with Gradients

The aim of global optimization is to find the global optimum of arbitrary classes of functions, possibly highly multimodal ones. In this paper we focus on the subproblem of global optimization for differentiable functions and we propose an Evolutionary Search-inspired solution where we model point search distributions via Generative Neural Networks. This approach enables us to model diverse and complex search distributions based on which we can efficiently explore complicated objective landscapes. In our experiments we show the practical superiority of our algorithm versus classical Evolutionary Search and gradient-based solutions on a benchmark set of multimodal functions, and demonstrate how it can be used to accelerate Bayesian Optimization with Gaussian Processes.

Rover Descent: Learning to optimize by learning to navigate on prototypical loss surfaces

Learning to optimize - the idea that we can learn from data algorithms that optimize a numerical criterion - has recently been at the heart of a growing number of research efforts. One of the most challenging issues within this approach is to learn a policy that is able to optimize over classes of functions that are fairly different from the ones that it was trained on. We propose a novel way of framing learning to optimize as a problem of learning a good navigation policy on a partially observable loss surface. To this end, we develop Rover Descent, a solution that allows us to learn a fairly broad optimization policy from training on a small set of prototypical two-dimensional surfaces that encompasses the classically hard cases such as valleys, plateaus, cliffs and saddles and by using strictly zero-order information. We show that, without having access to gradient or curvature information, we achieve state-of-the-art convergence speed on optimization problems not presented at training time such as the Rosenbrock function and other hard cases in two dimensions. We extend our framework to optimize over high dimensional landscapes, while still handling only two-dimensional local landscape information and show good preliminary results.