Elvis Dohmatob
PARIETAL
Why Less is More (Sometimes): A Theory of Data Curation
Nov 05, 2025



Abstract:This paper introduces a theoretical framework to resolve a central paradox in modern machine learning: When is it better to use less data? This question has become critical as classical scaling laws suggesting ``more is more'' (Sun et al., 2025) are challenged by methods like LIMO (``less is more'') and s1 (Ye et al., 2025; Muenighoff et al., 2025), which achieve superior performance with small, aggressively curated datasets. Here, we study data curation strategies where an imperfect oracle selects the training examples according to their difficulty and correctness. Our results provide exact scaling law curves for test error under both label-agnostic and label-aware curation rules, revealing when and why keeping only a subset of data can improve generalization. In contrast to classical scaling laws, we show that under certain conditions, small curated datasets can outperform full datasets, and we provide analytical conditions for this by deriving precise phase transition curves tied to data size and quality. We validate these theoretical claims with empirical results on ImageNet, confirming our predictions about when curation improves accuracy and can even mitigate model collapse. Furthermore, our framework provides a principled explanation for the contradictory curation strategies recently observed in LLM mathematical reasoning.
Egalitarian Gradient Descent: A Simple Approach to Accelerated Grokking
Oct 06, 2025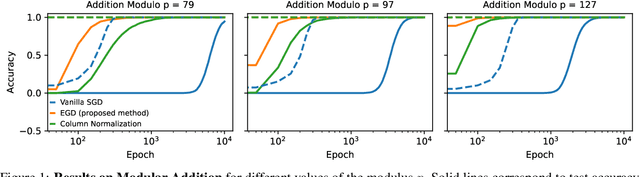
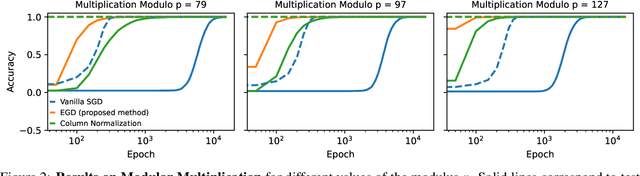
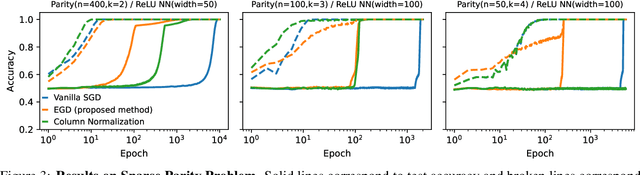
Abstract:Grokking is the phenomenon whereby, unlike the training performance, which peaks early in the training process, the test/generalization performance of a model stagnates over arbitrarily many epochs and then suddenly jumps to usually close to perfect levels. In practice, it is desirable to reduce the length of such plateaus, that is to make the learning process "grok" faster. In this work, we provide new insights into grokking. First, we show both empirically and theoretically that grokking can be induced by asymmetric speeds of (stochastic) gradient descent, along different principal (i.e singular directions) of the gradients. We then propose a simple modification that normalizes the gradients so that dynamics along all the principal directions evolves at exactly the same speed. Then, we establish that this modified method, which we call egalitarian gradient descent (EGD) and can be seen as a carefully modified form of natural gradient descent, groks much faster. In fact, in some cases the stagnation is completely removed. Finally, we empirically show that on classical arithmetic problems such as modular addition and sparse parity problem which this stagnation has been widely observed and intensively studied, that our proposed method eliminates the plateaus.
auto-fpt: Automating Free Probability Theory Calculations for Machine Learning Theory
Apr 14, 2025Abstract:A large part of modern machine learning theory often involves computing the high-dimensional expected trace of a rational expression of large rectangular random matrices. To symbolically compute such quantities using free probability theory, we introduce auto-fpt, a lightweight Python and SymPy-based tool that can automatically produce a reduced system of fixed-point equations which can be solved for the quantities of interest, and effectively constitutes a theory. We overview the algorithmic ideas underlying auto-fpt and its applications to various interesting problems, such as the high-dimensional error of linearized feed-forward neural networks, recovering well-known results. We hope that auto-fpt streamlines the majority of calculations involved in high-dimensional analysis, while helping the machine learning community reproduce known and uncover new phenomena.
Improving the Scaling Laws of Synthetic Data with Deliberate Practice
Feb 21, 2025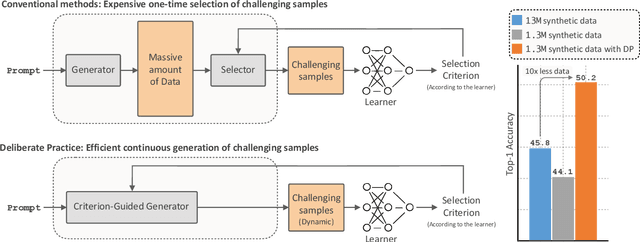
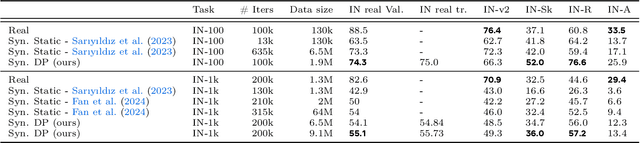
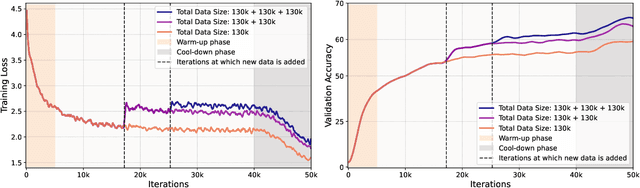

Abstract:Inspired by the principle of deliberate practice in human learning, we propose Deliberate Practice for Synthetic Data Generation (DP), a novel framework that improves sample efficiency through dynamic synthetic data generation. Prior work has shown that scaling synthetic data is inherently challenging, as naively adding new data leads to diminishing returns. To address this, pruning has been identified as a key mechanism for improving scaling, enabling models to focus on the most informative synthetic samples. Rather than generating a large dataset and pruning it afterward, DP efficiently approximates the direct generation of informative samples. We theoretically show how training on challenging, informative examples improves scaling laws and empirically validate that DP achieves better scaling performance with significantly fewer training samples and iterations. On ImageNet-100, DP generates 3.4x fewer samples and requires six times fewer iterations, while on ImageNet-1k, it generates 8x fewer samples with a 30 percent reduction in iterations, all while achieving superior performance compared to prior work.
The Pitfalls of Memorization: When Memorization Hurts Generalization
Dec 10, 2024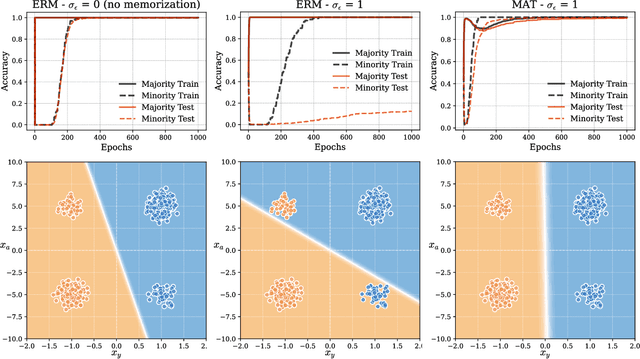

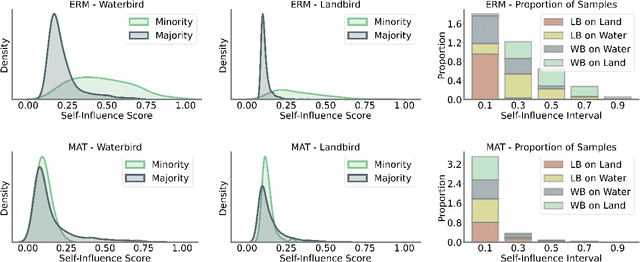

Abstract:Neural networks often learn simple explanations that fit the majority of the data while memorizing exceptions that deviate from these explanations.This behavior leads to poor generalization when the learned explanations rely on spurious correlations. In this work, we formalize the interplay between memorization and generalization, showing that spurious correlations would particularly lead to poor generalization when are combined with memorization. Memorization can reduce training loss to zero, leaving no incentive to learn robust, generalizable patterns. To address this, we propose memorization-aware training (MAT), which uses held-out predictions as a signal of memorization to shift a model's logits. MAT encourages learning robust patterns invariant across distributions, improving generalization under distribution shifts.
Strong Model Collapse
Oct 07, 2024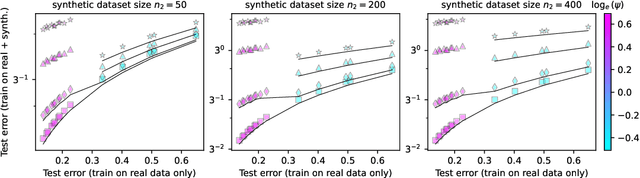

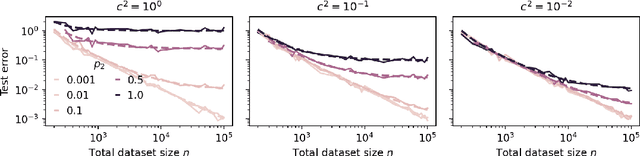

Abstract:Within the scaling laws paradigm, which underpins the training of large neural networks like ChatGPT and Llama, we consider a supervised regression setting and establish the existance of a strong form of the model collapse phenomenon, a critical performance degradation due to synthetic data in the training corpus. Our results show that even the smallest fraction of synthetic data (e.g., as little as 1\% of the total training dataset) can still lead to model collapse: larger and larger training sets do not enhance performance. We further investigate whether increasing model size, an approach aligned with current trends in training large language models, exacerbates or mitigates model collapse. In a simplified regime where neural networks are approximated via random projections of tunable size, we both theoretically and empirically show that larger models can amplify model collapse. Interestingly, our theory also indicates that, beyond the interpolation threshold (which can be extremely high for very large datasets), larger models may mitigate the collapse, although they do not entirely prevent it. Our theoretical findings are empirically verified through experiments on language models and feed-forward neural networks for images.
Beyond Model Collapse: Scaling Up with Synthesized Data Requires Reinforcement
Jun 11, 2024



Abstract:Synthesized data from generative models is increasingly considered as an alternative to human-annotated data for fine-tuning Large Language Models. This raises concerns about model collapse: a drop in performance of models fine-tuned on generated data. Considering that it is easier for both humans and machines to tell between good and bad examples than to generate high-quality samples, we investigate the use of feedback on synthesized data to prevent model collapse. We derive theoretical conditions under which a Gaussian mixture classification model can achieve asymptotically optimal performance when trained on feedback-augmented synthesized data, and provide supporting simulations for finite regimes. We illustrate our theoretical predictions on two practical problems: computing matrix eigenvalues with transformers and news summarization with large language models, which both undergo model collapse when trained on model-generated data. We show that training from feedback-augmented synthesized data, either by pruning incorrect predictions or by selecting the best of several guesses, can prevent model collapse, validating popular approaches like RLHF.
Model Collapse Demystified: The Case of Regression
Feb 12, 2024Abstract:In the era of large language models like ChatGPT, the phenomenon of "model collapse" refers to the situation whereby as a model is trained recursively on data generated from previous generations of itself over time, its performance degrades until the model eventually becomes completely useless, i.e the model collapses. In this work, we study this phenomenon in the simplified setting of kernel regression and obtain results which show a clear crossover between where the model can cope with fake data, and a regime where the model's performance completely collapses. Under polynomial decaying spectral and source conditions, we obtain modified scaling laws which exhibit new crossover phenomena from fast to slow rates. We also propose a simple strategy based on adaptive regularization to mitigate model collapse. Our theoretical results are validated with experiments.
A Tale of Tails: Model Collapse as a Change of Scaling Laws
Feb 10, 2024



Abstract:As AI model size grows, neural scaling laws have become a crucial tool to predict the improvements of large models when increasing capacity and the size of original (human or natural) training data. Yet, the widespread use of popular models means that the ecosystem of online data and text will co-evolve to progressively contain increased amounts of synthesized data. In this paper we ask: How will the scaling laws change in the inevitable regime where synthetic data makes its way into the training corpus? Will future models, still improve, or be doomed to degenerate up to total (model) collapse? We develop a theoretical framework of model collapse through the lens of scaling laws. We discover a wide range of decay phenomena, analyzing loss of scaling, shifted scaling with number of generations, the ''un-learning" of skills, and grokking when mixing human and synthesized data. Our theory is validated by large-scale experiments with a transformer on an arithmetic task and text generation using the large language model Llama2.
Scaling Laws for Associative Memories
Oct 04, 2023Abstract:Learning arguably involves the discovery and memorization of abstract rules. The aim of this paper is to study associative memory mechanisms. Our model is based on high-dimensional matrices consisting of outer products of embeddings, which relates to the inner layers of transformer language models. We derive precise scaling laws with respect to sample size and parameter size, and discuss the statistical efficiency of different estimators, including optimization-based algorithms. We provide extensive numerical experiments to validate and interpret theoretical results, including fine-grained visualizations of the stored memory associations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge