Towards Efficient Optimizer Design for LLM via Structured Fisher Approximation with a Low-Rank Extension

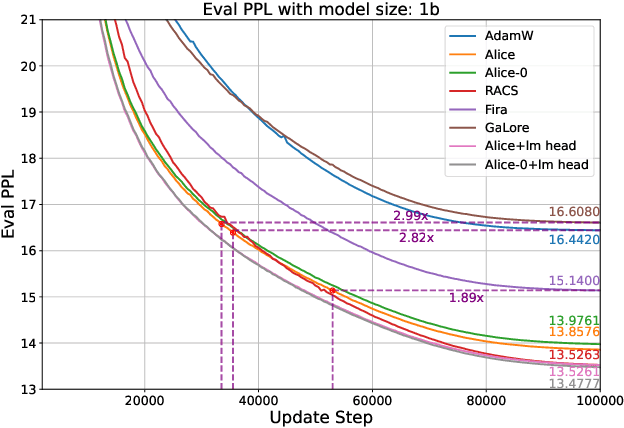
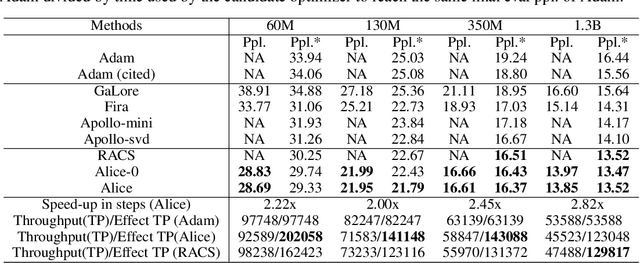
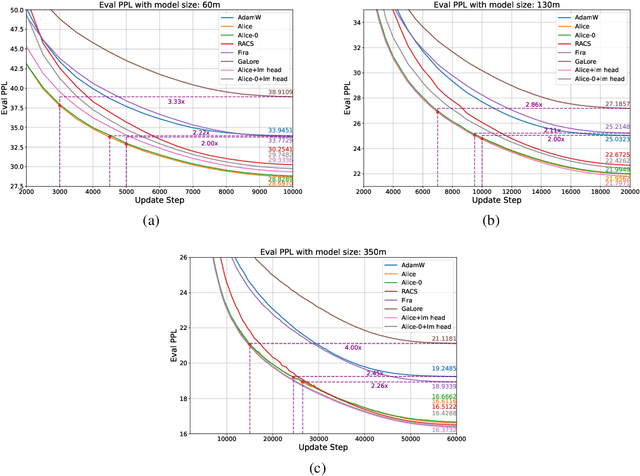
Designing efficient optimizers for large language models (LLMs) with low-memory requirements and fast convergence is an important and challenging problem. This paper makes a step towards the systematic design of such optimizers through the lens of structured Fisher information matrix (FIM) approximation. We show that many state-of-the-art efficient optimizers can be viewed as solutions to FIM approximation (under the Frobenius norm) with specific structural assumptions. Building on these insights, we propose two design recommendations of practical efficient optimizers for LLMs, involving the careful selection of structural assumptions to balance generality and efficiency, and enhancing memory efficiency of optimizers with general structures through a novel low-rank extension framework. We demonstrate how to use each design approach by deriving new memory-efficient optimizers: Row and Column Scaled SGD (RACS) and Adaptive low-dimensional subspace estimation (Alice). Experiments on LLaMA pre-training (up to 1B parameters) validate the effectiveness, showing faster and better convergence than existing memory-efficient baselines and Adam with little memory overhead. Notably, Alice achieves better than 2x faster convergence over Adam, while RACS delivers strong performance on the 1B model with SGD-like memory.

Gradient Multi-Normalization for Stateless and Scalable LLM Training

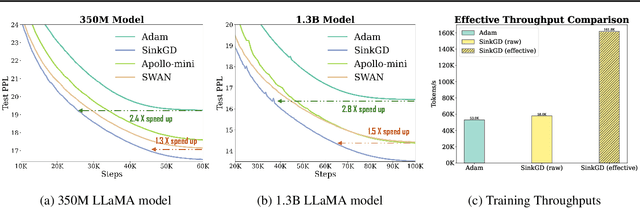
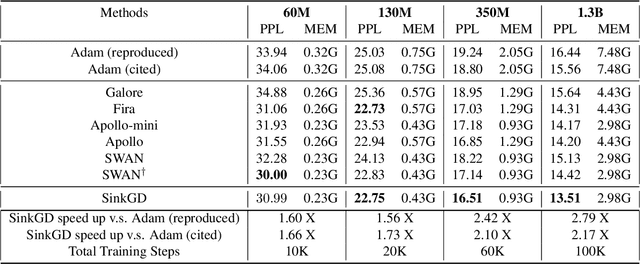
Training large language models (LLMs) typically relies on adaptive optimizers like Adam (Kingma & Ba, 2015) which store additional state information to accelerate convergence but incur significant memory overhead. Recent efforts, such as SWAN (Ma et al., 2024) address this by eliminating the need for optimizer states while achieving performance comparable to Adam via a multi-step preprocessing procedure applied to instantaneous gradients. Motivated by the success of SWAN, we introduce a novel framework for designing stateless optimizers that normalizes stochastic gradients according to multiple norms. To achieve this, we propose a simple alternating scheme to enforce the normalization of gradients w.r.t these norms. We show that our procedure can produce, up to an arbitrary precision, a fixed-point of the problem, and that SWAN is a particular instance of our approach with carefully chosen norms, providing a deeper understanding of its design. However, SWAN's computationally expensive whitening/orthogonalization step limit its practicality for large LMs. Using our principled perspective, we develop of a more efficient, scalable, and practical stateless optimizer. Our algorithm relaxes the properties of SWAN, significantly reducing its computational cost while retaining its memory efficiency, making it applicable to training large-scale models. Experiments on pre-training LLaMA models with up to 1 billion parameters demonstrate a 3X speedup over Adam with significantly reduced memory requirements, outperforming other memory-efficient baselines.

SWAN: SGD with Normalization and Whitening Enables Stateless LLM Training

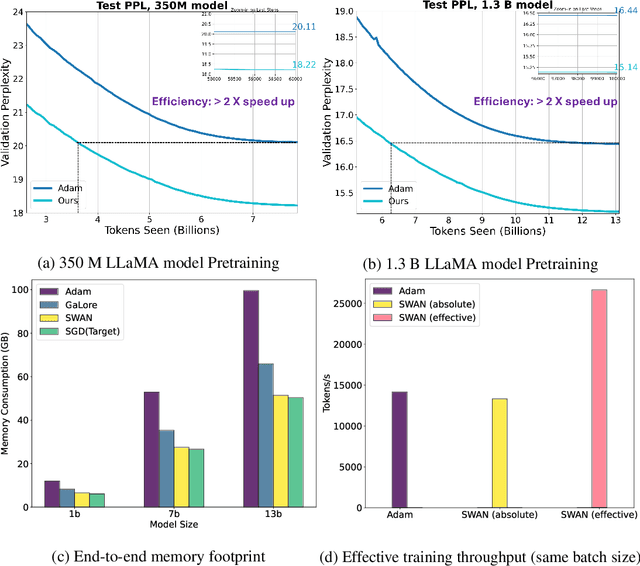
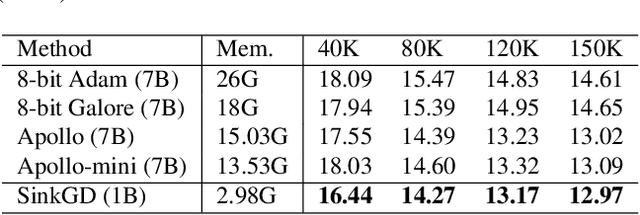
Adaptive optimizers such as Adam (Kingma & Ba, 2015) have been central to the success of large language models. However, they often require to maintain optimizer states throughout training, which can result in memory requirements several times greater than the model footprint. This overhead imposes constraints on scalability and computational efficiency. Stochastic Gradient Descent (SGD), in contrast, is a stateless optimizer, as it does not track state variables during training. Consequently, it achieves optimal memory efficiency. However, its capability in LLM training is limited (Zhao et al., 2024b). In this work, we show that pre-processing SGD in a stateless manner can achieve the same performance as the Adam optimizer for LLM training, while drastically reducing the memory cost. Specifically, we propose to pre-process the instantaneous stochastic gradients using normalization and whitening. We show that normalization stabilizes gradient distributions, and whitening counteracts the local curvature of the loss landscape. This results in SWAN (SGD with Whitening And Normalization), a stochastic optimizer that eliminates the need to store any optimizer states. Empirically, SWAN has the same memory footprint as SGD, achieving $\approx 50\%$ reduction on total end-to-end memory compared to Adam. In language modeling tasks, SWAN demonstrates comparable or even better performance than Adam: when pre-training the LLaMA model with 350M and 1.3B parameters, SWAN achieves a 2x speedup by reaching the same evaluation perplexity using half as many tokens.

SWAN: Preprocessing SGD Enables Adam-Level Performance On LLM Training With Significant Memory Reduction

Adaptive optimizers such as Adam (Kingma & Ba, 2015) have been central to the success of large language models. However, they maintain additional moving average states throughout training, which results in memory requirements several times greater than the model. This overhead imposes constraints on scalability and computational efficiency. On the other hand, while stochastic gradient descent (SGD) is optimal in terms of memory efficiency, their capability in LLM training is limited (Zhao et al., 2024b). To address this dilemma, we show that pre-processing SGD is sufficient to reach Adam-level performance on LLMs. Specifically, we propose to preprocess the instantaneous stochastic gradients with two simple operators: $\mathtt{GradNorm}$ and $\mathtt{GradWhitening}$. $\mathtt{GradNorm}$ stabilizes gradient distributions, and $\mathtt{GradWhitening}$ counteracts the local curvature of the loss landscape, respectively. This results in SWAN (SGD with Whitening And Normalization), a stochastic optimizer that eliminates the need to store any accumulative state variables. Empirically, SWAN has the same memory footprint as SGD, achieving $\approx 50\%$ reduction on total end-to-end memory compared to Adam. In language modeling tasks, SWAN demonstrates the same or even a substantial improvement over Adam. Specifically, when pre-training the LLaMa model with 350M and 1.3B parameters, SWAN achieves a 2x speedup by reaching the same evaluation perplexity in less than half tokens seen.

Low-Rank Correction for Quantized LLMs

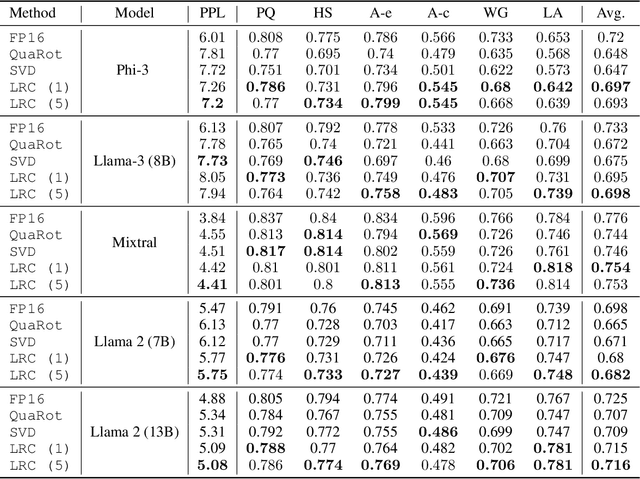
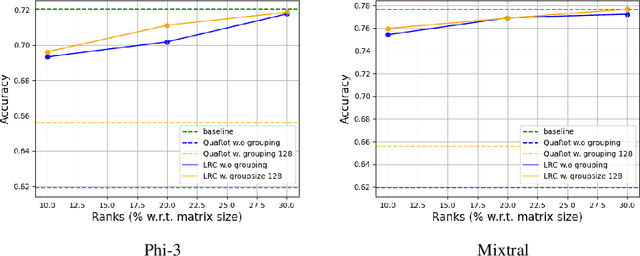
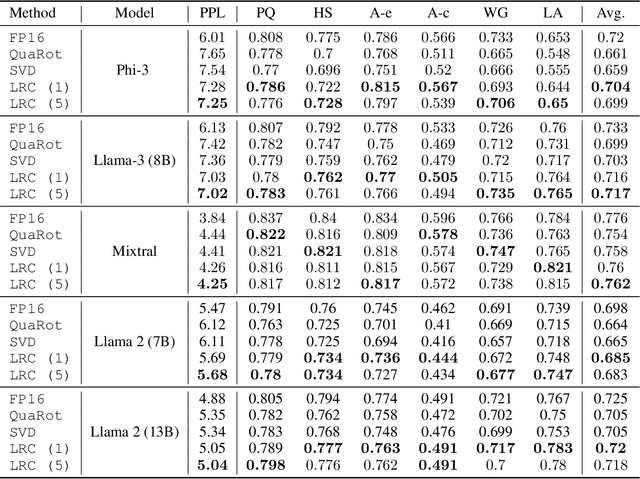
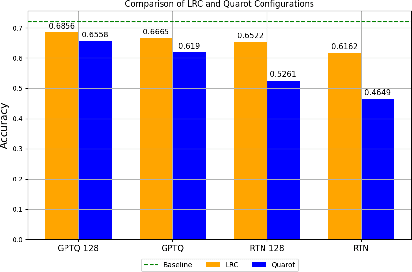
We consider the problem of model compression for Large Language Models (LLMs) at post-training time, where the task is to compress a well-trained model using only a small set of calibration input data. In this work, we introduce a new low-rank approach to correct for quantization errors of \emph{activations} in LLMs: we propose to add low-rank weight matrices in full precision that act on the \emph{unquantized} activations. We then solve a joint optimization problem over the quantized representation of the weights and additional low-rank weight matrices to quantize both weights and activations. We focus on the case of 4-bit weight-and-activation quantization (W4A4). Using ranks equivalent to 10\% of the original weight matrix size, our approach reduces the accuracy gap with the original model by more than 50\%. Using ranks equivalent to 30\% of the original weight matrix, the accuracy gap is closed completely. We demonstrate our results on four recent LLMs, namely Llama-2, Llama-3, Phi-3 and Mixtral models.

Zero-Shot Learning of Causal Models

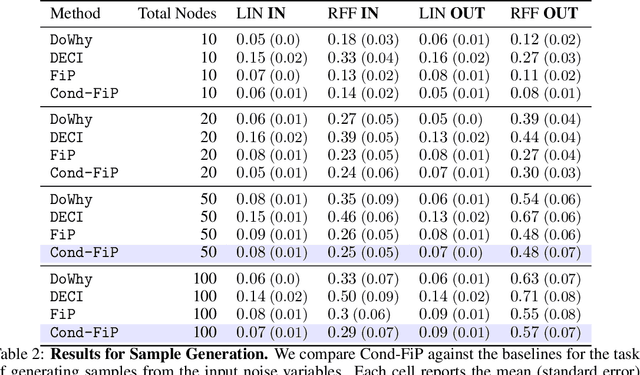
With the increasing acquisition of datasets over time, we now have access to precise and varied descriptions of the world, capturing all sorts of phenomena. These datasets can be seen as empirical observations of unknown causal generative processes, which can commonly be described by Structural Causal Models (SCMs). Recovering these causal generative processes from observations poses formidable challenges, and often require to learn a specific generative model for each dataset. In this work, we propose to learn a \emph{single} model capable of inferring in a zero-shot manner the causal generative processes of datasets. Rather than learning a specific SCM for each dataset, we enable the Fixed-Point Approach (FiP) proposed in~\cite{scetbon2024fip}, to infer the generative SCMs conditionally on their empirical representations. More specifically, we propose to amortize the learning of a conditional version of FiP to infer generative SCMs from observations and causal structures on synthetically generated datasets. We show that our model is capable of predicting in zero-shot the true generative SCMs, and as a by-product, of (i) generating new dataset samples, and (ii) inferring intervened ones. Our experiments demonstrate that our amortized procedure achieves performances on par with SoTA methods trained specifically for each dataset on both in and out-of-distribution problems. To the best of our knowledge, this is the first time that SCMs are inferred in a zero-shot manner from observations, paving the way for a paradigmatic shift towards the assimilation of causal knowledge across datasets.

FiP: a Fixed-Point Approach for Causal Generative Modeling

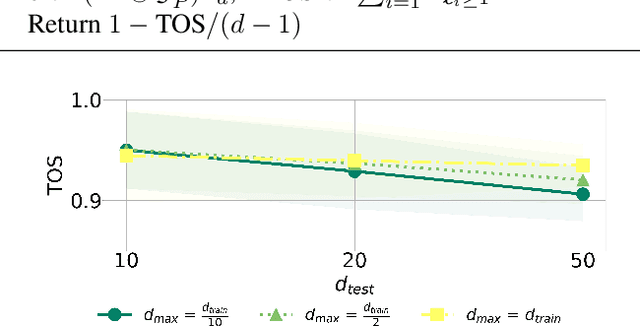
Modeling true world data-generating processes lies at the heart of empirical science. Structural Causal Models (SCMs) and their associated Directed Acyclic Graphs (DAGs) provide an increasingly popular answer to such problems by defining the causal generative process that transforms random noise into observations. However, learning them from observational data poses an ill-posed and NP-hard inverse problem in general. In this work, we propose a new and equivalent formalism that does not require DAGs to describe them, viewed as fixed-point problems on the causally ordered variables, and we show three important cases where they can be uniquely recovered given the topological ordering (TO). To the best of our knowledge, we obtain the weakest conditions for their recovery when TO is known. Based on this, we design a two-stage causal generative model that first infers the causal order from observations in a zero-shot manner, thus by-passing the search, and then learns the generative fixed-point SCM on the ordered variables. To infer TOs from observations, we propose to amortize the learning of TOs on generated datasets by sequentially predicting the leaves of graphs seen during training. To learn fixed-point SCMs, we design a transformer-based architecture that exploits a new attention mechanism enabling the modeling of causal structures, and show that this parameterization is consistent with our formalism. Finally, we conduct an extensive evaluation of each method individually, and show that when combined, our model outperforms various baselines on generated out-of-distribution problems.

The Essential Role of Causality in Foundation World Models for Embodied AI

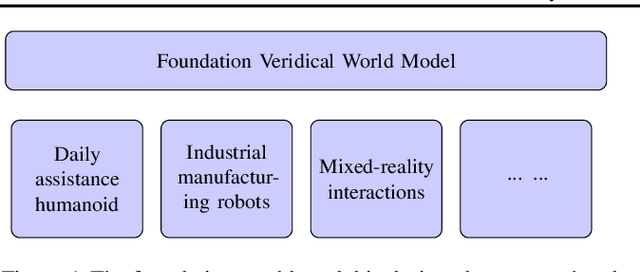
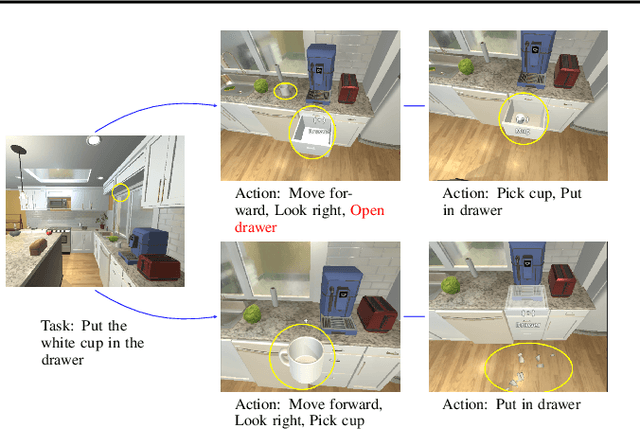
Recent advances in foundation models, especially in large multi-modal models and conversational agents, have ignited interest in the potential of generally capable embodied agents. Such agents would require the ability to perform new tasks in many different real-world environments. However, current foundation models fail to accurately model physical interactions with the real world thus not sufficient for Embodied AI. The study of causality lends itself to the construction of veridical world models, which are crucial for accurately predicting the outcomes of possible interactions. This paper focuses on the prospects of building foundation world models for the upcoming generation of embodied agents and presents a novel viewpoint on the significance of causality within these. We posit that integrating causal considerations is vital to facilitate meaningful physical interactions with the world. Finally, we demystify misconceptions about causality in this context and present our outlook for future research.

Robust Linear Regression: Phase-Transitions and Precise Tradeoffs for General Norms

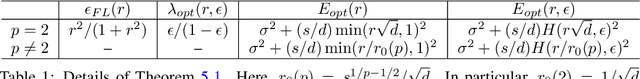
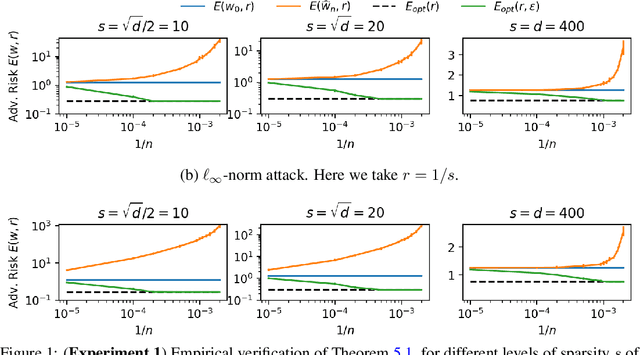
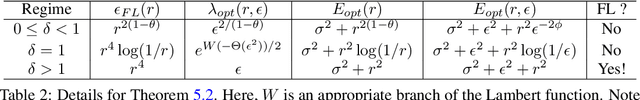
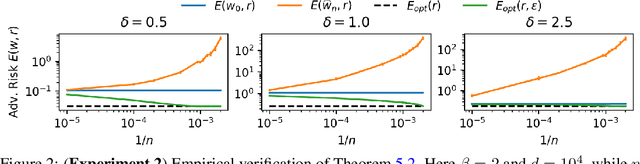
In this paper, we investigate the impact of test-time adversarial attacks on linear regression models and determine the optimal level of robustness that any model can reach while maintaining a given level of standard predictive performance (accuracy). Through quantitative estimates, we uncover fundamental tradeoffs between adversarial robustness and accuracy in different regimes. We obtain a precise characterization which distinguishes between regimes where robustness is achievable without hurting standard accuracy and regimes where a tradeoff might be unavoidable. Our findings are empirically confirmed with simple experiments that represent a variety of settings. This work applies to feature covariance matrices and attack norms of any nature, and extends beyond previous works in this area.

Unbalanced Low-rank Optimal Transport Solvers

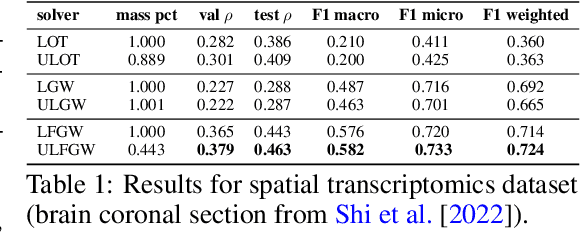
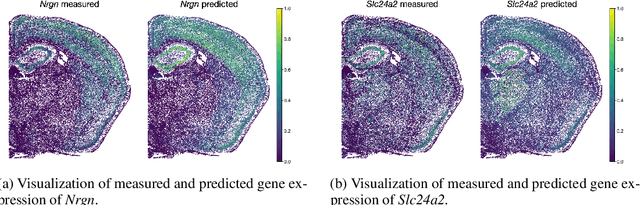
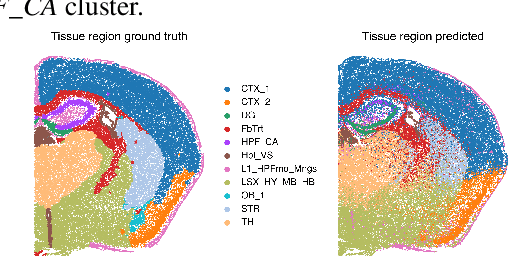
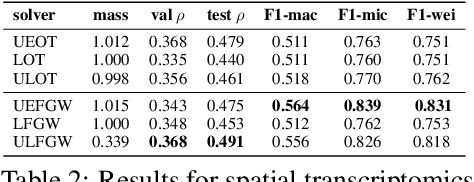
The relevance of optimal transport methods to machine learning has long been hindered by two salient limitations. First, the $O(n^3)$ computational cost of standard sample-based solvers (when used on batches of $n$ samples) is prohibitive. Second, the mass conservation constraint makes OT solvers too rigid in practice: because they must match \textit{all} points from both measures, their output can be heavily influenced by outliers. A flurry of recent works in OT has addressed these computational and modelling limitations, but has resulted in two separate strains of methods: While the computational outlook was much improved by entropic regularization, more recent $O(n)$ linear-time \textit{low-rank} solvers hold the promise to scale up OT further. On the other hand, modelling rigidities have been eased owing to unbalanced variants of OT, that rely on penalization terms to promote, rather than impose, mass conservation. The goal of this paper is to merge these two strains, to achieve the promise of \textit{both} versatile/scalable unbalanced/low-rank OT solvers. We propose custom algorithms to implement these extensions for the linear OT problem and its Fused-Gromov-Wasserstein generalization, and demonstrate their practical relevance to challenging spatial transcriptomics matching problems.