Zero-Shot Learning of Causal Models

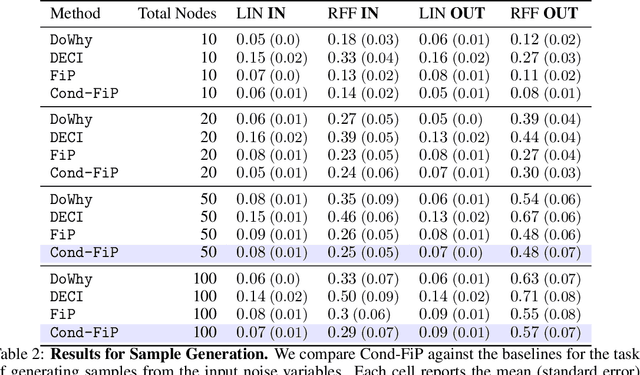
With the increasing acquisition of datasets over time, we now have access to precise and varied descriptions of the world, capturing all sorts of phenomena. These datasets can be seen as empirical observations of unknown causal generative processes, which can commonly be described by Structural Causal Models (SCMs). Recovering these causal generative processes from observations poses formidable challenges, and often require to learn a specific generative model for each dataset. In this work, we propose to learn a \emph{single} model capable of inferring in a zero-shot manner the causal generative processes of datasets. Rather than learning a specific SCM for each dataset, we enable the Fixed-Point Approach (FiP) proposed in~\cite{scetbon2024fip}, to infer the generative SCMs conditionally on their empirical representations. More specifically, we propose to amortize the learning of a conditional version of FiP to infer generative SCMs from observations and causal structures on synthetically generated datasets. We show that our model is capable of predicting in zero-shot the true generative SCMs, and as a by-product, of (i) generating new dataset samples, and (ii) inferring intervened ones. Our experiments demonstrate that our amortized procedure achieves performances on par with SoTA methods trained specifically for each dataset on both in and out-of-distribution problems. To the best of our knowledge, this is the first time that SCMs are inferred in a zero-shot manner from observations, paving the way for a paradigmatic shift towards the assimilation of causal knowledge across datasets.

High-bandwidth Close-Range Information Transport through Light Pipes

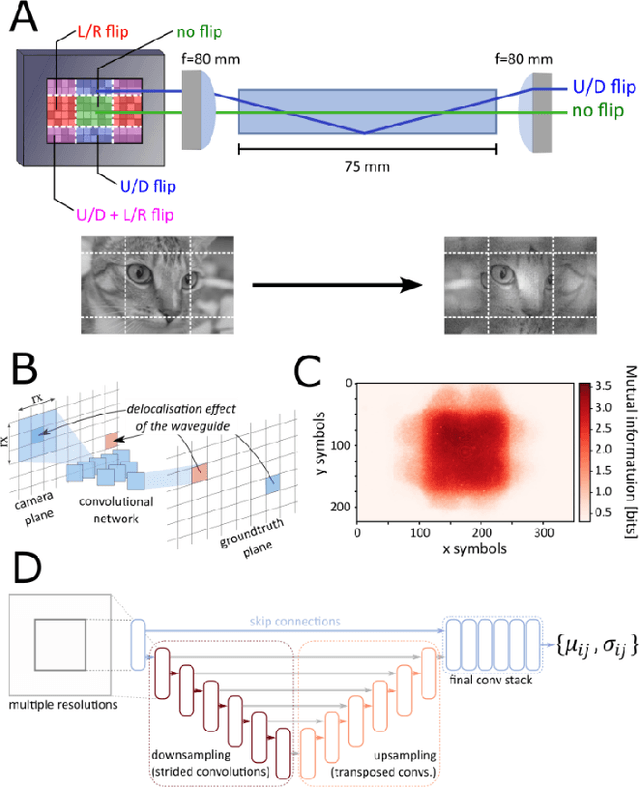
Image retrieval after propagation through multi-mode fibers is gaining attention due to their capacity to confine light and efficiently transport it over distances in a compact system. Here, we propose a generally applicable information-theoretic framework to transmit maximal-entropy (data) images and maximize the information transmission over sub-meter distances, a crucial capability that allows optical storage applications to scale and address different parts of storage media. To this end, we use millimeter-sized square optical waveguides to image a megapixel 8-bit spatial-light modulator. Data is thus represented as a 2D array of 8-bit values (symbols). Transmitting 100000s of symbols requires innovation beyond transmission matrix approaches. Deep neural networks have been recently utilized to retrieve images, but have been limited to small (thousands of symbols) and natural looking (low entropy) images. We maximize information transmission by combining a bandwidth-optimized homodyne detector with a differentiable hybrid neural-network consisting of a digital twin of the experiment setup and a U-Net. For the digital twin, we implement and compare a differentiable mode-based twin with a differentiable ray-based twin. Importantly, the latter can adapt to manufacturing-related setup imperfections during training which we show to be crucial. Our pipeline is trained end-to-end to recover digital input images while maximizing the achievable information page size based on a differentiable mutual-information estimator. We demonstrate retrieval of 66 kB at maximum with 1.7 bit per symbol on average with a range of 0.3 - 3.4 bit.

Digital phase-only holography using deep conditional generative models

Holographic wave-shaping has found numerous applications across the physical sciences, especially since the development of digital spatial-light modulators (SLMs). A key challenge in digital holography consists in finding optimal hologram patterns which transform the incoming laser beam into desired shapes in a conjugate optical plane. The existing repertoire of approaches to solve this inverse problem is built on iterative phase-retrieval algorithms, which do not take optical aberrations and deviations from theoretical models into account. Here, we adopt a physics-free, data-driven, and probabilistic approach to the problem. Using deep conditional generative models such as Generative-Adversarial Networks (cGAN) or Variational Autoencoder (cVAE), we approximate conditional distributions of holograms for a given target laser intensity pattern. In order to reduce the cardinality of the problem, we train our models on a proxy mapping relating an 8x8-matrix of complex-valued spatial-frequency coefficients to the ensuing 100x100-shaped intensity distribution recorded on a camera. We discuss the degree of 'ill-posedness' that remains in this reduced problem and compare different generative model architectures in terms of their ability to find holograms that reconstruct given intensity patterns. Finally, we challenge our models to generalise to synthetic target intensities, where the existence of matching holograms cannot be guaranteed. We devise a forward-interpolating training scheme aimed at providing models the ability to interpolate in laser intensity space, rather than hologram space and show that this indeed enhances model performance on synthetic data sets.